рефераты конспекты курсовые дипломные лекции шпоры

  • Раздел Математика
  •  / 
  • Метод решения неоднородного рекуррентного уравнения

Реферат Курсовая Конспект

Метод решения неоднородного рекуррентного уравнения

Метод решения неоднородного рекуррентного уравнения - раздел Математика, Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Рассмотрим Неоднородное Линейное Рекуррентное Уравнение ...

Рассмотрим неоднородное линейное рекуррентное уравнение

,

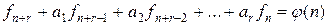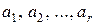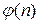n = 0, 1, 2, …, коэффициенты – это заданные постоянные, причём , а – заданная функция n. Для задания начальных условий фиксируем значения .

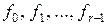Предположим, что одно решение уравнения найдено. Назовём это решение частным и обозначим через 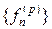. Положим

.

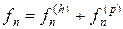Тогда: .

Так как второй член в левой части последнего равенства равен правой части, то

.

Это означает, что является решением однородного линейного рекуррентного уравнения, соответствующего 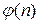= 0.

Таким образом, если найдено частное решение, то можно найти общее решение однородного рекуррентного уравнения. После чего по начальным условиям можно определить неопределённые коэффициенты. Для некоторых функций 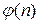частное решение можно найти достаточно просто. Так, в случае если , где – константа, то частным решением является

, (10.2)

где 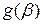– характеристический многочлен.

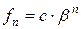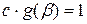Доказательство. Подставляя , где с – постоянная, в неоднородное рекуррентное уравнение, получаем . Таким образом: . Отсюда следует формула (10.2).

Пример 10.5. Найти решение уравнения 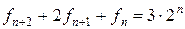с начальными условиями .

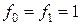Решение: Данное уравнение имеет характеристический многочлен . Если бы правая часть уравнения была равна , то частным решением было бы . Для соответствующее частное решение 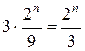. Общее решение равно:

.

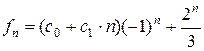По начальным условиям находим:

, , , ,

.

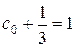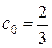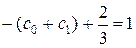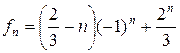Если 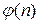является многочленом от n степени k

и единица не является характеристическим корнем рекуррентного уравнения, т.е. , то частное решение следует искать в виде:

.

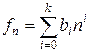Подставляя этот многочлен в неоднородное рекуррентное уравнение, получим:

.

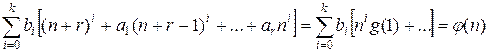Так как 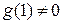, то, сравнивая коэффициенты при высших степенях в левой и правой частях последнего равенства, можно определить значение и далее последовательно коэффициенты .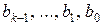

Пример 10.6. Найти решение уравнения с начальным условием .

Решение: Находим характеристический многочлен: 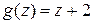; . Поскольку 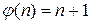, то k=1. Значит 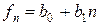. Записываем рекуррентное уравнение

.

Отсюда следует , .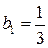

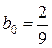Общее решение: 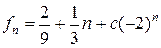. Из начального условия находим 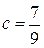и .

Развернуть
Открыть в широком формате

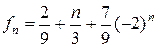– Конец работы –

Эта тема принадлежит разделу:

Лекция № 9. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Введение... Обыкновенные дифференциальные уравнения ОДУ не относятся к области дискретной математики Мы рассмотрим этот тип...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод решения неоднородного рекуррентного уравнения

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Операционное исчисление
Существуют различные способы решения дифференциальных уравнений. В данном разделе мы ознакомимся со способом, использующим операционное исчисление. Этот способ применяется к

Преобразование Лапласа
Хевисайд не дал строгого математического обоснования своего метода. Это было сделано позже с помощью интегрального преобразования Лапласа. В результате такого преобразования функция

Свойства изображений
· Если два изображения и

Изображения некоторых функций
1. Функция Хевисайда :

Основные теоремы операционного исчисления
В большинстве случаев применение операционного исчисления к решению задач укладывается в следующую схему. Пусть требуется найти некоторый результат в виде функции

Доказательство.
.   Теорема 9.7. (о свертке). Если

Доказательство теоремы о свертке.
  Пример 9.5.Применяя теорему о свертке, найти оригинал изображе

Производящая функция
Степенной ряд , коэффициентами которого являются элементы последовательности

Решение однородного рекуррентного уравнения
Однородное рекуррентное уравнение получается при j (n) = 0. Метод решения является обобщением решения предыдущего примера. Вначале производящая функция находится как рациональная функ

Дискретное преобразование Лапласа
Дискретное преобразование Лапласа применяют к так называемым решетчатым функциям. Решетчатой функцией

Основные теоремы дискретного преобразования Лапласа
1. Свойство линейности: . 2. Теорема сдвига:

Z-преобразование
Если ввести обозначение , то теорема сдвига примет следующую форму

Дискретная интерпретация операционного исчисления Микусиньского
Как известно, операционное исчисление, позволяющее сводить дифференциальные задачи к алгебраическим, возникло благодаря работам английского ученого Оливера Хевисайда (1859-1925), который предложил

Доказательство.
Все элементы матрицы равны нулю, за исключением одного. Это элемент в нижнем левом углу, который равен ед

Теоремы дискретного операционного исчисления
Теоремам непрерывного операционного исчисления можно поставить в соответствие теоремы дискретного операционного исчисления. Приведем несколько таких теорем. Теорема 11.7.

Теорема 11.8.
, (). (11.2

Теорема 11.9.
, (). (11.2

Применение дискретного операционного исчисления
Преимуществом дискретного операционного исчисления является то, что его можно использовать как численный метод, а не только как символьные преобразования. При этом оно опирается на хорошо отработан

Plot(Out), hold on
  Рис. 11.2   Как можно видеть, для решения задачи достат

Хотите получать на электронную почту самые свежие новости?
Education Insider Sample
Подпишитесь на Нашу рассылку
Наша политика приватности обеспечивает 100% безопасность и анонимность Ваших E-Mail
Реклама
Соответствующий теме материал
  • Похожее
  • Популярное
  • Облако тегов
  • Здесь
  • Временно
  • Пусто
Теги