Производящая функция

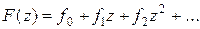Степенной ряд , коэффициентами которого являются элементы последовательности 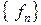, называется производящей функцией. Последовательность чисел однозначно определяет производящую функцию, но обратное утверждение верно не всегда. Если указанный степенной ряд сходится, то коэффициенты определяются по F(z) однозначно. Производящая функция отличается от z-преобразования только тем, что степени (при разложении этой функции в степенной ряд) положительны, в то время как у z-преобразования – они отрицательны. Простой заменой переменной можно преобразовать производящую функцию в z-преобразование. Поэтому для производящих функций справедливы все теоремы дискретного преобразования Лапласа.

Пусть 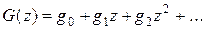– производящая функция последовательности чисел 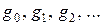, а a и b – произвольные фиксированные числа.

Поскольку , то последовательности отвечает производящая функция . Это соответствует свойству линейности преобразования Лапласа. Далее, если взять произведение производящих функций

,

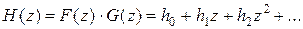то последовательность чисел может быть получена из последовательносте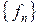й и 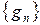с помощью соотношения

.

Последняя формула следует из теоремы о свертке двух решетчатых функций.

Пример 10.1. Найдем производящие функции последовательностей чисел {1} и {n}.

Решение: Последовательности {1} соответствует ряд:

.

Для доказательства необходимо левую и правую часть умножить на .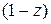

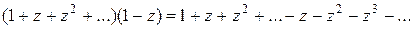
Последовательности чисел {n} соответствует ряд

.

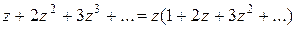Поскольку выражение в скобках в правой части равенства получается дифференцированием ряда , то оно равно производной от функции 1/(1 – z). Следовательно, правая часть равна

.

Следующая задача показывает, что производящие функции могут быть полезными при решении линейных рекуррентных уравнений.

Пример 10.2. Решить уравнение 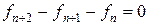(уравнение Фибоначчи) с начальными условиями .

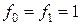Решение: Обозначим через F(z) производящую функцию последовательности чисел 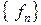. Умножая обе части рекуррентного уравнения на 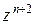, получим

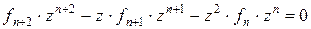, n = 0, 1, 2 …

Складывая эти равенства для всех n от 0 до ∞, имеем:

.

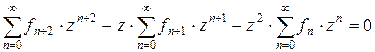Заметим, что первая сумма в левой части равенства равна разности функции F(z) и первых двух членов её разложения , вторая сумма равна разности F(z) и первого члена , а третья сумма равна F(z). Поэтому можем записать

[F(z) – (1 + z)] – z [F(z) – 1] – z² F(z) = 0.

Отсюда находим

,

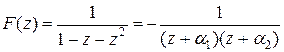где ; . В результате получим

.

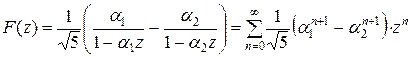Таким образом: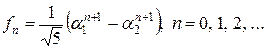

Члены последовательности, полученной в этой задаче, известны как числа Фибоначчи.