Последовательность независимых испытаний.

Пусть A есть некоторое случайное событие по отношению к некоторому опыту σ. Обозначим 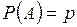; 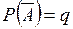, где 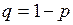. В качестве примера рассмотрим опыт, состоящий в бросании игрального кубика, а в качестве A возьмем случайное событие, состоящее в выпадении 6^и очков. Очевидно, что в этом примере ; .

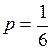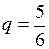Пусть опыт σ повторяется независимо n раз. В каждом испытании событие A может как наступить, так и не наступить. Обозначим через P_n(k) вероятность того, что при n независимых испытаниях событие A произойдет k раз, где k ≤ n.

Теорема(Бернулли).Имеет место формула.

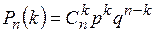. (1)

Определение. Формула (1) называется формулой Бернулли, а многократное повторение опыта σ, при каждом из которых может наступить с одной и той же вероятностью событие A называется схемой Бернулли.

Задача.Доказать формулу (1).

Пример. Вернемся к первому примеру. Пусть игральный кубик бросается 3 раза. Найти вероятность того, что шестерка выпадет 2 раза.

Ответ дается формулой (1), в которой , , , :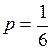

.

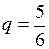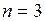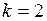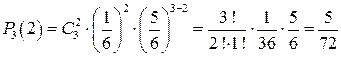Приведем еще две формулы, применяемые в задачах, связанных со схемой Бернулли.

Вероятность не наступления события A в течение n испытаний согласно формуле Бернулли равна

.

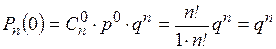Пусть B есть событие, состоящее в том, что в n опытах событие A ни разу не произойдет. Пусть C есть случайное событие, состоящее в том, что в n опытах событие A произойдет хотя бы один раз. Очевидно, что B и C образуют полную группу событий. Поэтому .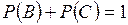

По доказанному

.

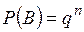Следовательно,

.

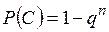Определение. Число k = k₀, при котором вероятность P_n(k) является наибольшей, называется наивероятнейшим числом наступления события A в n испытаниях.

Теорема.Есл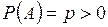и и 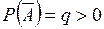, то число k₀ удовлетворяет двойному неравенству

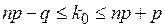. (2)

Замечание. Если 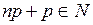, то имеются два наивероятнейших значения 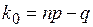и .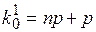

Пример. Игральный кубик бросается 20 раз. Каково наиболее вероятное число выпадений 6^и очков.

Решение.

В данном случае 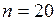, , 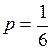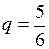. Вычислим 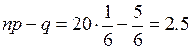; 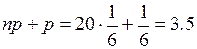. Поэтому 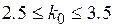. Так как 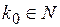, то 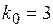. Следовательно, наиболее вероятное число выпаданий шестерки равно 3.

Замечание. Из последней теоремы следует, что одно из двух целых чисел (а иногда оба), ближайших к числу np, являются наиболее вероятным числом успехов. Число np допускает и другую важную интерпретацию. А именно, np можно рассматривать в определенном смысле как среднее число наступлений события A в n опытах. Этот факт точно формулируется и строго обосновывается в предельных теоремах теории вероятности.

2. Приближенные формулы для P_n(k) при больших значениях n и k.

 

Часто при решении задач приходится вычислять вероятности P_n(k) при больших значениях n и k, при которых вычисления по формуле Бернулли (1) сложно и громоздко. В этом случае используют приближенные формулы Муавра-Лапласса для случая, когда оба числа p и q не являются малыми. Приведем эти формулы.

Если n велико, то из локальной теоремы Муавра-Лапласса следует приближенная формула

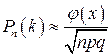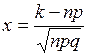, ,(3)

где .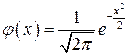

В конце пособия приведена таблица значений функции φ(x). Заметим, что φ(x) – четная функция, то есть φ(-x) = φ(x). Поэтому в таблице приводятся значения φ (x) только для положительных значений аргумента.

При больших n вероятности P_n(k) близки к 0. Поэтому на практике вычисляют вероятность попадания числа успехов в заданный промежуток.

Пусть k есть число наступлений события A в n опытах. Обозначим через P_n(k₁,k₂) вероятность того, что .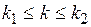

Если n велико, то из интегральной теоремы Муавра-Лапласса следует приближенная формула

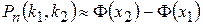, (4)

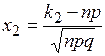где , , (5)

а 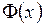есть функция Лапласса:

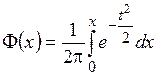. (6)

Таблица значений функции Ф приведена в конце пособия.

Перечислим без доказательства известные свойства функции Ф(x):

1. Ф(x) – нечетная функция.

2. Ф(x) – возрастает.

3. , .

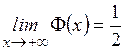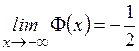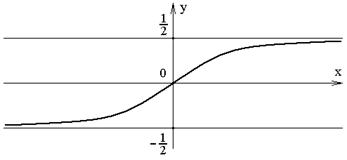
График функции y = Ф(x) изображен на рисунке

Пример. Вероятность поражения мишени стрелком равна 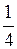. Какова вероятность того, что при 300 выстрелах мишень будет поражена.

а) ровно 72 раз; б) от 66 до 84 раз?

Решение.

В этом примере n = 300, p = 1.25, q = 1 – 0.25 = 1.75, k = 72. В соответствии с формулами (3) вычисляем

;

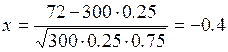По таблице значений φ (x) находим значение φ (–0,4) = φ (0.4) = 0.368. Тогда по формуле (3)

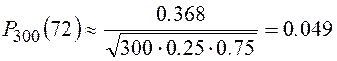
Далее по условию k₁ = 66, k₂ = 84. По формулам (5) вычислим

, .

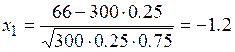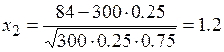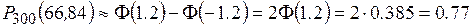
Значение функции 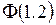найдено по таблице.

Замечание. Если одно из чисел p или q близко к 0, то значения P_n(k), вычисленные по приближенным формулам, сильно отличаются от точных значений. В этом случае рекомендуется использовать приближенную формулу Пуассона. Приведем эту формулу.

Пусть вероятность p мала. Тогда

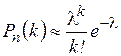, где .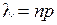

Тема 4: Случайные величины. Непрерывные и дискретные случайные величины. Закон распределения случайных дискретных величин. Бином распределения, распределение Пуассона.