рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Социология
- /
- Формулы комбинаторики.
Реферат Курсовая Конспект
Формулы комбинаторики.
Формулы комбинаторики. - раздел Социология, Классическое определение вероятности Комбинаторика - Это Раздел Математики, Основной Задачей ...
Комбинаторика - это раздел математики, основной задачей которой является подсчёт числа вариантов, возникающих в той или иной ситуации. При решении задач с использованием классического определения вероятности нам понадобятся некоторые формулы комбинаторики.
Размещения.
Определение 1. Размещением без повторений из n элементов по k называется всякое упорядоченное подмножество данного множества M={a1,a2,¼,an}, содержащее k элементов.
Отметим, что из определения сразу следует, что, во-первых, все элементы в размещении без повторений различны (в противном случае найдется два одинаковых элемента), во-вторых, k£ n, в-третьих, два различных размещения без повторений различаются либо составом входящих в них элементов, либо порядком их расположения. То есть порядок следования существенен.
Теорема 1. Число различных размещений без повторений из n элементов по k (k£ n) равно
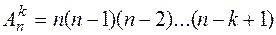 (4)
(4)
Доказательство.
Пусть M={a1,a2,¼,an}. Требуется определить число различных строк вида (x1,x2,¼,xk), где все элементы x1,x2,¼,xk ÎM и различны. Первый элемент x1 можно выбрать n способами. Если x1 уже выбран, то для выбора x2 осталось n-1 элементов. Аналогично, x3 можно выбрать n-2 способами и т.д. Последний элемент xk можно выбрать n-k+1 способами. Перемножая эти числа, получим формулу (4).Теорема доказана.
Пример 1. В классе 12 учебных предметов и в понедельник 5 разных уроков. Сколькими способами может быть составлено расписание занятий на понедельник?
Решение.
Число всевозможных вариантов расписания есть, очевидно, число различных размещений из 12 элементов по 5, то есть
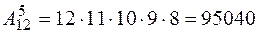
Важным частным случаем, является случай, когда n=k, то есть когда в строке (x1,x2,¼,xn) участвуют все элементы множества M. Строки без повторений, составленные из n элементов множества M называют перестановками из n элементов. Напомним, что в математике через n! обозначают произведение всех натуральных чисел от 1 до n, то есть 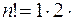 ¼
¼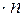 и по определению считают, что 0!=1.
и по определению считают, что 0!=1.
Следствие 1. Пользуясь формулой (4), находим, что число различных перестановок Pn из n элементов равно Pn = n!.
Определение 2. Размещением с повторениями из n элементов по k называется любая упорядоченная строка из k элементов множества M={a1,a2,¼,an}, некоторые из которых могут повторяться.
Например, слово “мама” есть размещение с повторениями из 2-х элементов M={м, а} по 4.
Теорема 2. Число различных размещений с повторениями из n элементов по k
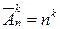 (5)
(5)
Доказательство.
Первый элемент в строку из k элементов может быть выбран n способами, поскольку |M|=n. Точно также 2-й, 3-й, …,k-й элементы могут быть выбраны n способами. Перемножая эти числа, получим
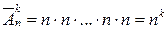
k раз
Теорема доказана.
Пример 2. Сколько можно составить различных двузначных чисел из цифр 1, 2, 3, 4, 5?
Решение.
В этой задаче M={1, 2, 3, 4, 5}, n=5, k=2.Поэтому ответом является число
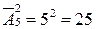
Пример 3. Сколькими способами k пассажиров могут распределиться по n вагонам, если для каждого пассажира существенным является только номер вагона, а не занимаемое им в вагоне место?
Решение.
Перенумеруем всех пассажиров. Пусть x1 - номер вагона, выбранного первым пассажиром, x2 - номер вагона второго пассажира, …, xk - номер вагона k-го пассажира. Строка (x1,x2,¼,xk) полностью характеризует распределение пассажиров по вагонам. Каждое из чисел x1,x2,¼,xk может принимать любое целое значение от 1 до n. Поэтому в этом примере
M={1, 2,…,n} и различных распределений по вагонам будет столько же, сколько строк длиной k можно составить из элементов множества M, то есть
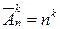 .
.
Отметим ещё раз, что в размещениях с повторениями и без повторений важен порядок следования элементов. Если порядок следования элементов не существенен, то в этом случае говорят о сочетаниях.
Сочетания(без повторения).
Определение 3.Пусть M={a1,a2,¼,an}.Любое подмножество X мно-жества M, содержащее k элементов, называется сочетанием k элементов из n.
Отметим сразу, что в этом определении порядок следования элементов множества X несущественен и, что k£n, поскольку k=½X½, n=½M½ и XÍM.
Теорема 3. Число различных сочетаний k элементов из n равно
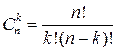 . (6)
. (6)
Доказательство.
Каждое сочетание k элементов из n порождает k! различных размещений без повторений из n по k с помощью различных перестановок (см. следствие 1). Таким образом, все 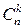 сочетаний из k элементов из n после различных k! перестановок порождают все
сочетаний из k элементов из n после различных k! перестановок порождают все 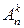 размещений без повторений из n по k. Поэтому
размещений без повторений из n по k. Поэтому 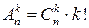 . Следовательно,
. Следовательно,
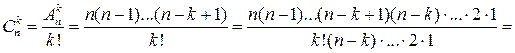
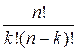 .
.
Теорема доказана.
Отметим, что в ходе доказательства мы получили ещё одно выражение для 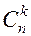 :
:
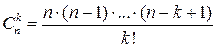 . (7)
. (7)
Пример 4. Сколько различных вариантов хоккейной команды можно составить из 9 нападающих, 5 защитников и 3 вратарей, если в состав команды должны войти 3 нападающих, 2 защитника и 1 вратарь?
Решение.
Трёх нападающих можно выбрать 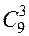 числом способов. Двух защитников из 5 можно выбрать
числом способов. Двух защитников из 5 можно выбрать 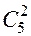 числом способов. Комбинируя каждую тройку нападающих с каждой парой защитников, получим
числом способов. Комбинируя каждую тройку нападающих с каждой парой защитников, получим 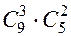 различных команд без вратаря. Комбинируя эти команды с каждым из 3-х вратарей, получим
различных команд без вратаря. Комбинируя эти команды с каждым из 3-х вратарей, получим 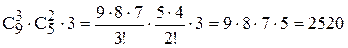 различных команд. (При вычислении
различных команд. (При вычислении 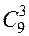 и
и 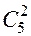 были использованы формулы 7).
были использованы формулы 7).
– Конец работы –
Эта тема принадлежит разделу:
Классическое определение вероятности
Классическое определение вероятности... Основные понятия... В жизни часто встречаются ситуации когда результат проводимого опыта испытания наблюдения нельзя предсказать...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Формулы комбинаторики.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов