Лабораторная работа № 11

 

ОПТИМИЗАЦИЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
МЕТОДОМ ДИХОТОМИИ

 

1. Цель работы

 

Изучить методику поиска с использованием ЭВМ экстремума функции одной переменной по схеме половинного деления.

 

2. Исходные данные

 

Целевая функция Z(X) и область допустимых значений аргумента

а<= X <=b принимаются по табл. 1 в соответствии с номером варианта. Погрешность определения оптимума Е = 0,001.

 

Таблица 1

Целевая функция и область допустимых

значений аргумента

 

N ВАРИ- АНТА	ЦЕЛЕВАЯ ФУНКЦИЯ	ОБЛАСТЬ ДОПУСТИМЫХ ЗНАЧЕНИЙ a<=X<=b
	Z=X4/4-2*X3+4.5*X2-3*X Z=X4/4-6*X2-8*X Z=X4/4+4*X3/3-6*X Z=X3/3+20*COS(X) Z=X3/3-SIN(Pi*X)/Pi Z=X3/3+COS(Pi*X)/Pi Z=X5/5+2.5*X2-3*X Z=1.1*X2-2X/Ln(2) Z=2X/Ln(2)-2*X3/3-X Z=2X/Ln(2)-2*X2 Z=2*X*Lg(X)-X2/4+0.1314*X Z=X5/5-X2-X Z=X6/6-2.5*X2+2*X Z=0.6*X3+0.1*COS(10*X)	3.1<=X<=5 -1.5<=X<=0 -2<=X<=-0.4 -1<=X<=1 -1<=X<= -0.1 -0.2<=X<=0.3 -2.5<=X<=-1.1 0<=X<=1.5 -0.3<=X<=0.2 0<=X=<=1 0.1<=X<=1.5 -1.5<=X<=0.5 -1.7<=X<= -1.2 -1<=X<= -0.4	0<=X<=0.8 2.5<=X<=4.5 0.1<=X<=2 1.5<=X<=4 0.1<=X<=0.8 0.5<=X<=1 0<=X<=1 1.8<=X<=3.5 5.5<=X<=7 2.8<=X<=5 3<=X<=5.5 1<=X<=2.5 1.1<=X<=1.5 -0.3<=X<=0.2

 

 

3. Содержание работы

 

3.1. Установить является экстремум функции минимумом или максимумом.

3.2. Разработать алгоритм и программу для определения экстремума функции методом дихотомии.

3.3. Рассчитать на ЭВМ оптимальное значение аргумента и соответствующее экстремальное значение функции. В процессе расчета печатать координаты граничных точек отрезка локализации экстремума.

3.4. Построить график целевой функции в пределах области допустимых значений аргумента.

 

4. Теоретические основы работы

 

Для определения вида экстремума функции Z(X) необходимо рас­считать значение первой производной в граничных точках отрезка [a, b]: Z' (a) и Z' (b). Если Z' (a)<0 и Z' (b)>0, то на отрезке [a, b] функция Z(X) имеет минимум , а если Z' (a)>0 и Z' (b)<0 - максимум.

Суть поиска экстремума функции методом дихотомии заключается в последовательном выполнении следующих операций: деление отрез­ка локализации экстремума на четыре равные части, определение экстремального среди значений целевой функции в полученных точках деления, выбор в качестве очередного отрезка локализации экстре­мума половины данного отрезка локализации, деление очередного отрезка локализации экстремума на четыре равные части и т.д. до получения требуемой точности результата.

Поиск минимума функции Y = f (X) методом дихотомии рекомен­дуется проводить по следующей схеме:

1) присвоить значения граничных точек отрезка [a, b]: X1 = а,

Х5 = b;

2) отрезок [X1, Х5] разделить пополам точкой ХЗ и вычислить значение функции в этой точке Y3 = f (X3);

3) точками Х2 и Х4 разделить на две части каждую половину отрезка [X1, Х5] и вычислить Y2 = f (X2) и Y4 = f (X4);

4) сравнить Y2 и Y3: если Y2 < Y3 (см. рис. 1 а), то исключить из рассмотрения отрезок [ХЗ, Х5], для чего присвоить значения Х5 = ХЗ, ХЗ = Х2, Y3 = Y2 и перейти к п.7;

5) если Y2 >= Y3, то сравнить Y3 и Y4: если Y4 < Y3

(см. рис. 1 б), то исключить отрезок [X1, ХЗ], для чего при­своить значения X1 = ХЗ, ХЗ = Х4, Y3 = Y4 и перейти к п.7;

6) если Y4 >= Y3 (см. рис. 1 в), то исключить отрезок [X1, Х2] и [Х4, Х5], выполнив присвоения X1 = Х2 и Х5 = Х4;

7) проверить условие окончания поиска Х5 - X1 <= Е, если условие не выполняется - перейти к п.З;

8) в случае окончания поиска оптимальное значение аргумента Х_о принять равным ХЗ и определить минимум функции

Y_min = f (X_o) = Y3

 

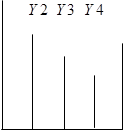Схема поиска минимума функции методом дихотомии.

 

Х1 Х2 Х3 Х4 Х5 Х1 Х2 Х3 Х4 Х5 Х1 Х2 Х3 Х4 Х5

 

Х1 Х3 Х5 Х1 Х3 Х5 Х1 Х3 Х5

а) б) в)

Рис. 1.

 

Если экстремум целевой функции Z(X) является минимумом, то рас­смотренная схема поиска применима непосредственно к заданной функ­ции, т.е. f (X) = Z(X). Если же функция Z(X) имеет максимум, то

для использования приведенной схемы поиска целевую функцию следует задавать с противоположным знаком, т.е. f (X) = -Z(X). Соответст­венно, при минимизации целевой функции полученный результат f (Xo) является ее минимумом Z_min = Y_min, а при максимизации найденное минимальное значение f (Xo) следует взять с противоположным знаком Z_max = -Y_min.

 

5. Содержание отчета

 

5.1. Цель работы

5.2. Исходные данные

5.3. Определение вида экстремума

5.4. Схема алгоритма оптимизации

5.5. Распечатка программы и результатов расчета

5.6. График целевой функции

5.7. Выводы