рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- X. Гипотезы о числовых характеристиках
Реферат Курсовая Конспект
X. Гипотезы о числовых характеристиках
X. Гипотезы о числовых характеристиках - раздел Философия, Эмпирические распределения случайной величины 1) Проверка Гипотезы ...
1) Проверка гипотезы 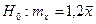
Выдвинем нулевую гипотезу и конкурирующую ей:
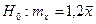

Из нормальной генеральной совокупности извлечена выборка объема  и по ней найдено среднее арифметическое значение
и по ней найдено среднее арифметическое значение 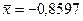 , дисперсия известна
, дисперсия известна 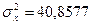 . Требуется по среднему арифметическому при уровне значимости
. Требуется по среднему арифметическому при уровне значимости  = 0,01; 0,05; 0,1 проверить нулевую гипотезу
= 0,01; 0,05; 0,1 проверить нулевую гипотезу 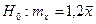 о равенствематематического ожидания
о равенствематематического ожидания  и значения
и значения 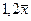 .
.
Наблюдаемое значение критерия вычислим по формуле:
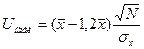 ,
,
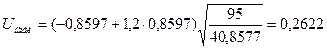
По таблице функции Лапласа [4] найдем критические точки для уровней значимости  = 0,01; 0,05; 0,1 по равенству:
= 0,01; 0,05; 0,1 по равенству:

Критические точки для уровней значимости  = 0,01; 0,05; 0,1 представлены в таблице 19.
= 0,01; 0,05; 0,1 представлены в таблице 19.
Таблица 19

| 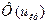
| 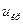
|
| 0,01 | 0,495 | 2,58 |
| 0,05 | 0,475 | 1,96 |
| 0,1 | 0,45 | 1,65 |
Получили, что для всех уровней значимости 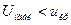 , следовательно, нет оснований отвергнуть нулевую гипотезу.
, следовательно, нет оснований отвергнуть нулевую гипотезу.
2) Проверка гипотезы 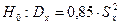
Выдвинем нулевую гипотезу и конкурирующую ей:
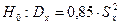
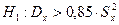
Из генеральной совокупности извлечена выборка объема  и по ней найдена несмещенная оценка дисперсии
и по ней найдена несмещенная оценка дисперсии 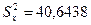 с
с 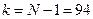 степенями свободы. Требуется по несмещенной оценке при уровне значимости
степенями свободы. Требуется по несмещенной оценке при уровне значимости  = 0,01; 0,05; 0,1 проверить нулевую гипотезу, состоящую в том, что дисперсия рассматриваемой выборки равна значению
= 0,01; 0,05; 0,1 проверить нулевую гипотезу, состоящую в том, что дисперсия рассматриваемой выборки равна значению 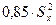 .
.
Критерий проверки нулевой гипотезы:
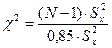
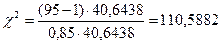
Так как конкурирующая гипотеза имеет вид 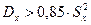 , поэтому критическая область правосторонняя. Критическую точку
, поэтому критическая область правосторонняя. Критическую точку 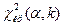 находим по таблице процентных точек распределения
находим по таблице процентных точек распределения 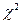 [1].
[1].
Критические точки для уровней значимости  = 0,01; 0,05; 0,1 представлены в таблице 20.
= 0,01; 0,05; 0,1 представлены в таблице 20.
Таблица 20

| 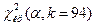
|
| 0,01 | 128,803 |
| 0,05 | 117,632 |
| 0,1 | 111,944 |
Так как 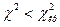 для всех уровней значимости
для всех уровней значимости  = 0,01; 0,05; 0,1, то нет оснований отвергнуть нулевую гипотезу.
= 0,01; 0,05; 0,1, то нет оснований отвергнуть нулевую гипотезу.
3) Проверка гипотезы 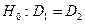
Выдвинем нулевую гипотезу и конкурирующую ей:
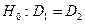
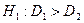
Заданы две выборки, которые были выбраны случайным образом преподавателем из исходных данных (см. задание на курсовую работу), без РВЗ:
Первая выборка  :
:
| 16,56 | 13,29 | -8 | -6,28 | -0,04 | 3,4 | 4,67 | -4,56 | 1,65 | 6,47 | -3,1 |
Вторая выборка 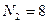 :
:
| -10,98 | 0,11 | -1,77 | 7,11 | -11,87 | -4,13 | -7,38 | -3,1 |
Генеральная совокупность, из которой извлечены независимые выборки с объемами  и
и 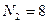 , распределена нормально. По данным выборкам определим несмещенные оценки дисперсии
, распределена нормально. По данным выборкам определим несмещенные оценки дисперсии 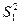 и
и 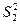 :
:
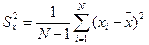
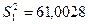
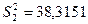
Требуется по несмещенным оценкам дисперсии при уровне значимости  = 0,01; 0,05; 0,1 проверить нулевую гипотезу, состоящую в том что дисперсии рассматриваемых совокупностей равны между собой.
= 0,01; 0,05; 0,1 проверить нулевую гипотезу, состоящую в том что дисперсии рассматриваемых совокупностей равны между собой.
В качестве критерия проверки нулевой гипотезы выступает отношение большей несмещенной оценки дисперсии к меньшей:
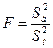
В нашем случае:
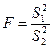

По таблице процентных точек F-распределения [1] по уровню значимости  и числам степеней свободы
и числам степеней свободы 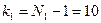 (число степеней свободы большей несмещенной оценки дисперсии),
(число степеней свободы большей несмещенной оценки дисперсии), 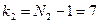 (число степеней свободы меньшей несмещенной оценки дисперсии) найдем критические точки
(число степеней свободы меньшей несмещенной оценки дисперсии) найдем критические точки 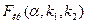 (см. таблицу 21).
(см. таблицу 21).
Таблица 21

| 
|
| 0,01 | 6,6201 |
| 0,05 | 3,6365 |
| 0,1 | 2,7025 |
Так как 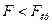 для всех уровней значимости
для всех уровней значимости  = 0,01; 0,05; 0,1, то нет оснований отвергнуть нулевую гипотезу.
= 0,01; 0,05; 0,1, то нет оснований отвергнуть нулевую гипотезу.
4) Проверка гипотезы 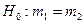
Выдвинем нулевую гипотезу и конкурирующую ей:
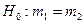
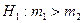
Заданы две выборки:
Первая выборка  :
:
| 16,56 | 13,29 | -8 | -6,28 | -0,04 | 3,4 | 4,67 | -4,56 | 1,65 | 6,47 | -3,1 |
Вторая выборка 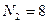 :
:
| -10,98 | 0,11 | -1,77 | 7,11 | -11,87 | -4,13 | -7,38 | -3,1 |
Найдем средние арифметические 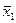 выборки, объем которой
выборки, объем которой  и
и 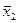 выборки, объем которой
выборки, объем которой 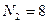 :
:
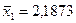
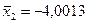
В качестве проверки нулевой гипотезы о равенстве математических ожиданий двух нормальных совокупностей с неизвестными, но одинаковыми дисперсиями (как показала проверка гипотезы об однородности дисперсий, сделанная в предыдущем пункте) необходимо вычислить наблюдаемое значение критерия:
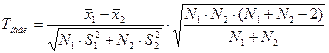 ,
,
при 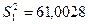 ,
, 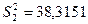 , которые были вычислены ранее.
, которые были вычислены ранее.
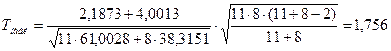
Так как конкурирующая гипотеза имеет вид 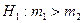 ,поэтому критическая область - правосторонняя, находим по таблице критических точек распределения Стьюдента [1] при уровне значимости
,поэтому критическая область - правосторонняя, находим по таблице критических точек распределения Стьюдента [1] при уровне значимости  = 0,01; 0,05; 0,1 критическую точку
= 0,01; 0,05; 0,1 критическую точку 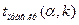 , где
, где 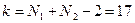 - число степеней свободы (см. таблицу 22).
- число степеней свободы (см. таблицу 22).
Таблица 22

| 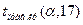
|
| 0,01 | 2,5669 |
| 0,05 | 1,7396 |
| 0,1 | 1,3334 |
Так как 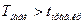 , то для уровней значимости
, то для уровней значимости  = 0,05; 0,1 нулевую гипотезу о равенстве математический ожиданий отвергаем, а для уровня значимости
= 0,05; 0,1 нулевую гипотезу о равенстве математический ожиданий отвергаем, а для уровня значимости  = 0,01 эту гипотезу принимаем, так как в этом случае
= 0,01 эту гипотезу принимаем, так как в этом случае 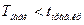 .
.
– Конец работы –
Эта тема принадлежит разделу:
Эмпирические распределения случайной величины
Предположение о виде закона распределения о РВЗ... На данном этапе анализа исходных данных по эмпирической функции распределения...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: X. Гипотезы о числовых характеристиках
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов