рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Решение
Реферат Курсовая Конспект
Решение
Решение - раздел Образование, МЕТОДИЧЕСКИЕ УКАЗАНИЯ Подынтегральную Функцию Можно Преобразовать, Понизив Степень:...
Подынтегральную функцию можно преобразовать, понизив степень:
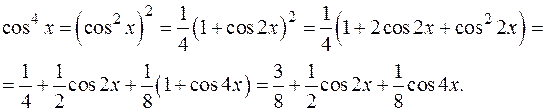
Поэтому
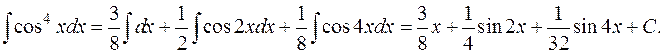
Рациональные функции и их интегрирование. Функция 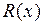 называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов
называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов 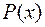 и
и 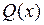 :
: 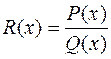 .
.
Пусть степень многочлена 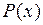 равна m, а степень
равна m, а степень 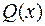 равна n, т. е:
равна n, т. е:
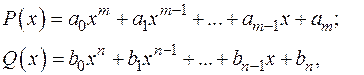
где 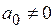 и
и 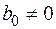 . Разделив числитель и знаменатель на число
. Разделив числитель и знаменатель на число 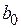 , мы получим, что коэффициент при старшей степени
, мы получим, что коэффициент при старшей степени 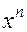 в знаменателе равен 1. Далее будет удобно предполагать, что эта операция уже произведена, то есть, что
в знаменателе равен 1. Далее будет удобно предполагать, что эта операция уже произведена, то есть, что 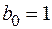 , и, что все коэффициенты
, и, что все коэффициенты 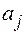 и
и 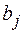 - вещественные числа. Если
- вещественные числа. Если 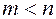 , то дробь
, то дробь 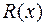 называется правильной, а если
называется правильной, а если 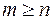 , то неправильной. Если дробь неправильная, то её числитель
, то неправильной. Если дробь неправильная, то её числитель 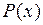 можно поделить на знаменатель
можно поделить на знаменатель 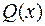 , получив при этом частное
, получив при этом частное 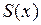 и остаток
и остаток 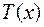 , степень которого
, степень которого 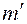 меньше n. Это означает, что
меньше n. Это означает, что 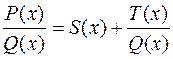 или что
или что 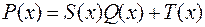 , где
, где 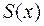 - некоторый многочлен, называемый целой частью рациональной дроби
- некоторый многочлен, называемый целой частью рациональной дроби 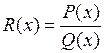 . Если остаток
. Если остаток 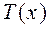 тождественно равен 0, то многочлен
тождественно равен 0, то многочлен 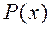 делится на
делится на 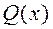 без остатка, и функция
без остатка, и функция 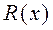 является многочленом, то есть совпадает со своей целой частью
является многочленом, то есть совпадает со своей целой частью 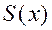 .
.
Предположим, что нам дана правильная рациональная дробь 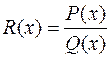 . Её знаменатель
. Её знаменатель 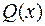 после разложения на множители может содержать множители следующих четырёх видов:
после разложения на множители может содержать множители следующих четырёх видов: 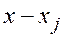 ;
; 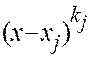 ,
,
где: 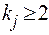 ;
; 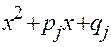 и
и 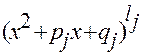 .
.
Каждому из указанных типов множителей знаменателя соответствуют простейшие рациональные дроби, а именно:
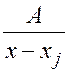 - простейшая дробь первого типа;
- простейшая дробь первого типа;
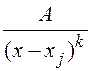 , где
, где 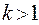 , - простейшая дробь второго типа;
, - простейшая дробь второго типа;
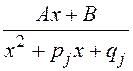 - простейшая дробь третьего типа;
- простейшая дробь третьего типа;
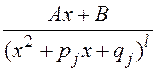 , где
, где 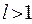 , - простейшая дробь четвёртого типа.
, - простейшая дробь четвёртого типа.
Здесь А и В - некоторые постоянные.
Любая правильная дробь 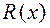 раскладывается в сумму простейших дробей указанных четырёх типов:
раскладывается в сумму простейших дробей указанных четырёх типов:
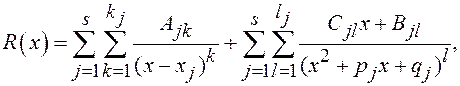
где 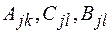 - некоторые постоянные. Эти постоянные отыскивают методом неопределённых коэффициентов.
- некоторые постоянные. Эти постоянные отыскивают методом неопределённых коэффициентов.
Для отыскания неизвестных постоянных методом неопределённых коэффициентов нужно, выписав разложение 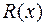 в сумму простейших дробей, привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен
в сумму простейших дробей, привести к общему знаменателю сумму, стоящую в правой части. Заметим, что этот общий знаменатель, очевидно, равен 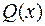 . Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями. Значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные
. Получим, что в левой и правой части равенства стоят дроби с одинаковыми знаменателями. Значит, и числители у них также тождественно равны. Числитель в правой части содержит неизвестные постоянные 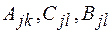 , а числитель в левой части - нет.
, а числитель в левой части - нет.
Далее, приравниваем друг к другу коэффициенты при одинаковых степенях х в числителях левой и правой частей: эти коэффициенты также совпадают вследствие тождественности числителей, при этом получаем систему линейных уравнений, которым должны удовлетворять неизвестные коэффициенты.
Пример. Разложить рациональную дробь 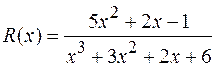 в сумму простейших дробей и вычислить
в сумму простейших дробей и вычислить 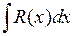 .
.
– Конец работы –
Эта тема принадлежит разделу:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
КУРГАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ... Кафедра Экономическая теория и моделирование экономических процессов...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов