рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Нтерполювання за Ньютоном
Реферат Курсовая Конспект
Нтерполювання за Ньютоном
Нтерполювання за Ньютоном - раздел Образование, Абсолютна і відносна похибки Недоліком Інтерполювання За Лагранжем Є Те, Що Якщо Для Поліп...
Недоліком інтерполювання за Лагранжем є те, що якщо для поліпшення наближення додати ще один вузол інтерполювання, доведеться всі обчислення проводити заново.
На практиці часто трапляються випадки, коли вузли інтерполяції стають відомими не одразу, а поступово, один за одним, наприклад, у процесі вимірювання. Тоді зручно побудувати процес інтерполювання у такий спосіб, щоб поява даних про новий вузол інтерполювання, призводила б до необхідності мінімального перерахунку попередніх обчислень. Саме таку властивість має інтерполювання за Ньютоном.
Нехай вузли інтерполяції рівновіддалені один від одного за аргументом, тобто виконується умова
 ; (
; ( ). (5.8)
). (5.8)
Різниці
 (5.9)
(5.9)
називають скінченними різницями першого порядку. Різниці сусідніх скінченних різниць першого порядку
 (5.10)
(5.10)
називають скінченними різницями другого порядку. Аналогічно
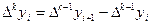 (5.11)
(5.11)
є скінченними різницями  -го порядку. Вони визначаються за формулою
-го порядку. Вони визначаються за формулою 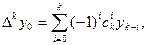 де
де  -біноміальні коефіцієнти.
-біноміальні коефіцієнти.
Розглянемо поліном
 . (5.12)
. (5.12)
Визначимо його коефіцієнти. Коефіцієнт  визначимо з умови проходження полінома через першу точку (
визначимо з умови проходження полінома через першу точку (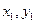 )
)
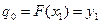 . (5.13)
. (5.13)
З умови проходження полінома через точку (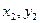 ) одержимо значення
) одержимо значення 
 ;
;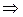
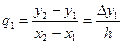 . (5.14)
. (5.14)
Аналогічно визначається решта коефіцієнтів
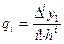 . (5.15)
. (5.15)
Підставляючи отримані вирази у (5.12), одержуємо
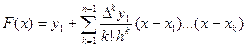 . (5.16)
. (5.16)
Це є перша інтерполяційна формула Ньютона (формула інтерполювання вперед).
Як бачимо, особливостями інтерполювання за Ньютоном є:
n при появі нового вузла додається лише новий член, решта не перераховується;
n коефіцієнти швидко зменшуються зі зростанням  , бо у знаменнику міститься факторіал від
, бо у знаменнику міститься факторіал від  .
.
Іноді використовується формула для інтерполювання назад
 .
.
Візьмемо деяку функцію f(x) R і систему вузлів інтерполяції
R і систему вузлів інтерполяції 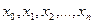 ,
,  ,
, 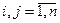 при і
при і j. Вузли інтерполяції не є рівновіддаленими. Для цієї функції і вузлів утворимо відношення
j. Вузли інтерполяції не є рівновіддаленими. Для цієї функції і вузлів утворимо відношення


 .
.
 Вони називаються розділеними різницями першого порядку. Одержавши їх, ми можемо утворити нові відношення
Вони називаються розділеними різницями першого порядку. Одержавши їх, ми можемо утворити нові відношення
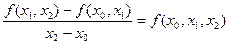
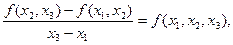 …,
…,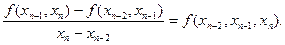
Вони називаються розділеними різницями другого порядку. Взагалі, якщо ми уже визначили розділені різниці k-го порядку 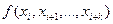 ,то розділені різниці (k+1)-го порядку знаходяться за допомогою формули
,то розділені різниці (k+1)-го порядку знаходяться за допомогою формули
 .
.
Іноді замість 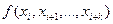 для позначення розділених різниць використовують позначення
для позначення розділених різниць використовують позначення 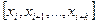 .
.
Домовимося розміщувати таблиці розділених різниць у такий спосіб:
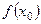
| |||
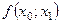
| |||
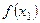
| 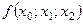
| ||

| 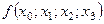
| ||

| 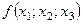
| ||

| 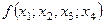
| ||

| 
| ||
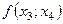
| |||
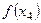
|
При 
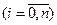 скінченні і розділені різниці пов'язані співвідношенням у вигляді
скінченні і розділені різниці пов'язані співвідношенням у вигляді
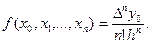
Розділені різниці порядку n від многочлена n-го степеня постійні, а різниці більш високого порядку дорівнюють нулю. Останнім зауваженням можна скористатися для виявлення помилок у таблицях многочленів чи функцій, близьких до них.
За допомогою розділених різниць можна побудувати інтерполяційний многочлен Ньютона
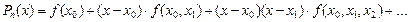
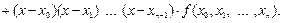
Варто зазначити, що при збільшенні кількості вузлів процес обчислення скінченних та поділених різниць стає все більш обчислювально нестійким - похибка визначення скінченних різниць великого порядку різко зростає зі збільшенням порядку скінченної різниці. Тому метод Ньютона може бути застосований лише для невеликої кількості вузлів.
5.2.3 Інтерполювання за Ермітом
У більш загальному випадку потрібно, щоб у вузлах інтерполяції збігалися не лише значення інтерполюючої функції і функції, яку необхідно інтерполювати, але й значення їхніх похідних до деякого порядку. У цьому випадку застосовують інтерполювання за Ермітом.
Інтерполяційним поліномом Ерміта 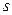 -го порядку називають поліном
-го порядку називають поліном 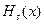 аргумента
аргумента 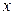 , який визначається з умов
, який визначається з умов
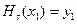 ;
;
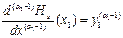 ;
;
 ;
; ;.
;. ;
;
. . . . . . . . . . . (5.17)
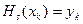 ;
;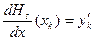 ;.
;.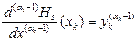 ;
;
. . . . . . . . . . .
 ;
; ;
;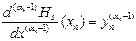 .
.
Тут, як і раніше,  - кількість вузлів інтерполяції.
- кількість вузлів інтерполяції.
Якщо у вузлі  поліном і функція, яка інтерполюється, збігаються до похідної порядку
поліном і функція, яка інтерполюється, збігаються до похідної порядку 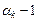 , то число
, то число 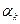 називається кратністю вузла
називається кратністю вузла 
 . При цьому
. При цьому 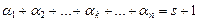 .
.
Інтерполяційний поліном Ньютона (5.12) узагальнюється на випадок кратних вузлів таким чином:
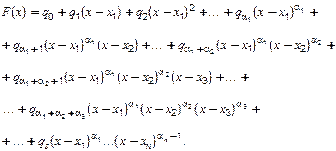 (5.18)
(5.18)
Інтерполювання за Ермітом зводиться до визначення 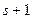 коефіцієнтів
коефіцієнтів  ,
,  , ...,
, ...,  з умов (5.17).
з умов (5.17).
5.2.4 Похибка інтерполяції та способи її зменшення
Зафіксуємо точку x та визначимо похибку інтерполяції rn(x)=f(x)-Pn(x). Нехай  та введемо функцію g(s)=f(s)-Pn(s)-kw(s), де w(s)=(s-x0)(s-x1)…(s-xn). При s=xi, i=0,1,…,n, w(xi)=0. Тому g(xi)=0, бо f(xi)=Pn(xi). Виберемо деяку точку x¹xi, i = 0,1,…,n та виберемо коефіцієнт k так, щоб g(x)=0. Тоді f(x)-Pn(x)-kw(x)=0; k=(f(x)-Pn(x))/w(x).
та введемо функцію g(s)=f(s)-Pn(s)-kw(s), де w(s)=(s-x0)(s-x1)…(s-xn). При s=xi, i=0,1,…,n, w(xi)=0. Тому g(xi)=0, бо f(xi)=Pn(xi). Виберемо деяку точку x¹xi, i = 0,1,…,n та виберемо коефіцієнт k так, щоб g(x)=0. Тоді f(x)-Pn(x)-kw(x)=0; k=(f(x)-Pn(x))/w(x).
Враховуючи, що w(n+1)(s) = (n+1)! та те, що g(s) має n+2 нулі на [a;b], то g'(s) має n+1 нуль, g''(s) має n нулів, …, g(n+1)(s) має принаймні один нуль. Нехай це буде при s=x. Тоді
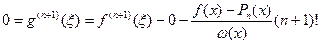 .
.
Звідси отримуємо оцінку для похибки інтерполювання
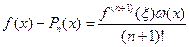 .
.
Тоді оцінка для абсолютної похибки поліноміальної інтерполяційної формули має вигляд
 . (5.19)
. (5.19)
Як бачимо з (5.19), похибка заміни функції 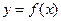 інтерполяційним многочленом залежить від вибору вузлів інтерполяції
інтерполяційним многочленом залежить від вибору вузлів інтерполяції  . Перш ніж перейти до питання про раціональний вибір вузлів інтерполяції, розглянемо деякі властивості одного з найважливіших і добре вивчених зараз класів спеціальних функцій – многочленів Чебишева першого роду, що часто використовуються для наближення функцій. Многочлен Чебишева
. Перш ніж перейти до питання про раціональний вибір вузлів інтерполяції, розглянемо деякі властивості одного з найважливіших і добре вивчених зараз класів спеціальних функцій – многочленів Чебишева першого роду, що часто використовуються для наближення функцій. Многочлен Чебишева  го степеня визначається за формулою
го степеня визначається за формулою
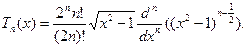 (5.20)
(5.20)
Для визначення многочленів Чебишева часто користуються тригонометричною формою запису
 , (5.21)
, (5.21)
що приводить до таких самих виразів для  , як і в (5.20).
, як і в (5.20).
Із тотожності 
при 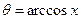 маємо рекурентну формулу
маємо рекурентну формулу
 .
.
Многочлен  має
має  коренів, які можна отримати, розв’язавши рівняння
коренів, які можна отримати, розв’язавши рівняння  , або
, або 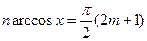 ;
;
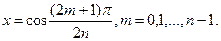 (5.22)
(5.22)
Як бачимо з (5.22), всі  коренів, що відповідають значенням
коренів, що відповідають значенням  знаходяться на відрізку [-1,1], причому ці точки не рівновіддалені, а згущуються ближче до кінця даного відрізка. З формули (5.21) також очевидно, що на відрізку [-1,1]
знаходяться на відрізку [-1,1], причому ці точки не рівновіддалені, а згущуються ближче до кінця даного відрізка. З формули (5.21) також очевидно, що на відрізку [-1,1]
 (5.23)
(5.23)
Доведено, що серед усіх можливих  значень
значень 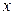 на відрізку
на відрізку 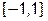 корені
корені  многочлена
многочлена  мають ту чудову властивість, що для них величина
мають ту чудову властивість, що для них величина
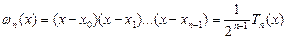 (5.24)
(5.24)
має найменше за модулем максимальне значення.
Беручи до уваги (5.24), запишемо
 . (5.25)
. (5.25)
Виходячи з властивостей коренів многочленів Чебишева першого роду і визначення інтерполяційного многочлена 
 -го степеня на відрізку
-го степеня на відрізку  можна стверджувати, що якщо за
можна стверджувати, що якщо за  вузлів інтерполювання взяти корені многочлена
вузлів інтерполювання взяти корені многочлена  то максимальне значення похибки на цьому відрізку буде найменшим для всіх можливих варіантів вибору
то максимальне значення похибки на цьому відрізку буде найменшим для всіх можливих варіантів вибору 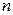 вузлів інтерполювання. Інтерполяційний многочлен, наділений такою властивістю, називається многочленом найкращого наближення. Оцінка (5.19) при цьому набирає вигляду
вузлів інтерполювання. Інтерполяційний многочлен, наділений такою властивістю, називається многочленом найкращого наближення. Оцінка (5.19) при цьому набирає вигляду
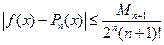 , де
, де  .
.
Якщо інтерполювання проводиться на довільному відрізку  , то заміною змінної
, то заміною змінної
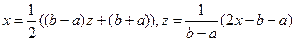
цей відрізок можна звести до відрізка 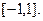 При цьому корені многочлена
При цьому корені многочлена  будуть знаходитися в точках
будуть знаходитися в точках
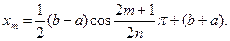
Оцінка похибки має вигляд
 .
.
5.2.5 Збіжність процесу інтерполяції
Розглянемо послідовність сіток
wn: a=x0<x1<…<xn-1 <xn=b.
Кажуть, що інтерполяційний поліном 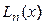 рівномірно збігається до заданої функції
рівномірно збігається до заданої функції  , якщо при max (x -xn-1) ® 0
, якщо при max (x -xn-1) ® 0 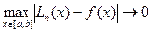 . Справедливі такі теореми.
. Справедливі такі теореми.
Теорема Фабера.Для будь-якої послідовності сіток wn знайдеться 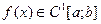 така, що збіжність відсутня.
така, що збіжність відсутня.
Теорема Марцинкевича.Для будь-якої функції 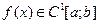 знайдеться послідовність сіток
знайдеться послідовність сіток 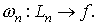
Приклад. Використовуючи інтерполяційний поліном Ньютона, визначити f(0.14), де y=f(x) задана таблично.
| x | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | |
| y | 0.1002 | 0.2013 | 0.8045 | 0.4108 | 0.5211 |
Розв’язання. Складаємо таблицю скінченних різниць, користуючись пакетом Excel:
| A | B | C | D | E | F | G | |
| x | y | 
| 
| 
| 
| 
| |
| =B3-B2 | =C3-C2 | =D3-D2 | =E3-E2 | =F3-F2 | |||
| 0,1 | 0,1002 | =B4-B3 | =C4-C3 | =D4-D3 | =E4-E3 | ||
| 0,2 | 0,2013 | =B5-B4 | =C5-C4 | =D5-D4 | |||
| 0,3 | 0,3045 | =B6-B5 | =C6-C5 | ||||
| 0,4 | 0,4108 | =B7-B6 | |||||
| 0,5 | 0,5211 |
У результаті отримаємо таке:
| A | B | C | D | E | F | G | |
| x | y | 
| 
| 
| 
| 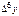
| |
| 0,1002 | 0,0009 | 0,0012 | -0,0002 | 0,0001 | |||
| 0,1 | 0,1002 | 0,1011 | 0,0021 | 0,0010 | -0,0001 | ||
| 0,2 | 0,2013 | 0,1032 | 0,0031 | 0,0009 | |||
| 0,3 | 0,3045 | 0,1063 | 0,0040 | ||||
| 0,4 | 0,4108 | 0,1103 | |||||
| 0,5 | 0,5211 |
Для розрахунку f(0.14) скористаємося інтерполяційним поліномом Ньютона, покладаючи, що x0=0.1 та h=0.1; тоді q=(x-x0)/h=(0,14-0,1)/0,1=0,4. Звідси за формулою визначаємо:
f(0.14)≈0,1002+0,1011*0,4+0,0021*0,4*(-0,6)/2+ +0,1010*0,4*(-0,6)*(-1,6)/6 ≈ 0,1405, або у MS Excel у даному випадку, формула матиме такий вигляд: =B3+Q*C3+Q*(Q-1)*D3/ФАКТР(2)+Q*(Q-1)*(Q-2)*
*E3/ФАКТР(3), де Q - адреса комірки із розрахованим значенням q.
При цьому похибка наближення дорівнює R4=|f(0.14)-P3(0.14)|<0.0001*0.4*0.6*1.6*2.6/4!= 4.16*10-6, або у MS Excel =ABS(F3*Q*(Q-1)*(Q-2)*(Q-3))/ФАКТР(4).
5.2.6 Інтерполяція за допомогою сплайнів
Підвищення точності інтерполювання вимагає збільшення вузлів інтерполяції. Це призведе до зростання степеня інтерполяційних многочленів. Але в умовах відсутності додаткової інформації про задану таблично функцію останні дають досить значну похибку. На практиці рідко проводять інтерполяцію поліномами степенів вище третього, тому що, по-перше, вони дають значні похибки й, по-друге, при нескінченному збільшенні порядку n інтерполяційного полінома Рn(х) послідовність Pn не є збіжною (відповідно до теореми Фабера). Цей факт уперше виявив Рунге в 1901 р. В цьому випадку більш ефективним є використання сплайнів, що на проміжку між вузлами інтерполювання є поліномами невисокого степеня. На всьому проміжку інтерполяції  сплайн - це функція, що склеєна з різних частин поліномів. Отже, розглянемо на відрізку
сплайн - це функція, що склеєна з різних частин поліномів. Отже, розглянемо на відрізку  систему вузлів
систему вузлів 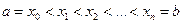 . Сплайном
. Сплайном  називається функція, що визначена на
називається функція, що визначена на  , має на ньому неперервні похідні
, має на ньому неперервні похідні 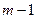 порядку і на кожному частковому відрізку
порядку і на кожному частковому відрізку 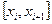 збігається з деяким многочленом степеня не вище
збігається з деяким многочленом степеня не вище 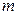 . При цьому хоча б на одному з відрізків степінь многочлена дорівнює
. При цьому хоча б на одному з відрізків степінь многочлена дорівнює 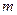 . Якщо
. Якщо  , маємо інтерполюючий сплайн. Визначити сплайн можна також так. Поліноміальним сплайном порядку m та дефекту k називається функція Sm,k(x) на сітці a=x0<x1<…<xn-1<xn=b така, що:
, маємо інтерполюючий сплайн. Визначити сплайн можна також так. Поліноміальним сплайном порядку m та дефекту k називається функція Sm,k(x) на сітці a=x0<x1<…<xn-1<xn=b така, що:
1) кожному проміжку 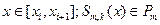 ;
;
2) число k називається дефектом сплайна, якщо 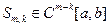 , 0<k<m;
, 0<k<m;
3) розглянемо сплайн дефекту 1. Sm,1 = Sm. Інтерполяційним сплайном називається Sm(x), якщо Sm(xi)=yi, i = 0, 1, …, n.
Лінійний інтерполяційний сплайн
Нехай 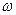 - розбиття відрізка
- розбиття відрізка 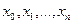 :
: 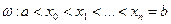 ,
, 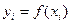 - задані значення.
- задані значення.
Сплайном першого степеня називається :неперервна на відрізку  , лінійна на кожному частковому проміжку функція f(x). Його позначення S1(x) . Нехай
, лінійна на кожному частковому проміжку функція f(x). Його позначення S1(x) . Нехай  . Вираз для сплайна S1(x) на цьому проміжку
. Вираз для сплайна S1(x) на цьому проміжку

 (5.26)
(5.26)
y
*
*
*
 *
*
 *
*
*
*
O 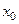

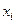

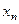
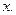
 |
Рис. – 5.1
Залишковий член такої інтерполяції 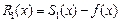 .
.
Оцінка залишкового члена залежить від диференціальних властивостей функції f(x).
Нехай  . Позначимо
. Позначимо 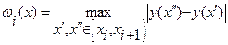 - коливання функції f(x) на проміжку
- коливання функції f(x) на проміжку 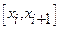 . Тоді використовується лема.
. Тоді використовується лема.
Лема (варіант теореми про середнє).
Нехай . Якщо величини
. Якщо величини  однакового знака, то існує точка
однакового знака, то існує точка  така, що
така, що 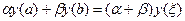 .
.
За допомогою цієї леми доводиться теорема про оцінку залишкового члена лінійного інтерполяційного сплайна.
Теорема. Якщо  , то
, то  . Дійсно,
. Дійсно,  , де
, де  . З наведеної вище леми маємо
. З наведеної вище леми маємо  , де
, де 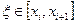 . Отже,
. Отже,
 .
.
З поліпшенням гладкості функції f(x) оцінка похибки її інтерполяції лінійними сплайнами також поліпшується. А саме, якщо 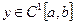 , то
, то  , де
, де 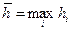 .
.
Для 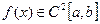 можна одержати оцінку
можна одержати оцінку  .
.
Подальше збільшення гладкості функції f(x) не дає підвищення порядку апроксимації. Відбувається насичення алгоритму.
Збіжність
Нехай на  задана послідовність сіток
задана послідовність сіток 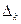 :
: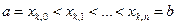 ,k=1,2,3…, які задовольняють умову
,k=1,2,3…, які задовольняють умову 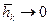 при
при 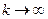 . Для
. Для 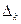 будується інтерполяційний сплайн
будується інтерполяційний сплайн 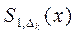 . Інтерполяційний процес вважається збіжним, якщо
. Інтерполяційний процес вважається збіжним, якщо  при
при 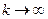 для будь-якої функції f(x) з деякого класу . Звідси випливає можливість інтерполяції з наперед заданою точністю
для будь-якої функції f(x) з деякого класу . Звідси випливає можливість інтерполяції з наперед заданою точністю
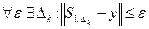 .
.
Перевага лінійних сплайнів у порівнянні з інтерполяційними многочленами полягає в тому, що з оцінки похибки випливає збіжність.
Нехай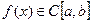 . За доведеною теоремою
. За доведеною теоремою  . За визначенням
. За визначенням  при
при 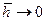 , тому процес інтерполяції лінійними сплайнами збігається на множині неперервних функцій по довільній послідовності сіток
, тому процес інтерполяції лінійними сплайнами збігається на множині неперервних функцій по довільній послідовності сіток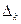 .
.
Якщо  , де k=1,2 , то похибка
, де k=1,2 , то похибка 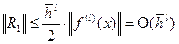 . Маємо збіжність інтерполяції порядку
. Маємо збіжність інтерполяції порядку  .
.
Кубічний інтерполяційний сплайн
Кубічні сплайн-функції моделюють дуже старий механічний пристрій, яким користувалися креслярі. Вони брали гнучкі рейки, виготовлені з досить пружного матеріалу, наприклад з дерева. Ці рейки закріплювали, підвішуючи важки в точках інтерполяції, що відповідають інтерполяційним вузлам. Рейка або механічний сплайн набирали форму з найменшою потенційною енергією. Остання умова має свій математичний вираз f(IV)(x) º 0. Якщо при цьому сплайн не руйнується, то тоді функція та її похідні повинні бути неперервними на [х0,хn] . З теорії балок відомо, що функція f(х) між кожною парою заданих точок може бути представлена поліномом 3-го степеня
f(x) = ai + bi(x - xi) + ci(x - xi)2 + di(x - xi)3,
де хi-1<х<хi. При цьому між кожною парою сусідніх вузлів поліноми з'єднуються неперервно (так само, як їх перші та другі похідні).
Інтерполяція кубічними сплайнами - це швидкий, ефективний і стійкий спосіб інтерполяції функцій, що є основним конкурентом поліноміальної інтерполяції. У його основу покладена така ідея - інтервал інтерполяції розбивається на невеликі відрізки, на кожному з яких функція задається поліномом третього степеня. Коефіцієнти полінома підбираються так, що на границях інтервалів забезпечується неперервність функції, її першої та другої похідних. Також є можливість задати граничні умови - значення першої або другої похідних на границях інтервалу. Якщо значення однієї з похідних на границі відомі, то задавши їх, ми одержуємо вкрай точну інтерполяційну схему. Якщо значення невідомі, то можна задати другу похідну на границі, що дорівнює нулю, й одержати досить гарні результати.
Кубічну сплайн-функцію, що задовольняє умови f"(х1)=f"(хn)=0, називають природним кубічним сплайном. З математичної точки зору було доведено [Алберг, 1972], що вона є єдиною функцією з мінімальною кривизною серед усіх функцій, що інтерполюють функцію в заданих точках та мають квадратично інтегровану другу похідну. У цьому змісті кубічний сплайн буде самою гладкою функцією, що інтерполює задані точки.
Побудова кубічного сплайна - простий і чисельно стійкий процес. Для  треба визначити 4 коефіцієнти для кожного проміжку
треба визначити 4 коефіцієнти для кожного проміжку  , тобто 4n параметрів. Вимагається щоб у внутрішніх вузлах сплайн і його похідні до 2-го порядку були неперервними
, тобто 4n параметрів. Вимагається щоб у внутрішніх вузлах сплайн і його похідні до 2-го порядку були неперервними
 , i=1,…,n-1; r=0,1,2.
, i=1,…,n-1; r=0,1,2.
Це дає 3n-3 умови для визначення параметрів, ще n+1 умова міститься у вимозі S3(xi) = yi, i=0,1,…,n.. Разом маємо 4n-2 умови. Ще 2 умови, необхідні для однозначного визначення коефіцієнтів сплайна, як правило, задаються у вигляді граничних умов, тобто умов у точках a й b. Розглянемо природні граничні умови  .
.
Позначивши 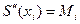 та враховуючи її лінійність, одержуємо
та враховуючи її лінійність, одержуємо
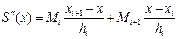 ,
, 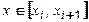 . (5.27)
. (5.27)
Двічі інтегруючи (5.27), одержуємо
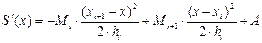 , (5.28)
, (5.28)
 , (5.29)
, (5.29)
де А та B- постійні інтегрування. Вищезгадані умови дають
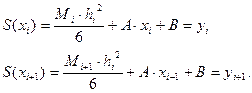 (5.30)
(5.30)
З них одержуємо

Підставляючи A та B в (5.29), одержуємо
 (5.31)
(5.31)
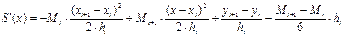 . (5.32)
. (5.32)
З (5.28) знаходимо значення однобічних похідних для вузла xi, i=1,2,…,n-1
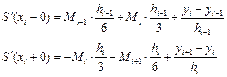 (5.33)
(5.33)
Вимагаючи неперервності 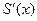 у вузлі xi одержуємо
у вузлі xi одержуємо
 , де i=1,…,n-1. (5.34)
, де i=1,…,n-1. (5.34)
Отже, отримуємо систему рівнянь відносно Mi вигляду
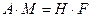 (5.35)
(5.35)
із квадратною матрицею A

і квадратною матрицею Н
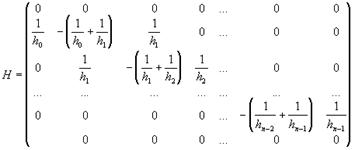 .
.
Координатами вектора F є значення y0,y1,…,yn.
Для матриці A ненульові елементи розміщені на головній діагоналі й двох сусідніх з нею. Такі матриці називаються тридіагональними. Для невиродженої матриці A виконана умова діагональної переваги 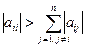 . Отже, система (5.35) однозначно розв'язувана, тобто існує єдиний кубічний інтерполяційний сплайн.
. Отже, система (5.35) однозначно розв'язувана, тобто існує єдиний кубічний інтерполяційний сплайн.
Вигляд граничних умов змінює деякі елементи матриці A, але в кожному разі вона залишається матрицею з діагональною перевагою. Розв’язок системи (5.35) із тридіагональною матрицею A може бути знайдений методом прогонки.
Випадки використання кубічного сплайна
При побудові інтерполяційного кубічного сплайна найчастіше використовуються граничні (крайові) умови трьох типів. Вибір граничних (крайових) умов є однією з центральних проблем при інтерполяції функцій. Він особливо важливий за необхідності забезпечити високу точність апроксимації функції  сплайном
сплайном  поблизу кінців відрізка
поблизу кінців відрізка  . Граничні значення суттєво впливають на поведінку сплайна
. Граничні значення суттєво впливають на поведінку сплайна  поблизу точок а та b. Цей вплив швидко слабшає при відході від них.
поблизу точок а та b. Цей вплив швидко слабшає при відході від них.
Отже, якщо 
 (
( ),
),  , то кубічний сплайн на цьому відрізку можна представити формулою
, то кубічний сплайн на цьому відрізку можна представити формулою
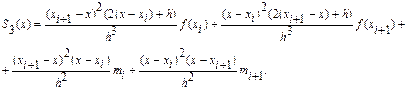 Тут
Тут 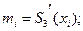
 . Для їх визначення накладають умови неперервності другої похідної в точках
. Для їх визначення накладають умови неперервності другої похідної в точках  та обмеження на значення сплайна і його похідних на кінцях проміжку
та обмеження на значення сплайна і його похідних на кінцях проміжку  - крайові умови. Тобто потрібна додаткова інформація про функцію, для якої є потреба в інтерполюванні.
- крайові умови. Тобто потрібна додаткова інформація про функцію, для якої є потреба в інтерполюванні.
Якщо на кінцях відрізка  відомі значення 1-ї похідної
відомі значення 1-ї похідної 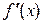 , то природно скористатися граничними (крайовими) умовами 1-го типу.
, то природно скористатися граничними (крайовими) умовами 1-го типу.
1 Граничні (крайові) умови 1-го типу. Якщо відомо, що  , то для визначення
, то для визначення 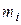 маємо систему рівнянь
маємо систему рівнянь
 (5.36)
(5.36)
Якщо на кінцях відрізка  відомі значення 2-ї похідної
відомі значення 2-ї похідної 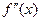 , то природно скористатися граничними (крайовими) умовами 2-го типу.
, то природно скористатися граничними (крайовими) умовами 2-го типу.
2 Граничні (крайові) умови 2-го типу. Якщо відомо
 , то є система рівнянь
, то є система рівнянь
 . (5.37)
. (5.37)
Якщо є можливість вибору між граничними (крайовими) умовами 1-го та 2-го типів, то перевагу потрібно надати умовам 1-го типу.
У випадку, коли ніякої додаткової інформації про поведінку апроксимованої функції немає, часто використовують так звані природні граничні (крайові) умови  .
.
Однак варто мати на увазі, що при такому виборі граничних (крайових) умов точність апроксимації функції  сплайном
сплайном  поблизу кінців відрізка
поблизу кінців відрізка  різко знижується. Іноді користуються граничними (крайовими) умовами 1-го або 2-го типу, але не з точними значеннями відповідних похідних, а з їх різницевими апроксимаціями. Точність такого підходу невисока.
різко знижується. Іноді користуються граничними (крайовими) умовами 1-го або 2-го типу, але не з точними значеннями відповідних похідних, а з їх різницевими апроксимаціями. Точність такого підходу невисока.
Практичний досвід розрахунків показує, що в такій ситуації найбільш доцільним є вибір природних граничних ( крайових) умов. Якщо  - періодична функція, то потрібно зупинитися на граничних (крайових) умовах 3-го типу.
- періодична функція, то потрібно зупинитися на граничних (крайових) умовах 3-го типу.
3 Граничні (крайові) умови 3-го типу. Якщо  - періодична функція
- періодична функція 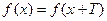 , то
, то  і система рівнянь має вигляд
і система рівнянь має вигляд
 . (5.38)
. (5.38)
Прикладреалізації алгоритмів інтерполяції функцій на псевдокоді
//розв’язує СЛАР методом Гауса
//M – матриця системи і вільні члени
//X – вектор відповідей
//n – кількість невідомих
linequ(M,n,e,X):
//доступна в модулі naz.pas
– Конец работы –
Эта тема принадлежит разделу:
Абсолютна і відносна похибки
С... Розділ Основні проблеми чисельного розв язання Класифікація похибок...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Нтерполювання за Ньютоном
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов