Метод Гауcа

 

Цей метод базується на приведенні шляхом еквівалентних перетворень вихідної системи (3.1) до вигляду з верхньою трикутною матрицею.

с₁₁x₁ + c₁₂x₂ + … + c_1nx_n = d₁

0 + c₂₂x₂ + … + c_2nx_n = d₂

................................................ (3.3)

0 + … 0+ c_n-1,n-1x_n-1 + c_n-1,nx_n = d_n-1

0 + 0 + +0 + c_nnx_n = d_n

Тоді з останнього рівняння відразу визначаємо 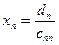. Підставляючи його в попереднє рівняння, знаходимо x_n-1 і т.д. Загальні формули для отримання розв’язку мають вигляд

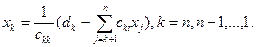(3.4)

При обчисленнях за формулами (3.4) треба буде виконати приблизно 1/2n² арифметичних дій. Зведення системи (3.1) до вигляду (3.3) можна виконати, послідовно заміняючи рядки матриці системи їх лінійними комбінаціями. Перше рівняння не змінюється. Віднімемо з другого рівняння системи (3.1) перше, помножене на таке число, щоб звернувся в нуль коефіцієнт при x₁. Потім у такий самий спосіб віднімемо перше рівняння з третього, четвертого і т.д. Таким чином обнуляються всі коефіцієнти першого стовпця, що лежать нижче головної діагоналі. Потім за допомогою другого рівняння виключимо з третього, четвертого і т.д. рівнянь коефіцієнти другого стовпця. Послідовно продовжуючи цей процес, виключимо з матриці всі коефіцієнти, що лежать нижче головної діагоналі.

Запишемо загальні формули процесу. Нехай проведене виключення коефіцієнтів з k-1 стовпця. Тоді залишилися такі рівняння з ненульовими елементами нижче головної діагоналі:

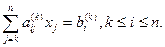(3.5)

Помножимо k-й рядок на число

(3.6)

і віднімемо від m-го рядка. Перший ненульовий елемент цього рядка звернеться в нуль, а інші зміняться за формулами

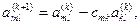(3.7)

.

Виконуючи обчислення при всіх зазначених індексах, виключимо елементи k-го стовпця. Будемо називати таке виключення циклом процесу. Виконання всіх циклів називається прямим ходом виключення.

Після виконання всіх циклів утвориться система, матриця якої має трикутний вигляд . Її легко розв’язати зворотним ходом за формулами (3.4).

Виключення за формулами (3.7) не можна проводити, якщо в ході розрахунків на головній діагоналі виявиться нульовий елемент 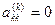Але в першому стовпці проміжної системи (3.5) всі елементи не можуть бути нулями: це означало б, що detA=0. Перестановкою рядків можна перемістити ненульовий елемент на головну діагональ і продовжити розрахунки.

Для зменшення обчислювальної похибки можна кожне повторення зовнішнього циклу починати з вибору максимального за модулем елемента в k-му стовпці (головного елемента) і перестановки рівняння з головним елементом так, щоб він виявився на головній діагоналі. Цей варіант називається методом Гауса з вибором головного елемента.

Однією з характеристик ефективності того чи іншого алгоритму вважають обчислювальні витрати, що визначаються кількістю елементарних операцій, які необхідно виконати для одержання розв’язку. Для прямого ходу методу Гауса число арифметичних операцій, відповідно до (3.6), (3.7), становить

Для зворотного ходу за формулами (3.4) число арифметичних операцій дорівнює

Загальні обчислювальні витрати методу Гауса становлять

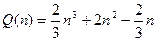, тобто .

Зауваження 1. Якщо елементи будь-якого рядка матриці системи в результаті перетворень стали дорівнювати нулю, то СЛАР – несумісна, оскільки не виконуються умови теореми Кронекера-Капеллі.

Зауваження 2. Якщо елементи будь-якого рядка матриці системи і права частина в результаті перетворень стали дорівнювати нулю, то СЛАР сумісна, але має безліч розв’язків, які можна отримати за допомогою методу Гауса для СЛАР порядку , де - ранг матриці заданої СЛАР.

3.2 Додаткові застосування методу Гауса

 

Виконання прямого ходу методу Гауса дозволяє також обчислити значення визначника матриці системи.

При заміні рядків матриці їхніми лінійними комбінаціями значення визначника не змінюється. Знак змінюється при кожній перестановці рядків. Для трикутної матриці величина визначника дорівнює добутку елементів, що стоять на головній діагоналі. Тому визначник обчислюється за формулою

.

Метод Гауса може бути використаний для отримання оберненої матриці.Позначимо її елементи через a_jm. Тоді співвідношення AA^-1=E можна записати так:

.

Якщо розглядати j-й стовпець оберненої матриці як вектор, то він є розв’язком лінійної системи вигляду (3.1) з матрицею A і спеціальною правою частиною (у якій на j-му місці стоїть одиниця, а на інших нулі). Таким чином, для обертання матриці треба розв’язати n систем лінійних рівнянь з однаковою матрицею A і різними правими частинами. Зведення матриці A до трикутної виконується при цьому тільки один раз, а праві частини перетворюються за формулами (3.6)-(3.7).

Перетворення матриці вимагає порядку 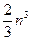операцій. Дії з перетворення правих частин систем і зворотний хід методу Гауса повторюються 7n разів, а однократне перетворення правих частин і зворотний хід вимагають порядку 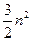операцій. Отже, сумарні обчислювальні витрати на пошук оберненої матриці становлять: .

Обертання матриці зводиться до розв’язання n систем лінійних рівнянь, але вимагає лише приблизно втроє більше дій, ніж розв’язання однієї системи рівнянь. Це обумовлюється тим, що при розв’язку лінійної системи велика частина обчислень пов'язана з приведенням матриці до трикутного вигляду, а це при обертанні матриці робиться тільки один раз. Зворотний хід і перетворення правих частин виконуються набагато швидше.