Процес Ейткена

Метод розрахунків на декількох сітках застосовується для підвищення порядку точності і в тому випадку, коли невідомий порядок головного члена похибки. Він має назву процесу Ейткена. Нехай

,

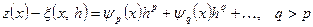але - невідоме. Проводяться обчислення на трьох сітках з кроками

.

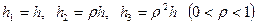Нехтуючи членами порядку , дістаємо

.

Звідси знаходимо . Далі можна скористатися вже відомим методом Рунге, який можна трактувати таким чином. Утворимо комбінацію 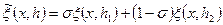і виберемо так, щоб

.

Дістанемо , причому

.

 

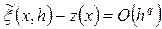Питання і завдання до розділу 6

 

1 Формули , які можна використати для чисельного диференціювання функції, що задана таблично.

2 Апріорна оцінка похибки чисельного диференціювання.

3 Апостеріорна оцінка похибки чисельного диференціювання.

4 Екстраполяція за Річардсоном в чисельному диференціюванні.

5 Скласти таблицю наближених значень похідної функції за таблицею її значень

x		1.1	1.2	1.3
y		2. 144	2. 297	2. 462

6 Переконатися в тім, що формула чисельного диференціювання 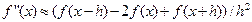має другий порядок точності.

7 Вивести формули чисельного диференціювання на основі лінійної інтерполяції.

8 Функція задана таблично

х
у	1.34	3.05	5.21	7.22	9.11	12.34

Обчислити .

 

Розділ 7

Чисельне інтегрування функцій

 

Задача чисельного інтегрування функції полягає в обчисленні наближеного значення визначеного інтеграла

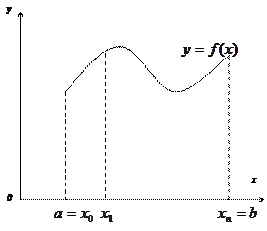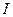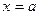з використанням значень підінтегральної функції у вузлах сітки . Визначений інтеграл представляє площу криволінійної трапеції, обмеженої кривою у=, віссю та прямими та .

Рис. – 7.1

У практичних розрахунках нерідко виникає потреба в обчисленні визначених інтегралів вигляду

,

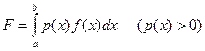де функція 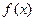та вагова функція неперервні на відрізку .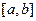

До чисельного інтегрування вдаються тоді, коли інтеграл неможливо виразити через елементарні функції або ж функція 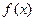задана таблично, а також коли внаслідок інтегрування одержано незручний для використання вираз. Тоді 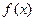наближають більш зручною функцією .

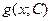Найчастіше підінтегральну функцію 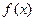заміняють на деякий узагальнений поліном. Тоді внаслідок лінійності такої апроксимації функцію 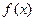можна записати так:

,

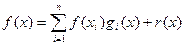де 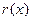- залишковий член апроксимації. Підставивши вираз 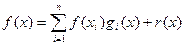у формулу , одержимо загальну формулу чисельного інтегрування – квадратурну формулу

,

де вузли; - ваги; похибка або залишковий член квадратурної формули.

Отже, інтеграл наближено замінено на суму, подібну до інтегральної, причому як вузли, так і коефіцієнти (ваги) квадратурної формули не залежать від функції .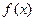

Будемо будувати формулу чисельного інтегрування за правилом .

Це відношення називається квадратурною формулою. При цьому: права частина виразу називається квадратурною сумою. Тут параметри квадратурної формули:квадратурні (вагові) коефіцієнти;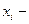квадратурні вузли.

Якщо межі інтегрування являються квадратурними вузлами, то отримуємо формулу замкненого типу. Інакше маємо квадратурну формулу відкритого типу.

Величина 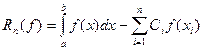називається похибкою квадратурної формули .

Якщо для деякої функції маємо 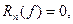то квадратурна формула являється для даної функції точною.

Квадратурна формула має алгебраїчний степінь точності 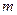, якщо вона є точною при і не точною при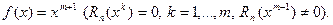

Звідси очевидно, що квадратурна формула степеня точності 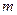є точною для всіх алгебраїчних многочленів степеня не вище за 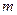, причому число 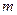- максимальний степінь таких многочленів.

Визначимо верхню оцінку точності для формули при фіксованому

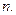
Лема. Степінь точності формули не може бути вище за при будь-якому виборі параметрів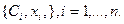

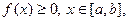ДоведенняРозглянемо довільну квадратурну формулу . Нехай Це многочлен степеня . Оскільки то 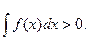З іншого боку, 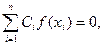тобто формула в даному випадку не є точною.

Формули чисельного обчислення однократного інтеграла називаються квадратурними формулами, подвійного й більшої кратності - кубатурними.

Наближеним значенням інтеграла будемо вважати вираз 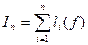, де 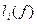– наближене значення інтеграла на частковому відрізку 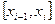. При цьому формула для обчислення 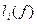називається найпростішою квадратурною формулою, а формула для обчислення 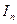– складеною квадратурною формулою.

7.1 Квадратурні формули Ньютона-Котеса

Розглянемо формули для наближеного обчислення інтегралів

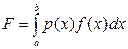. (7.1)

Обмежимося випадком, коли . Цей метод заснований на заміні підінтегральної функції інтерполяційним многочленом Лагранжа з вузлами, що розбивають відрізок на рівні частини. Такі формули називаються формулами Ньютона-Котеса.

Отже, нехай задана рівномірна сітка , , 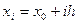. Тобто крок – величина постійна й розбиває відрізок на рівних інтервалів. Формули Ньютона-Котеса - формули замкненого типу. Позначимо 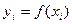. За наближену функцію оберемо інтерполяційний поліном Лагранжа

де .

Отже, заданий інтеграл може бути поданий у вигляді

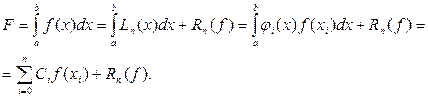
Таку квадратурну формулу називають квадратурною формулою інтерполяційного типу.

Нехай – виражена в сіткових кроках довжина 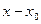. Тоді

;

.

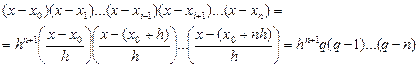
У такому випадку ваги можна розрахувати так:

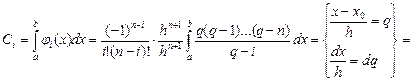
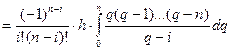. (7.2)

Формула (7.2) остаточно визначає ваги квадратурної формули Ньютона-Котеса. Замінимо в ній і введемо позначення 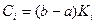. Тоді коефіцієнти

(7.3)

називаються коефіцієнтами Котеса. А сама квадратурна формула Ньютона-Котеса набирає вигляду

. (7.4)

Для коефіцієнтів Котеса мають місце співвідношення:

1 .

2 .

З’ясуємо питання про степінь точності квадратурної формули .

Нехай алгебраїчний многочлен степеня не вищого за 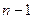. Тоді, згідно з властивостями інтерполяції , тобто 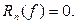Таким чином, інтерполяційна квадратурна формула має степінь точності не нижчий за .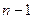

Звідси можна зробити висновок, що квадратурні коефіцієнти формули є єдиним розв’язком лінійної системи рівнянь

яка отримана із при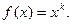

Розглянемо окремі випадки квадратурних формул Ньютона-Котеса з рівновіддаленими вузлами, в яких підінтегральна функція замінена на інтерполяційний поліном Лагранжа різного степеня.

 

7.1.1 Формула середніх (формула прямокутників)

 

Якщо на відрізку 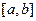взяти єдиний вузол квадратурної формули , то підінтегральна функція апроксимується поліномом нульового степеня – сталою 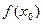. У зв’язку з тим, що симетричне розміщення вузлів у чисельному диференціюванні привело до підвищення точності, за вузол візьмемо середину відрізка інтегрування . Замінивши наближено площу криволінійної трапеції на площу прямокутника з висотою 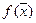та основою (b- a), одержимо формулу середніх

().

Це найпростіша квадратурна формула. Розклавши у ряд Тейлора довкола точки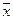

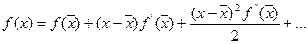
і підставивши цей ряд в інтеграл, одержимо значення похибки формули середніх

.

Формула середніх є точною для лінійної підінтегральної функції , оскільки тоді .

Природно, що точність формули для довільної можна підвищити, якщо скористатися докладнішою сіткою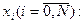

Це так звана складена формула середніх або формула прямокутників. У разі рівномірної сітки, тобто якщо , формула виглядатиме так:

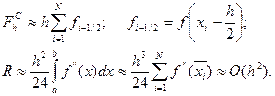
Наведені оцінки R справедливі, якщо існує неперервна 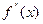; якщо ж 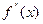кусково-неперервна, має місце лише мажорантна оцінка

.

7.1.2 Формула трапецій

Замінимо функцію на відрізку 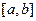інтерполяційним поліномом Лагранжа першого степеня з вузлами 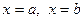, що відповідає заміні кривої на січну. Тоді значення шуканого інтеграла (площу криволінійної трапеції) можна наближено замінити на площу трапеції з висотою 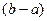та основами 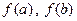. Отже, формула трапеції матиме вигляд

.

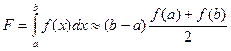Формула трапеції буде точною для лінійної підінтегральної функції з тієї самої причини, що й формула середніх.

На докладнішій сітці 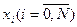одержимо складену формулу трапецій:

На рівномірній сітці вона стає такою:

).

Зазначимо, що для одержання залишкового члена формули трапеції потрібно замінити чисельний коефіцієнт (1/24) у залишковому члені формули середніх на (-1/24).

7.1.3 Формула Симпсона

Квадратурна формула Симпсона є частковим випадком квадратурних формул Ньютона-Котеса при 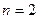. Тут підінтегральна функція заміняється інтерполяційним поліномом Лагранжа 2-го степеня (рисунок 7.2). Із цієї причини формулу Симпсона ще називають формулою парабол.

Розіб’ємо відрізок на 2 рівних відрізки і одержимо сітку 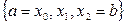, що містить три вузли. Формула Симпсона містить три коефіцієнти Котеса:

; .

.

; .

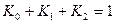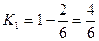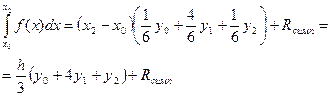(7.5)

Рис. – 7.2

Формула (7.5) є трьохточковою квадратурною формулою Симпсона.

Якщо розбити на парну кількість відрізків, що дорівнює 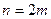, і до кожного часткового здвоєного проміжку 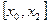,,…,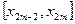застосувати формулу Симпсона, то одержимо складену формулу Симпсона

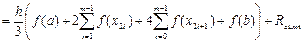. (7.6)

Урахувавши, що головні члени похибок у формулі середніх та формулі трапеції одного порядку, але різних знаків, можна одержати точнішу квадратурну формулу. Для цього скомбінуємо ці формули так, щоб головний член сумарної похибки цих квадратурних формул перетворився на нуль, тобто

.

Отже, дійдемо формули парабол

.

Формула парабол є точною для кубічної підінтегральної функції , оскільки в похибку 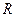входитиме , а вона для такої підінтегральної функції дорівнює нулю.

Ця формула має такий залишковий член:

тобто формула парабол має 4-й порядок похибки, а чисельний коефіцієнт досить малий. Через ці обставини формула парабол дає добру точність за відносно невеликого числа вузлів, якщо не дуже велика.

Прикладреалізації алгоритму чисельного інтегрування функції одного аргумента за формулою Симпсона на псевдокоді

f(x):

//Повертає значення підінтегральної функції