рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Образование
- /
- Методи Адамса
Реферат Курсовая Конспект
Методи Адамса
Методи Адамса - раздел Образование, Абсолютна і відносна похибки На Відміну Від Однокрокових Методів, У Яких Числовий Розв’Язо...
На відміну від однокрокових методів, у яких числовий розв’язок одержують тільки з диференціального рівняння і початкової умови, алгоритми Адамса складаються з двох частин: перша з них – стартова процедура для визначення  (наближені значення точного розв’язку в точках
(наближені значення точного розв’язку в точках 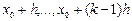 ), а друга – багатокрокова формула для одержання наближеного значення точного розв’язку
), а друга – багатокрокова формула для одержання наближеного значення точного розв’язку  . Потім ця формула застосовується рекурсивно для того, щоб за числовим розв’язком на
. Потім ця формула застосовується рекурсивно для того, щоб за числовим розв’язком на  послідовних кроках обчислити
послідовних кроках обчислити  і т.д.
і т.д.
Стартові значення можна одержати декількома способами. Дж. К. Адамс обчислював їх за допомогою розкладання точного розв’язку в ряд Тейлора. Інший спосіб полягає у використанні якого-небудь однокрокового методу, наприклад, Рунге-Кутта. Стартові значення часто також обчислюють методами Адамса низького порядку з дуже малим кроком.
Розглянемо чисельні методи розв’язання задачі Коші (8.1)-(8.2), які можуть бути задані формулою
 . (8.25)
. (8.25)
Тут значення розв’язку 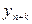 в точці
в точці  визначається через значення розв’язку в
визначається через значення розв’язку в  точках, що передують
точках, що передують  . Такий метод називається
. Такий метод називається  - кроковим.
- кроковим.
З класу (8.25) виділимо багатокрокові методи вигляду
 , (8.26)
, (8.26)
застосовувані на сітці з постійним кроком
 (8.27)
(8.27)
Різниця між найбільшим і найменшим значеннями індексу невідомої функції уn, що входить у рівняння (8.26), дорівнює  . Тому співвідношення (8.26) є різницевим рівнянням
. Тому співвідношення (8.26) є різницевим рівнянням  -го порядку, загальний розв’язок якого залежить від
-го порядку, загальний розв’язок якого залежить від  параметрів. Щоб виділити єдиний розв’язок цього рівняння, необхідно задати
параметрів. Щоб виділити єдиний розв’язок цього рівняння, необхідно задати  додаткових умов на функцію уп. Цими додатковими умовами є значення функції уn при n = 0,1,... ,
додаткових умов на функцію уп. Цими додатковими умовами є значення функції уn при n = 0,1,... ,  -1:
-1:
 (8.28)
(8.28)
які передбачаються відомими.
Використовуючи значення (8.28), з рівняння (8.26) при n=0 можна знайти  , потім, використовуючи значення
, потім, використовуючи значення  і покладаючи в (8.26) n =1, знайти
і покладаючи в (8.26) n =1, знайти  і т.д. Таким чином, даний метод чисельного розв’язання диференціального рівняння полягає в розв’язанні різницевої задачі Коші для різницевого рівняння (8.26) і початкових умов (8.28).
і т.д. Таким чином, даний метод чисельного розв’язання диференціального рівняння полягає в розв’язанні різницевої задачі Коші для різницевого рівняння (8.26) і початкових умов (8.28).
Якщо шуканий розв’язок 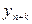 входить до правої частини цього рівняння, що буває, коли
входить до правої частини цього рівняння, що буває, коли 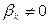 , то формула (8.26) визначає неявний метод. Якщо
, то формула (8.26) визначає неявний метод. Якщо  , то шуканий розв’язок до правої частини не входить і рівняння (8.26) може бути розв’язане відносно
, то шуканий розв’язок до правої частини не входить і рівняння (8.26) може бути розв’язане відносно 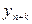 . У цьому випадку формула (8.26) визначає явний метод.
. У цьому випадку формула (8.26) визначає явний метод.
Виведемо групу явних багатокрокових формул. Для точок сітки введемо позначення 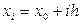 і припустимо, що нам відомі числові наближені значення
і припустимо, що нам відомі числові наближені значення 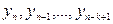 точного розв’язку
точного розв’язку 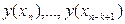 задачі (8.1)-(8.2).
задачі (8.1)-(8.2).
З диференціального рівняння випливає
 . (8.29)
. (8.29)
До правої частини (8.29) входить шуканий розв’язок 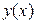 . Але оскільки нам відомі його наближені значення
. Але оскільки нам відомі його наближені значення 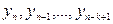 , то ми маємо також і величини
, то ми маємо також і величини
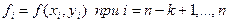 , (8.30)
, (8.30)
а тому природно замінити функцію 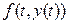 в (8.29) інтерполяційним многочленом, що проходить через точки
в (8.29) інтерполяційним многочленом, що проходить через точки 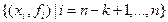 . Його можна виразити через скінченні різниці вигляду
. Його можна виразити через скінченні різниці вигляду  у такий спосіб:
у такий спосіб:
 (8.31)
(8.31)
(інтерполяційна формула Ньютона). Тоді чисельний аналог (8.29) задається формулою  , або після підстановки (8.31)
, або після підстановки (8.31)
 , (8.32)
, (8.32)
де коефіцієнти 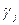 задовольняють рівність
задовольняють рівність
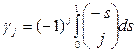 . (8.33)
. (8.33)
Числові значення цих коефіцієнтів наведені в таблиці 8.1.
Окремі випадки формули (8.32).
Для  , виразивши різниці назад через
, виразивши різниці назад через  , одержимо такі формули:
, одержимо такі формули:
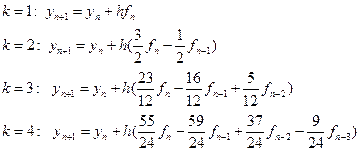
Зауваження. Для  ми маємо явний метод Ейлера.
ми маємо явний метод Ейлера.
Таблиця 8.1

| 0 1 2 3 4 5 6 7 8 |
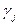
| 1 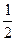       
|
Похибка апроксимації явного двокрокового методу Адамса має другий порядок.
Неявний двокроковий метод Адамса виглядає так:
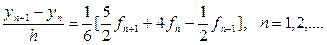
Похибка апроксимації має третій порядок .
8.2.3 Стійкість різницевих методів
Уведемо поняття стійкості різницевого методу. Для цього розглянемо різницеве рівняння багатокрокового методу
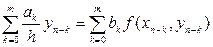 ,
,  . (8.34)
. (8.34)
Однорідне різницеве рівняння, що відповідає (8.34), має вигляд
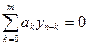 . (8.35)
. (8.35)
Вважають, що рівняння (8.35) є стійким за початковими даними, якщо існує постійна  , що не залежить від
, що не залежить від  , така, що при будь-яких початкових даних
, така, що при будь-яких початкових даних  здійснюється нерівність
здійснюється нерівність
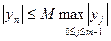 ,
,  .
.
Питання стійкості за початковими даними вирішується шляхом розгляду коренів так званого характеристичного рівняння, одержуваного з (8.35), якщо розв’язок цього рівняння шукати у вигляді 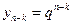 . Підставляючи таке
. Підставляючи таке  в (8.35) і скорочуючи на
в (8.35) і скорочуючи на 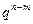 , одержимо характеристичне рівняння для визначення
, одержимо характеристичне рівняння для визначення 
 . (8.36)
. (8.36)
Теорема 1 Для стійкості рівняння (8.35) за початковими даними необхідно і достатньо, щоб виконувалася так звана умова коренів: усі корені  характеристичного рівняння знаходилися всередині або на границі одиничного кола комплексної площини, причому на границі не повинно бути кратних коренів.
характеристичного рівняння знаходилися всередині або на границі одиничного кола комплексної площини, причому на границі не повинно бути кратних коренів.
Теорема 2 Нехай 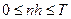 , умова коренів виконана,
, умова коренів виконана, 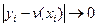 при
при 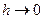 ,
, 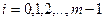 , і різницеве рівняння (8.34) апроксимує вихідне диференціальне рівняння (8.1). Тоді розв’язок різницевої задачі (8.34) збігається при
, і різницеве рівняння (8.34) апроксимує вихідне диференціальне рівняння (8.1). Тоді розв’язок різницевої задачі (8.34) збігається при 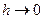 до розв’язку вихідної задачі (8.1).
до розв’язку вихідної задачі (8.1).
Інакше кажучи, з апроксимації і стійкості за початковими даними випливає збіжність на обмеженому відрізку 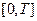 .
.
Сформульована умова стійкості, що базується на аналізі розміщення коренів характеристичного рівняння (8.36), є досить загальною. Конкретизуємо питання про стійкість різницевого рівняння стосовно до асимптотично стійких розв’язків рівняння (8.1). Нехай 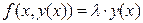 ,
,  , тобто
, тобто
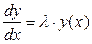 . (8.37)
. (8.37)
Розв’язок цього рівняння асимптотично стійкий, тобто для будь-яких  справедлива оцінка
справедлива оцінка
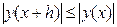 . (8.38)
. (8.38)
Логічно вимагати, щоб і різницеве рівняння давало розв’язок, що задовольняє властивість (8.38). Використовуючи явний метод Ейлера першого порядку апроксимації, одержимо різницевий аналог (8.37)
 ,
, 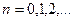 , (8.39)
, (8.39)
або  , тобто
, тобто  .
.
Оцінка (8.38) буде виконана для (8.39) лише за умови  , оскільки тоді
, оскільки тоді  . З
. З  випливає обмеження на крок
випливає обмеження на крок 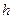 :
: 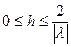 .
.
Різницевий метод (8.34) називається абсолютно стійким, якщо стійкість має місце при будь-яких 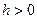 , й умовно стійким, якщо вона може бути забезпечена тільки введенням обмежень на крок
, й умовно стійким, якщо вона може бути забезпечена тільки введенням обмежень на крок 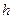 .
.
Як приклад абсолютно стійкого методу традиційно розглядається неявний метод Ейлера, що має перший порядок апроксимації
 . (8.40)
. (8.40)
З (8.40) випливає  , тобто
, тобто  завжди, при будь-яких
завжди, при будь-яких 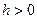 .
.
Умовна стійкість приводить до необхідності вибирати малі значення кроку 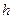 , що є недоліком явного методу. Неявний метод, позбавлений даного обмеження, має інший досить істотний недолік, обумовлений необхідністю розв’язувати на кожному кроці алгебраїчне рівняння (або систему рівнянь, у загальному випадку нелінійних).
, що є недоліком явного методу. Неявний метод, позбавлений даного обмеження, має інший досить істотний недолік, обумовлений необхідністю розв’язувати на кожному кроці алгебраїчне рівняння (або систему рівнянь, у загальному випадку нелінійних).
Запишемо різницеві рівняння (8.34) для задачі (8.37)
 ,
,  ,(8.41)
,(8.41)
де  - у загальному випадку комплексний параметр.
- у загальному випадку комплексний параметр.
Характеристичне рівняння для (8.41) має вигляд
 . (8.42)
. (8.42)
При малих 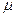 корені (8.42) близькі до коренів (8.35).
корені (8.42) близькі до коренів (8.35).
Областю стійкості методу (8.34) називається множина точок комплексної площини  , для яких метод, що застосований до рівняння спеціального вигляду (8.37), є стійким.
, для яких метод, що застосований до рівняння спеціального вигляду (8.37), є стійким.
Для явного методу Ейлера умова стійкості 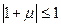 при комплексному
при комплексному 
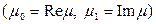 виглядає в такий спосіб:
виглядає в такий спосіб:  , тобто областю стійкості є коло одиничного радіуса, центр якого знаходиться в точці
, тобто областю стійкості є коло одиничного радіуса, центр якого знаходиться в точці 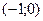 комплексної площини.
комплексної площини.
Для неявного методу Ейлера умова 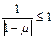 відповідає нерівності
відповідає нерівності  , тобто областю стійкості є зовнішність кола одиничного радіуса з центром у точці
, тобто областю стійкості є зовнішність кола одиничного радіуса з центром у точці  .
.
Різницевий метод називається  стійким, якщо область його стійкості включає ліву півплощину
стійким, якщо область його стійкості включає ліву півплощину  (або
(або 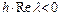 ). Варто звернути увагу на те, що рівняння (8.37) асимптотично стійке при
). Варто звернути увагу на те, що рівняння (8.37) асимптотично стійке при 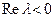 . Отже,
. Отже,  стійкий різницевий метод є абсолютно стійким (тобто стійким при будь-яких
стійкий різницевий метод є абсолютно стійким (тобто стійким при будь-яких 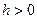 ), якщо стійким є розв’язок вихідного диференціального рівняння.
), якщо стійким є розв’язок вихідного диференціального рівняння.
З вищезазначеного видно, що неявний метод Ейлера має властивість  стійкості, а явний метод – не має.
стійкості, а явний метод – не має.
Розглянемо ще один неявний метод більш високого порядку апроксимації (другого):
 . (8.43)
. (8.43)
Цей метод виходить заміною інтеграла від правої частини (8.1) за формулою трапецій. Стосовно рівняння (8.37) метод (8.43) виглядає так:  , тобто
, тобто 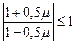 , якщо
, якщо  . Отже, метод (8.43) належить до
. Отже, метод (8.43) належить до стійких методів.
стійких методів.
Доведеними є такі положення:
-серед методів (8.43) не існує явних  стійких методів;
стійких методів;
-серед неявних лінійних багатокрокових методів немає стійких методів, що мають порядок точності вище другого.
стійких методів, що мають порядок точності вище другого.
 стійкі різницеві схеми досить ефективні при розв’язанні так званих жорстких систем рівнянь, оскільки ці методи не накладають обмежень на крок
стійкі різницеві схеми досить ефективні при розв’язанні так званих жорстких систем рівнянь, оскільки ці методи не накладають обмежень на крок 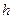 . Розглянемо докладніше це твердження.
. Розглянемо докладніше це твердження.
8.2.4 Жорсткі диференціальні рівняння
Система звичайних диференціальних рівнянь
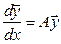 (8.44)
(8.44)
з незалежною від 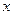 матрицею
матрицею 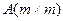 називається жорсткою, якщо
називається жорсткою, якщо  ,
, 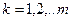 і відношення
і відношення 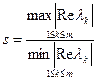 велике, де
велике, де  - власні числа матриці
- власні числа матриці 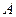 . Величина
. Величина  називається числом жорсткості. Якщо матриця
називається числом жорсткості. Якщо матриця 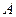 залежить від
залежить від 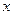 , то і
, то і  - залежать від
- залежать від 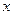 , тоді вводиться змінне число жорсткості
, тоді вводиться змінне число жорсткості

і оперують з величиною 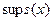 на відрізку інтегрування.
на відрізку інтегрування.
Відмінною рисою жорстких систем є наявність у їхньому розв’язку як швидко, так і повільно спадних компонентів. При  розв’язок системи практично визначається повільно спадним компонентом, однак, якщо скористатися явними різницевими методами, то швидко спадна складова буде негативно впливати на стійкість, і в результаті весь розрахунок необхідно вести з малим кроком інтегрування. При використанні ж неявних методів обмеження на крок зняті, і його величину визначають з умови досягнення потрібної точності, не хвилюючись особливо за стійкість.
розв’язок системи практично визначається повільно спадним компонентом, однак, якщо скористатися явними різницевими методами, то швидко спадна складова буде негативно впливати на стійкість, і в результаті весь розрахунок необхідно вести з малим кроком інтегрування. При використанні ж неявних методів обмеження на крок зняті, і його величину визначають з умови досягнення потрібної точності, не хвилюючись особливо за стійкість.
При розв’язанні жорстких систем диференціальних рівнянь добре зарекомендував себе метод Гіра, що належать до чисто неявних багатокрокових різницевих методів, загальна формула яких виглядає так:  ,
,
тобто розглядається частковий варіант методу (8.43), коли  , а
, а  .
.
При  і
і  маємо
маємо  , тобто неявний метод Ейлера. При
, тобто неявний метод Ейлера. При 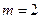 і
і  методи виглядають так:
методи виглядають так:
 , (8.45)
, (8.45)
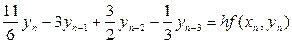 . (8.46)
. (8.46)
Різницеве рівняння (8.45) має другий порядок точності, а (8.46) - третій. Щоб знайти область стійкості методу, варто записати аналогічні рівняння для диференціального рівняння (8.46). Наприклад, (8.45) набере вигляду
 .
.
Відповідне характеристичне рівняння запишеться в такий спосіб:
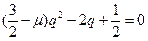 . (8.47)
. (8.47)
Потрібно визначити область комплексної площини  , у точках якої обидва корені (8.47) за модулем менше одиниці. Виявляється, що ця область цілком розміщується у правій півплощині і метод (8.45) є
, у точках якої обидва корені (8.47) за модулем менше одиниці. Виявляється, що ця область цілком розміщується у правій півплощині і метод (8.45) є  стійким.
стійким.
8.3 Метод скінченних різниць
Основний зміст методу можна легко пояснити на прикладі розв'язання задач в одновимірній області.
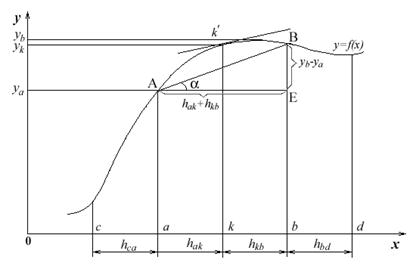
Рис. – 8.3
Виразимо похідну функції 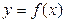 лінійною комбінацією значень цієї функції у визначених точках розглянутого проміжку зміни незалежних змінних, які називаємо вузлами. Існує кілька способів вираження похідної подібним чином. Наприклад, першу похідну функції
лінійною комбінацією значень цієї функції у визначених точках розглянутого проміжку зміни незалежних змінних, які називаємо вузлами. Існує кілька способів вираження похідної подібним чином. Наприклад, першу похідну функції  у вузлі
у вузлі 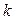 (рис. 8.3) можна виразити такими скінченними різницями (дивись розділ 6):
(рис. 8.3) можна виразити такими скінченними різницями (дивись розділ 6):

| (8.48) (8.49) (8.50) |
Відстань (крок) між вузлами беруть однаковою  і формула (8.50) записується у вигляді
і формула (8.50) записується у вигляді

| (8.51) |
Другу похідну можна наближено виразити (мал. 8.3), застосовуючи формулу (8.51) при  в такий спосіб:
в такий спосіб:

| (8.52) |
Застосовується також формула для другої похідної, отримана на основі виразів (8.48), (8.49) для однобічних різниць (при  ):
):

| (8.53) |
Розв'язання крайової задачі методом скінченних різниць зводиться до обчислення значень шуканої функції в обраних вузлах шляхом розв'язання відповідної системи лінійних алгебраїчних рівнянь.
Докладно розглянемо різницевий метод на прикладі крайової задачі для лінійного рівняння другого порядку з крайовими умовами першого роду
 , (8.54)
, (8.54)
 ,
,  . (8.55)
. (8.55)
Уведемо на [a,b] сітку  , що для спрощення викладень будемо вважати рівномірною. Наближено виразимо другу похідну від розв’язку через значення розв’язку у вузлах сітки
, що для спрощення викладень будемо вважати рівномірною. Наближено виразимо другу похідну від розв’язку через значення розв’язку у вузлах сітки  ; наприклад, скористаємося найпростішою апроксимацією
; наприклад, скористаємося найпростішою апроксимацією
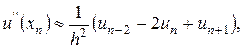
 .
.
Таку апроксимацію можна записати в будь-якому вузлі сітки  . Якщо підставити її в рівняння (8.54), то рівняння стане наближеним; точно задовольняти це рівняння буде вже не шуканий розв’язок
. Якщо підставити її в рівняння (8.54), то рівняння стане наближеним; точно задовольняти це рівняння буде вже не шуканий розв’язок  , а деякий наближений розв’язок
, а деякий наближений розв’язок  . Виконуючи цю підстановку і позначаючи
. Виконуючи цю підстановку і позначаючи  і
і  , одержимо
, одержимо
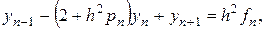
 . (8.56)
. (8.56)
Ця формула складається з N-1 алгебраїчного рівняння, а невідомими в ній є наближені значення розв’язку у вузлах сітки. Число невідомих  дорівнює N+1, тобто воно більше, ніж число рівнянь (8.56). Відсутні два рівняння легко одержати з крайових умов (8.55):
дорівнює N+1, тобто воно більше, ніж число рівнянь (8.56). Відсутні два рівняння легко одержати з крайових умов (8.55):
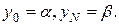 (8.57)
(8.57)
У випадку використання граничних умов другого роду апроксимація проводиться за допомогою формул чисельного диференціювання першого порядку:
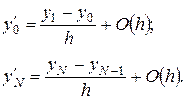
Розв’язуючи алгебраїчну систему (8.56), (8.57), знайдемо наближений розв’язок.
Як ілюстрацію проведемо повне дослідження розглянутого вище прикладу, додатково вимагаючи  .
.
Спочатку розглянемо питання про існування різницевого розв’язку. Вихідна задача (8.54) була лінійною, різницева апроксимація (8.56)– теж лінійна. Завдяки цьому система (8.56,8.57) виявилася системою лінійних алгебраїчних рівнянь. Оскільки 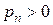 , то в матриці цієї системи діагональні елементи переважають: у кожному рядку модуль діагонального елемента більше суми модулів інших елементів, при цьому розв’язок лінійної системи існує і єдиний.
, то в матриці цієї системи діагональні елементи переважають: у кожному рядку модуль діагонального елемента більше суми модулів інших елементів, при цьому розв’язок лінійної системи існує і єдиний.
Обчислити розв’язок лінійної системи рівнянь завжди можна методом виключення Гауса. У даному випадку завдяки використанню триточкової апроксимації (8.54) система (8.56) має тридіагональну матрицю. Тому розв’язок доцільніше знаходити за допомогою різновиду методу Гауса – методом прогонки.
Щоб оцінити похибку наближеного розв’язку задачі, використовують інформацію, отриману в процесі чисельних розрахунків (такі оцінки називаються апостеріорними). Найефективнішими можна вважати оцінки з подвійним перерахунком.
Наявність наближених значень 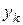 і
і 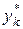 , обчислених відповідно з кроками h і h/2, дає можливість зробити оцінку. Похибка методу – це
, обчислених відповідно з кроками h і h/2, дає можливість зробити оцінку. Похибка методу – це 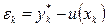 , визначена в точці
, визначена в точці  .
.
Отже, якщо 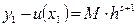 , де М – невідомий коефіцієнт пропорційності, s – порядок точності методу, то
, де М – невідомий коефіцієнт пропорційності, s – порядок точності методу, то
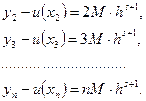
Виходить, для похибки в точці  при визначенні розв’язку з кроком h маємо рівність
при визначенні розв’язку з кроком h маємо рівність  , а при розв’язку з кроком h/2 – рівність
, а при розв’язку з кроком h/2 – рівність
 . (8.58)
. (8.58)
Знайшовши різницю між наведеними вище рівностями і розв’язавши отриману рівність відносно невідомого коефіцієнта М, визначимо
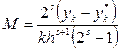 .
.
Підставивши це значення М у формулу (8.58), одержимо 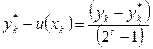 . Звідси для абсолютної похибки в точці
. Звідси для абсолютної похибки в точці  остаточно одержимо таку рівність:
остаточно одержимо таку рівність:
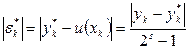 .
.
Таку оцінку абсолютної похибки методу називають, як відомо, правилом Рунге.
Зупинимося на стійкості розрахунку. Якщо  , то задача Коші для рівняння (8.54) погано обумовлена, причому, чим більше p(x), тим гірша її стійкість. А з оцінки (8.58) видно, що похибка нашого різницевого розв’язку при великих p(x) мала. Звідси виходить, що добре побудовані різницеві схеми не чуттєві до нестійкості задачі Коші. У випадку, коли
, то задача Коші для рівняння (8.54) погано обумовлена, причому, чим більше p(x), тим гірша її стійкість. А з оцінки (8.58) видно, що похибка нашого різницевого розв’язку при великих p(x) мала. Звідси виходить, що добре побудовані різницеві схеми не чуттєві до нестійкості задачі Коші. У випадку, коли  , не виконується достатня умова збіжності ітераційного процесу для систем лінійних алгебраїчних рівнянь, однак у практичних обчисленнях дана обставина, як правило, виявляється несуттєвою і не викликає складностей в одержанні розв’язку.
, не виконується достатня умова збіжності ітераційного процесу для систем лінійних алгебраїчних рівнянь, однак у практичних обчисленнях дана обставина, як правило, виявляється несуттєвою і не викликає складностей в одержанні розв’язку.
8.4 Різницева задача на власні значення
Розглянемо диференціальну задачу Штурма-Ліувілля

Числа  і відповідні функції u(x)
і відповідні функції u(x)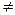 0, що задовольняють поставлену крайову задачу називаються власними числами і власними функціями відповідно. Для даної задачі
0, що задовольняють поставлену крайову задачу називаються власними числами і власними функціями відповідно. Для даної задачі

Зауважимо, що функції um(x) є лінійно незалежними і взаємно ортогональними й можуть бути нормовані.
Для різницевої задачі на власні значення
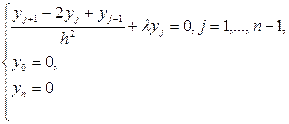
відповідні власні функції і власні значення різницевої задачі мають вигляд
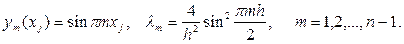
Відмітимо, що функції ym(x) є лінійно незалежними і взаємно ортогональними, як і в диференціальному випадку, й можуть бути нормовані.
Питання і завдання до розділу 8
1 Постановка задачі Коші. Дискретна задача Коші: основні поняття і визначення (сітка, сіткові функції, чисельний метод, апроксимація, збіжність).
2 Виведення формули методу Ейлера, його геометрична інтерпретація, стійкість, оцінка похибки, вплив обчислювальної похибки.
3 Методи Рунге-Кутта. Виведення формул. Оцінка похибки.
4 Явні однокрокові методи. Оцінка похибки за правилом Рунге.
5 Чисельне розв’язання задачі Коші для систем диференціальних рівнянь.
6 Апроксимація, стійкість і збіжність чисельних методів розв’язання задачі Коші.
7 Багатокрокові методи Адамса.
8 Виведення формул методу прогнозу і корекції.
9 Жорсткі задачі і методи їхнього розв’язання.
10 Застосовуючи метод Ейлера , знайти розв’язок задачі Коші 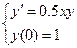 у трьох послідовних точках:
у трьох послідовних точках: 
11 Для задачі Коші  виконати один крок довжини 0.1 за методом Ейлера й оцінити похибку знайденого значення за правилом Рунге.
виконати один крок довжини 0.1 за методом Ейлера й оцінити похибку знайденого значення за правилом Рунге.
12 Методом Рунге-Кутта 2 порядку точності знайти розв’язок системи диференціальних рівнянь  у двох послідовних точках
у двох послідовних точках  ,
, .
.
13 Оцінити похибку апроксимації похідної різницевим відношенням  .
.
14 Звести рівняння другого порядку до системи рівнянь першого порядку і скласти розрахункові формули методу прогнозу і корекції для розв’язку отриманої системи рівнянь 
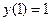 ,
, 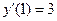 .
.
15 З'ясувати, чи апроксимують методи
a)  b)
b) 
перше рівняння задачі Коші

16 Для розв’язання задачі Коші  застосовується метод вигляду
застосовується метод вигляду 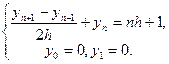 Визначити порядок апроксимації.
Визначити порядок апроксимації.
17 Дано систему ОДУ першого порядку з постійними коефіцієнтами , причому відомі власні значення матриці
, причому відомі власні значення матриці 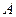 :
:
a) 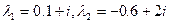 ,
,
b)  ,
,
c)  .
.
У яких випадках систему можна вважати жорсткою?
Список літератури
1. Ляшко И.И., Макаров В.Л., Скоробагатько А.А. Методы вычислений.–Киев: Вища школа, 1977,-406с.
2. Гаврилюк І.П., Макаров В.Л. Методи обчислень. — К.:Вища школа, 1995, ч.1, ч.2.
3. Бахвалов Н.С. Численные методы. – М.:Наука, 1973.–632с.
4. Данилович В., Кутнів М. Чисельні методи. — Львів:Кальварія, 1998.
5. Форсайт Дж., Молер К. Численное решение систем линейных алгебраических уравнений.– М.: Мир, 1969.–168с.
6. Калиткин Н.Н. Численные методы,– М.: Наука, 1978. – 512с.
7. Волков Е.А. Численные методы,– М.: Наука, 1982. – 256с.
8. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. – М.: Мир, 1980. –280с.
9. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 368с.
10. Крылов В.И., Бобков В.В., Монастырный П.Н. Вычислительные методы высшей математики: В 2-х т. – Минск: Вышэйшая школа, 1972.- Т. 1. – 304с.; Т.2.-400с.
11. Березин И.С., Жидков Н.П. Методы вычислений: В 2–х т. – М., 1959. Т.1.– 464 с.;Т.2 – 602 с.
12. Марчук Г.И. Методы вычислительной математики. - М.: Наука, 1989. - 608 с.
13. Боглаев Ю.П. Вычислительная математика и программирование.- М.: Высш.школа,1990.-544с.
14. Григоренко Я.М., Панкратова Н.Д. Обчислювальні методи в задачах прикладної математики.-К.: Либідь,1995.-277с.
15. Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране.-М.:Мир,1977.-580с.
16. Самарский А.А. Теория разностных схем. — М.:Наука, 1989.
17. Самарский А.А., Гулин А.В. Численные методы. — М.:Наука, 1989.
18. Самарский А.А. Введение в численные методы. - М.: Наука, 1987. - 288 с.
– Конец работы –
Эта тема принадлежит разделу:
Абсолютна і відносна похибки
С... Розділ Основні проблеми чисельного розв язання Класифікація похибок...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Методи Адамса
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов