Схеми Рунге-Кутта четвертого порядку

Методом Рунге-Кутта можна будувати схеми різного порядку точності.

Так схема ламаних Ейлера (8.5) є схемою Рунне-Kyттa першого порядку точності. Найбільш уживані схеми четвертого порядку точності. Наведемо без виведення найчастіше використовувані з них:

,

,

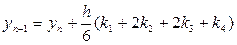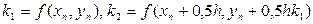(8.15)

Відзначимо, що формули більш високого порядку точності практично не вживаються через громіздкість, що зростає значно швидше, ніж точність формули.

Схеми Рунге-Кутта мають ряд переваг:

1) мають досить високий ступінь точності (за винятком схеми ламаних);

2) є явними, тобто значення обчислюється за раніше знайденими значеннями;

3) допускають використання змінного кроку, що дає можливість зменшити його там, де функція швидко змінюється, і збільшити в іншому випадку;

4) є легко застосовними, тому що для початку розрахунку досить вибрати сітку 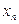і задати значення .

Зазначені властивості схем досить корисні при розрахунках на ЕОМ.

Оцінки похибок різних схем Рунге-Кутта пов'язані з максимумами модулів відповідних похідних функції 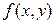досить складними формулами типу (8.8). У зв'язку з цим при розв’язанні конкретної задачі виникає питання, якою з формул Рунге-Кутта доцільно користуватися і як обирати крок сітки.

Якщо f(х,у) неперервна й обмежена разом зі своїми четвертими похідними, то гарні результати дає схема четвертого порядку (8.15). Якщо права частина рівняння (8.1) не має зазначених похідних, то граничний порядок точності схеми (8.15) не може бути реалізований. Тоді доцільно користуватися схемами меншого порядку точності, що дорівнює порядкові наявних похідних, наприклад для двічі неперервно диференційованої функції f(x,y) —схемами (8.12) і (8.1З).

Крок сітки варто вибирати настільки малим, щоб забезпечити необхідну точність розрахунку. З огляду на складність виразів залишкових членів (типу 8.8) апріорною (від лат. a priori — з попередніх) оцінкою точності для вибору кроку при практичних розрахунках не користуються, а заміняють її, наприклад, розрахунками зі згущенням сітки і дають апостеріорну (від лат. a posteriori - з наступного) оцінку точності.

Зауваження. Якщо функція f(x,y) досить гладка, але швидко змінюється на , схеми Рунге-Кутта як низького, так і високого порядку точності вимагають неприйнятно малого кроку для отримання задовільного результату. Для таких задач використовуються спеціальні методи, орієнтовані на даний вузький клас задач.

Одним із найбільш простих, широко застосовуваних і досить ефективних методів оцінки похибки й уточнення отриманих результатів у наближених обчисленнях з використанням сіток є правило Рунге.

Нехай маємо наближену формулу 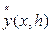для обчислення величини у(х) за значеннями на рівномірній сітці 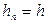і залишковий член цієї формули має такий вигляд:

. (8.16)

Виконаємо тепер розрахунок за тією самою наближеною формулою для тієї самої точки х, але використовуючи рівномірну сітку з іншим кроком rh, r < 1. Тоді отримане значення 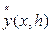пов'язане з точним значенням співвідношенням

. (8.17)

Зауважимо, що .

Маючи два розрахунки на різних сітках, неважко оцінити величину похибки. Для цього віднімемо (8.17) з (8.16) і одержимо першу формулу Рунге

(8.18)

Перший з доданків є головним членом похибки. Таким чином, розрахунок за другою сіткою дозволяють оцінити похибку розрахунку за першою (з точністю до членів більш високого порядку).

Відзначимо, що при користуванні правилом Рунге практично досить застосувати формулу оцінки похибки у вигляді

, (8.19)

де - наближені значення розв’язку рівняння в одній і тій самій точці, отримані з кроком h і h/2. При цьому необхідна точність може вважатися досягнутою, якщо величина R не перевищує заданої похибки у всіх збіжних вузлах.

Застосування правила Рунге дає можливість одержувати результати досить високої точності, використовуючи обчислення за формулами низького порядку точності, тобто дозволяє уточнити результати.

Відзначимо, що правило Рунге застосовується й у випадках, якщо сітки з різним числом вузлів нерівномірні, але їх можна описати функціями h(x), відношення яких . Величина відношення кроків r у правилі Рунге може бути будь-якою, але використовується вона найчастіше для цілого r, при цьому всі вузли менш докладної сітки повинні бути вузлами більш докладної. Особливо зручно згущати сітки вдвічі. У цьому випадку у вузлах, що є загальними для декількох сіток, можна уточнювати y(x) безпосередньо за правилом Рунге (8.18). Якщо розв’язок не уточнюється, а лише оцінюється його похибка, то використовується формула (8.19). Можна уточнити значення у(х,h) у всіх вузлах найдетальнішої сітки.

Використовуємо збіжніі вузли сіток для визначення виправлень до значень фікції :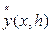

.

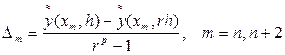Значення виправлень в інших вузлах знайдемо інтерполяцією. Для рівномірних сіток покладемо . Потім обчислимо уточнені значення 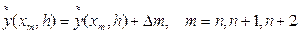. Цей спосіб узагальнюється на будь-яке число сіток.

Відзначимо ще раз, що виконати уточнення, як правило, простіше, ніж скласти і використовувати схему високого порядку точності.

Похибки наведених схем Рунге-Кутта визначаються максимальними значеннями відповідних похідних.

Оцінку похибки легко одержати для окремого випадку правої частини диференціального рівняння .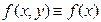

У цьому випадку розв’язок рівняння може бути зведений до квадратури й усі схеми різницевого розв’язку переходять у формули чисельного інтегрування. Наприклад, схема (8.14) набирає вигляду

,

тобто має вигляд формули трапецій, а схема (8.15) переходить у схему

,

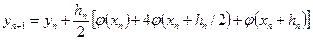що являє собою формулу Симпсона з кроком .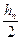

Мажорантні оцінки похибок формул трапецій і Симпсона відомі. З них видно, що точність схем Рунге-Кутта досить висока.

Приклад. Знайти наближений розв’язок задачі Коші для звичайного диференціального рівняння (ОДУ) 1 порядку

у'(t)=2ty, t0=0, T=1, y(0) =1 та оцінити його похибку.

Вихідні дані:

Права частина: 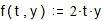. Початкове значення: .

Кінці відрізка: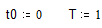.Крок сітки: .

Число вузлів сітки: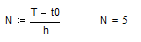.Функція, що реалізує явний метод Ейлера, повертає вектор розв’язку:

 

 

Вхідні параметри:

f - функція правої частини;

y0 - початкове значення;

t0 - початкова точка відрізка;

h - крок сітки;

N - число вузлів сітки.

Обчислення розв’язку за методом Ейлера:

Обчислення розв’язку за методом Рунге-Кутта 4 порядку точності:

;

вхідні параметри:

y - вектор початкових значень;

t0- початкова точка відрізка;

T - кінцева точка відрізка;

N - число вузлів сітки;

f - функція правої частини. Функція rkfixed повертає матрицю, перший стовпець якої містить вузли сітки, а другий - наближений розв’язок у цих вузлах.

Точний розв’язок: .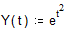

Точний розв’язок у вузлах сітки:

 

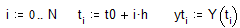
Розв’язок за методом Розв’язок за методом Точний розв’язок

Ейлера Рунге-Кутта

Графіки наближених і точних розв’язків

Обчислення похибки за правилом Рунге:

Обчислення наближених розв’язків із кроком h/2:

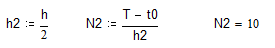
Обчислення похибок:

.

Приклад реалізації алгоритму методу Рунге-Кутта четвертого порядку з заданою точністю 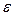на псевдокоді.

f(x,y):

//повертає значення заданої похідної при заданих x та y

end

//BeginValue – початкові умови

//YF – відповідь – масив значень функції

//h – крок

//n – кількість точок розбиття

//eps – точність розрахунку

//Метод Рунге-Кутта 4-го порядку

SolveRungeKutt(BeginValue,YF,h,n,eps):