Кубатурна формула типу Симпсона

Нехай областю інтегрування є K-вимірний просторовий паралелепіпед 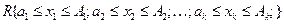(рис.7.6), сторони якого паралельні осям координат. Кожний із проміжків розіб'ємо навпіл точками:

, де .

Усього, таким чином, одержимо 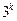точок сітки. Маємо

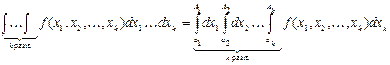. (7.23)

Знаходимо K-вимірний інтеграл, обчислюючи кожний внутрішній інтеграл за квадратурною формулою Симпсона на відповідному відрізку. Проведемо повністю всі обчислення для випадку K=2:

Застосовуючи до кожного інтеграла знову формулу Симпсона, одержимо:

,

або

(7.24)

Формулу (7.24) будемо називати кубатурною формулою Симпсона. Отже,

(7.25)

де – сума значень підінтегральної функції у вершинах прямокутника 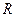, 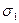– сума значень 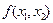у серединах сторін прямокутника 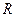, 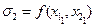– значення функції 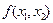в центрі прямокутника . Кратності цих значень позначені на рис. 7.6.

Якщо розміри просторового паралелепіпеда 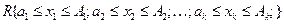великі, то для збільшення точності кубатурної формули область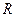

розбивають на систему паралелепіпедів, до кожного з яких застосовують кубатурну формулу Симпсона.

Знову розглянемо випадок K=2. Покладемо, що сторони прямокутника 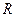ми розділили відповідно на й однакових частин; у результаті вийшла відносно велика мережа 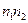прямокутників (на рис. 7.7 вершини цих прямокутників відзначені більшими кружками). Кожний із цих прямокутників, у свою чергу, розділимо на чотири однакові частини. Вершини цієї останньої дрібної мережі прямокутників візьмемо за вузли 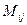кубатурної формули.

Нехай і 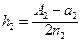. Тоді мережа вузлів буде мати координати: ;

Для скорочення введемо позначення

Застосовуючи формулу (7.24) до кожного із прямокутників великої мережі, будемо мати (рис.7.7):

Звідси, виконавши зведення подібних членів, остаточно знаходимо:

(7.26)

 

 

 

де коефіцієнти є відповідними елементами матриці

Якщо область інтегрування – довільна, то будуємо паралелепіпед , сторони якого паралельні осям координат (рис. 7.8). Розглянемо допоміжну функцію

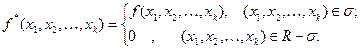
У такому випадку маємо

Останній інтеграл приблизно може бути обчислений за загальною кубатурною формулою (7.26).

Питання і завдання до розділу 7

1 Найпростіші квадратурні формули ( прямокутників, трапецій, Симпсона), геометрична ілюстрація, оцінки похибки. Точність квадратурних формул.

2 Квадратурні формули інтерполяційного типу: виведення формул, оцінки похибки.

3 Квадратурні формули Гауса: виведення формул, точність формул.

4 Правило Рунге практичної оцінки похибки. Адаптивні процедури чисельного інтегрування.

5 Обчислити наближено з кроком h=1 інтеграл 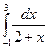за формулами прямокутників, трапецій, Симпсона. Оцінити похибку теоретично.

6 Переконатися в тім, що формула прямокутників є точною для многочленів , а формула Симпсона – для многочленів .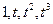

7 Оцінити теоретично значення кроку інтегрування h для наближеного обчислення інтеграла 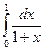за формулою трапецій з точністю .

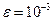8 Оцінити теоретично значення кроку інтегрування h для наближеного обчислення інтеграла 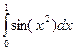по формулі Симпсона з точністю .

9 Одержати квадратурні формули прямокутників і трапецій із загальної формули інтерполяційного типу.

10 Переконатися, що квадратурна формула Гауса з одним вузлом точна для многочленів .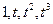

11 Обчислити інтеграл за формулами трапецій і Симпсона з точністю 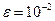, використовуючи правило Рунге оцінки похибки.

12 Знайти оцінку похибки обчислення інтеграла за складеною формулою

.

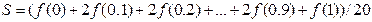13 Оцінити мінімальне число розбиттів відрізка N інтегрування для наближеного обчислення інтеграла 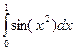за складеною формулою трапецій, що забезпечує точність .

14 Обчислити інтеграли , де , k=0,1,...,5 аналітично й використовуючи квадратурну формулу Симпсона із кроком h = (b-a)/2. Для многочленів якого степеня використовувана квадратурна формула точна й чому? Оцінити похибку інтегрування за правилом Рунге.

15Обчислити значення інтеграла аналітично й, використовуючи формулу прямокутників із кроками 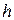: , ,…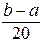...(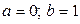). При зазначених значеннях 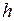знайти абсолютну похибку й оцінки теоретичної абсолютної похибки. На одному кресленні побудувати графіки знайдених похибок.

16Побудувати графік функції . Для обчислення інтеграла з точністю 10^-8 використати квадратурну формулу трапецій і правило Рунге оцінки похибки.

17Обчислити значення інтеграла із задачі 14, використовуючи квадратурну формулу Гауса з одним, двома, трьома, чотирма вузлами. Визначити абсолютну похибку результату. Побудувати гістограму залежності похибки від числа вузлів. Переконатися, що квадратурні формули Гауса з N+1 (N=0,1,2,3) вузлами точні для многочленів 1, t,…,t^m, де m=2N+1.

18Обчислити наближено площу фігури, обмеженої кривими 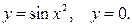Точки перетину кривих знайти графічно. Для обчислення інтегралів з точністю 10^-8 використати квадратурну формулу Симпсона і правило Рунге оцінки похибки.

19Наближено обчислити подвійний інтеграл по прямокутній області з точністю 0.001.

20 Функція y=y(x) задана таблицею своїх значень:

x		0.1	0.2	0.3	0.4
y		1.2	1.24	0.76	0.6

Обчислити наближене значення інтеграла 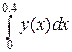за квадратурними формулами трапецій і Симпсона.

21Побудувати квадратурну формулу , точну для многочленів найбільш високого степеня, використовуючи метод невизначених коефіцієнтів.

22 Знайти наближене значення інтеграла із кроком , використовуючи квадратурні формули прямокутників, трапецій, Симпсона. Оцінити похибку формули чисельного інтегрування двома способами: використовуючи теоретичну оцінку похибки та правило Рунге.

23 З яким кроком інтегрування потрібно обчислювати наближене значення інтеграла 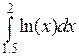за формулою трапецій для того, щоб забезпечити точність 0.00001.

Розділ 8

Чисельне розв’язання звичайних диференціальних рівнянь

 

Звичайними диференціальними рівняннями називаються рівняння, що пов’язують функцію та її похідні з однією незалежною змінною. Якщо незалежних змінних більше, ніж одна, то рівняння називається диференціальним рівнянням з частинними похідними.

За допомогою звичайних диференціальних рівнянь будуються моделі руху систем взаємодіючих часток, електротехнічних процесів у електричних ланцюгах, кінетики хімічних реакцій, процесів заселення рівнів енергії у високотемпературних середовищах і багатьох інших об'єктів і процесів.

До задач для звичайних диференціальних рівнянь зводяться деякі задачі для рівнянь у частинних похідних, коли рівняння дозволяє провести відокремлення змінних (наприклад, при обчисленні енергетичного спектра часток у полях визначеної симетрії).

Звичайне диференціальне рівняння будь-якого порядку за допомогою заміни змінних може бути зведене до системи рівнянь першого порядку.

У загальному вигляді перетворення є таким:

диференціальне рівняння -го порядку

заміною змінних зводяться до системи рівнянь першого порядку

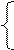
де позначено .

Відповідно до викладеного далі будуть розглядатися системи рівнянь першого порядку:

Розв’язок системи -го порядку залежить від параметрів Єдиний розв’язок визначається при використанні додаткових умов для шуканої функції. У залежності від того, яким чином ставляться такі умови, розрізняють три типи задач для звичайних диференціальних рівнянь: задача Коші, крайова задача і задача на власні значення.

У задачі Коші всі додаткові умови ставляться в одній точці . Розв’язок шукається на деякому інтервалі

Якщо праві частини 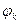рівнянь неперервні в деякому околі початкової точки 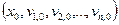і задовольняють умову Ліпшиця за змінними , то розв’язок задачі Коші існує, єдиний і неперервно залежить від координат початкової точки, тобто задача є коректною. Умова Ліпшиця формулюється в такий спосіб:

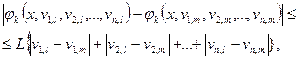
для будь-яких точок , де 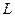- деяка константа.

Можна виділити три класи методів розв’язання звичайних диференціальних рівнянь: точні, наближені та чисельні.

Точні методи передбачають одержання розв’язку у вигляді комбінації елементарних функцій або у вигляді квадратур від останніх. Можливості точних методів обмежені.

Наближені методи зводяться до побудови послідовності функцій , що мають границею шукану функцію 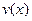. Обриваючи цю послідовність на якомусь 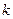, одержують наближений розв’язок.

Найбільш універсальними методами розв’язання є чисельні. Їхній основний недолік - можливість одержання тільки часткового розв’язку.

Варто зауважити, що успіх від застосування чисельного методу суттєво залежить від обумовленості задачі, тобто задача повинна бути добре обумовленою, а саме, малі зміни початкових умов повинні призводити до малих змін у розв’язку. У протилежному випадку (слабкої стійкості) малі похибки в початкових даних або похибки чисельного методу можуть призводити до великих похибок у розв’язку.

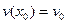Приклад. Рівняння з початковою умовою має розв’язок .

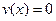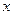При виходить розв’язок . Якщо припустити, що не дорівнює строго нулеві, а має невелике відхилення від нуля, наприклад, , тоді при великих буде мати місце така ситуація.

Якщо , то 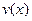при збільшенні 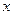прямує до нуля, тобто до незбуреного розв’язку. У цьому випадку розв’язок називається асимптотично стійким за Ляпуновим.

Однак при 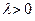зі збільшенням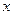 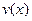необмежено зростає, а саме, наприклад, при .

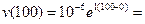
Таким чином, розв’язок виявляється нестійким.

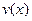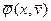Далі будуть розглядатися алгоритми розв’язку задачі Коші на прикладі одного рівняння першого порядку . Узагальнення на випадок системи рівнянь здійснюється заміною на іна , де

, .

 

8.1 Різницева апроксимація диференціальних рівнянь однокроковими методами

Виберемо на відрізку деяку систему , значень аргумента так, щоб виконувалися співвідношення 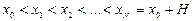. Множину називають сіткою, точки 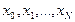— вузлами сітки, величину 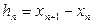- кроком сітки. Якщо 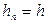, сітка називається рівномірною, в іншому разі - нерівномірною. Сітковою функцією y=y_j=y(x_j) називається функція, що задана у вузлах сітки. Будь-яку сіткову функцію y_j=y(x_j) можна представити у вигляді вектора Y=(y₀, y₁, ..., y_n-1, y_n).

Нехай маємо диференціальне рівняння Lу(x) = f(x,у) (наприклад, 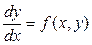) , де L – диференціальний оператор.

Замінимо Lу у вузлі сітки x_i лінійною комбінацією значень сіткової функції y_i на деякій множині вузлів сітки, яка називається шаблоном. Така заміна Lу на L_hy_h називається апроксимацією на сітці диференціального оператора L різницевим оператором L_h. Заміна неперервної функції f(x,у) у вузлах сітки на сіткову функцію f(x_h,y_h) називається апроксимацією правої частини.

У такий спосіб диференціальне рівняння можна апроксимувати (замінити) на сітці різницевою схемою

L_hy_h = f(x_h,y_h) ( наприклад, ).

Вивчення різницевих апроксимацій проводиться спочатку локально, тобто в будь-якому фіксованому вузлі сітки.

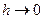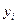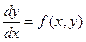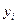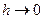При розв’язуванні диференціальних рівнянь чисельним методом основним є питання про збіжність. Стосовно до різницевих методів традиційно більш уживане поняття збіжності при . Позначимо за значення сіткової функції, що відповідає значенню точного розв’язку диференціального рівняння у вузлі - (є наближеними значеннями ). Збіжність при означає таке. Фіксуємо точку 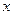і будуємо сукупність сіток 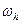таким чином, що 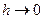і 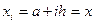(при цьому 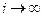). Тоді вважають, що чисельний метод збігається в точці 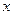, якщо при 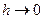, 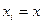. Метод збігається на відрізку 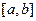, якщо він збігається в кожній точці . Вважають, що метод має -й порядок точності, якщо можна знайти таке число 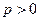, що при .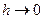

Уведемо далі поняття нев'язки, або похибки, апроксимації різницевого рівняння, що заміняє задане диференціальне рівняння, на розв’язку вихідного рівняння, тобто нев'язка являє собою результат підстановки точного розв’язку рівняння у різницеве рівняння. Наприклад, рівняння 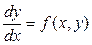можна замінити таким найпростішим різницевим рівнянням

, .

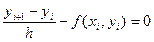Тоді нев'язка визначиться як .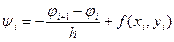

Наближений розв’язок не збігається з 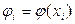, тому нев'язка в -ій точці не дорівнює нулеві.

Чисельний метод апроксимує вихідне диференціальне рівняння, якщо 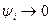при 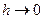, і має -й порядок точності, якщо .

Доведено, що порядок точності чисельного методу розв’язання диференціального рівняння збігається з порядком апроксимації при досить загальних припущеннях.