Метод прогонки

 

Це - ще одна модифікація методу Гауса для систем лінійних алгебраїчних рівнянь спеціального вигляду. Нехай потрібно знайти розв’язок системи так званих триточкових рівнянь:

с₀у₀-b₀y₁=f₀, i=0;

-a_iy_i-1+c_iy_i-b_iy_i+1=f_i, 1£ i£ N-1; (3.8)

-a_Ny_N-1+c_Ny_N=f_N, i=N.

Такі системи виникають як результат апроксимації крайових задач для звичайних диференціальних рівнянь другого порядку, а також при реалізації різницевих схем для рівнянь у часткових похідних.

Переходимо до побудови алгоритму розв’язування системи (3.8). На першому кроці з усіх рівнянь системи (3.8) для i=1,2,...,N виключається за допомогою першого рівняння (3.8) невідоме у₀, потім з перетворених рівнянь для i=2,3, ...,N за допомогою рівняння, що відповідає i=1, виключається невідоме у₁ і т.д. У результаті одержимо одне рівняння відносно у_N. На цьому прямий хід методу закінчується. На зворотному ході для i=N-1,N-2, ...,0 знаходиться у_i через уже знайдені у_i+1, y_i+2, ..., y_N і перетворені праві частини.

Використовуючи підходи методу Гауса, проведемо виключення невідомих з (3.8). Позначивши a₁=b₀/c_0, b₁=f₀/c₀, запишемо (3.8) :

y₀-a₁y₁=b₁, i=0;

-a_iy_i-1+c_iy_i-b_iy_i+1=f_i, 1£ i£ N-1; (3.9)

-a_Ny_N-1+c_Ny_N=f_N, i=N.

Візьмемо перші два рівняння системи (3.9)

y₀-a₁y₁=b₁, -a_iy_i-1+c_iy_i-b_iy_i+1=f_i.

Помножимо перше рівняння на a₁ і додамо до другого рівнянням. Будемо мати (c₁-a₁a₁₎y₁-b₁y₂=f₁+a₁b_1, або після ділення на c₁-a₁a₁

у₁-a₂ у₂= b₂, a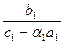₂=, b₂=.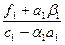

Усі інші рівняння системи (3.9) у₀ не містять, тому на цьому перший крок процесу виключення закінчується. В результаті одержимо нову “скорочену” систему

y₁-a₂y₂=b₂, i=1;

-a_iy_i-1+c_iy_i-b_iy_i+1=f_i, 2£ i£ N-1; (3.10)

-a_Ny_N-1+c_Ny_N=f_N, i=N,

яка не містить невідоме у₀ і має аналогічну (3.9) структуру. Якщо ця система буде розв’язана, то невідоме у₀ знайдеться із рівняння y₀-a₁y₁=b₁. До системи (3.10) можна знову застосувати описаний спосіб виключення невідомих. На другому кроці буде виключене невідоме у₁, на третьому – у₂ і т.д. У результаті l-го кроку одержимо систему для невідомих у_l, y_l+1, ..., y_N

y_l-a_l+1y_l+1=b_l+1, i=l;

-a_iy_i-1+c_iy_i-b_iy_i+1=f_i, l+1£ i£ N-1; (3.11)

-a_Ny_N-1+ c_Ny_N = f_N , i=N.

і формули для знаходження у_i з номерами i£ l-1

у_i=a_i+1 у_i+1+ b_i+1, i=l-1, l-2, ..., 0. (3.12)

Коефіцієнти a_i і b_i знаходяться за формулами

a_i+1=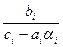, b_i+1=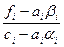, i=1,2,...,

a₁=, b₁=.

Вважаючи в (3.12) l= N-1, одержимо систему рівнянь для y_N і y_N-1

y_N-1-a_N у_N= b_N,

-a_Ny_N-1+ c_Ny_N = f_N ,

з якої знайдемо у_N= b_N+1, y_N-1=a_N у+ b_N.

Таким чином, одержимо остаточні формули для знаходження невідомих

у_i=a_i+1 у_i+1+ b_i+1, i=N-1, N-2, ..., 0,

у_N= b_N+1, (3.13)

де коефіцієнти знаходяться за рекурентними співвідношеннями:

a_i+1=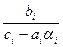, i=1, 2, …, N-1, a₁= (3.14)

b_i+1=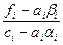, i=1, 2, ..., N-1; b₁= (3.15)

Отже, формули (3.13)-(3.15) описують метод Гауса, що у застосуванні до системи (3.8) одержав спеціальну назву - метод прогонки. Коефіцієнти a_i і b_i називаються прогонковими коефіцієнтами, формули (3.14), (3.15) описують прямий хід прогонки, а (3.13) - зворотний хід. Оскільки значення у_i знаходяться тут послідовно при переході від i+1 до i, то формули (3.13)-(3.15) називають іноді правою прогонкою.

Метод зустрічних прогонок. Аналогічно до правої виводяться формули лівої прогонки:

x_i =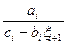, i=N-1, N-2, ..., 1; (3.16)

h_i=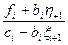, i=N-1, N-2, ..., 0; 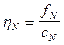, (3.17)

y_i+1=x_i+1 у_i+h_i+1, i=0, 1, ..., N-1; . (3.18)

Тут значення у_i знаходяться послідовно при зростанні індексу i (зліва направо).

Іноді виявляється зручним комбінувати праву і ліву прогонки, одержуючи так званий метод зустрічних прогонок. Цей метод доцільно застосовувати, якщо треба знайти тільки одне невідоме, наприклад y_m (0£m£N), або групу невідомих. Одержимо формули методу зустрічних прогонок. Нехай 1£ m£N і за формулами (3.14)-(3.17) знайдені a₁, a₂, ..., a_m, b₁, b₂, ..., b_m, і x_N, x_N-1, ..., x_m, h_N, h_N-1, ..., h_m. Випишемо формули (3.13), (3.18) для зворотного ходу правої і лівої прогонок для i=m-1. Будемо мати систему, з якої знайдемо y_m

y_m=.

Використовуючи знайдене y_m, за формулами (3.13) для i=m-1, m-2, ..., 0 знайдемо послідовно y_m-1, y_m-1, ..., y₀, а за формулами (3.18) для i=m, m+1, ...,N обчислимо інші y_m+1, y_m+2, ...,y_N.

Отже, формули методу зустрічних прогонок мають вигляд:

a_i+1=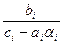, i=1, 2, ..., m-1, a₁=,

b_i+1=, i=1, 2, ..., m-1, b₁=,

x_i =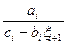, i=N-1, N-2, ..., m, , (3.19)

h_i=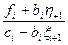, i=N-1, N-2, ..., m, ,

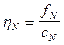для обчислення прогонкових коефіцієнтів і

у_i=a_i+1 у_i+1+ b_i+1, i=m-1, m-2, ..., 0;

у_i+1=x_i+1 у_i+h_i+1, i=m ,m+1, ..., N-1; (3.20)

y_m=

для визначення розв’язків.

3.5 Ітераційні методи розв’язання СЛАР.

Метод простих ітерацій

При великій кількості рівнянь прямі методи розв’язання СЛАР (за винятком методу прогонки) стають важко реалізованими на ЕОМ насамперед через складність зберігання й обробки матриць великої розмірності. У той же час характерною рисою багатьох СЛАР, що виникають у прикладних задачах є розрідженість матриць. Число ненульових елементів таких матриць є малим у порівнянні з їхньою розмірністю. Для розв’язання СЛАР з розрідженими матрицями краще використати ітераційні методи.

Методи послідовних наближень, у яких при обчисленні наступного наближення розв’язку використовуються попередні, уже відомі наближення розв’язку, називаються ітераційними (дивись 2.4).

Розглянемо СЛАР (3.1) з невиродженою матрицею (det A ≠ 0). Розв’яжемо систему (3.1) щодо невідомих при ненульових діагональних елементах a_ii≠ 0, i= 1…n (якщо який-небудь коефіцієнт на головній діагоналі дорівнює нулю, досить відповідне рівняння поміняти місцями з будь-яким іншим рівнянням). Одержимо систему у вигляді

(3.26)

або у векторно-матричній формі X=β+αX.

Тут .

Вирази для компонентів вектора β та матриці α еквівалентної системи:

(3.27)

При такому способі приведення вихідної СЛАР до еквівалентного вигляду метод простих ітерацій ще називають методом Якобі.

За нульове наближення X⁽⁰⁾ вектора невідомих візьмемо вектор правих частин X⁽⁰⁾=β або (x₁^(0),x₂⁽⁰⁾,…,x_n⁽⁰⁾)^*=(β₁,β₂,…,β_n)*. Тоді метод простих ітерацій набере вигляду

(3.28)

З (3.28) бачимо перевагу ітераційних методів у порівнянні, наприклад, з розглянутим вище методом Гауса. В обчислювальному процесі беруть участь тільки добутки матриці на вектор, що дозволяє працювати тільки з ненульовими елементами матриці, значно спрощуючи процес зберігання й обробки матриць. При цьому не відбувається накопичення похибки заокруглення.

Визначення збіжності ітераційного процесу можна знайти в 2.3-2.5. З огляду на сформульовані там теореми, має місце достатня умова збіжності методу простих ітерацій для СЛАР.

Теорема. Метод простих ітерацій (3.28) збігається до єдиного розв’язку СЛАР(3.26)(а отже, й до розв’язку вихідної СЛАР (3.1)) при будь-якому початковому наближенні Х⁽⁰⁾, якщо яка-небудь норма матриці еквівалентної системи менше одиниці ║║‹1.

Якщо ж розглядати СЛАР у вигляді (3.1), то достатньою умовою збіжності є діагональна перевага матриці А, тобто 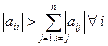(для кожного рядка матриці А модулі елементів, що розміщені на головній діагоналі, більше суми модулів недіагональних елементів). Очевидно, що в цьому випадку менше одиниці й, отже, ітераційний процес (3.28) збігається.

При виконанні достатньої умови збіжності оцінка похибки розв’язку на k – й ітерації дається виразом

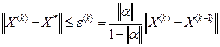, (3.29)

де X* - точний розв’язок СЛАР.

Процес ітерацій зупиняється при виконанні умови e^(к)£e , де e - задана точність розв’язку.

Беручи до уваги, що з (3.29) випливає нерівність

,

можна одержати апріорну оцінку необхідного для досягнення заданої точності числа ітерацій. При використанні за початкове наближення вектора b будемо мати нерівність

,

звідки отримаємо апріорну оцінку числа ітерацій k при

.

Варто підкреслити, що ця нерівність дає завищене число ітерацій k, тому рідко використовується на практиці.

Зауваження. Оскільки є тільки достатньою (не необхідною) умовою збіжності методу простих ітерацій, то ітераційний процес може збігатися іноді, незважаючи на невиконання умови.

Приклад.Методом простих ітерацій розв’язати СЛАР з точністю ε =0,01.

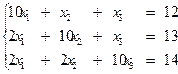
Розв’язання. Приведемо СЛАР до еквівалентного вигляду

або X=β+αX, де

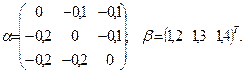
Визначимо 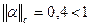. Отже, достатня умова збіжності методу простої ітерації виконана.

Ітераційний процес має в такий вигляд:

Таким чином, обчислювальний процес завершений за 4 ітерації. Відзначимо, що точний розв’язок СЛАР в цьому випадку відомий Х*=(1,1,1)^*. Звідси випливає, що задану точність ε=0,01 задовольняло наближення, отримане вже на третій ітерації.

Відзначимо, що апріорна оцінка необхідної кількості ітерацій дає k+1≥(-2+lg0,6-lg1,4)/lg0,4=5,95, тобто для досягнення точності ε=0,01, відповідно до апріорної оцінки, необхідно зробити не менше п'яти ітерацій, що ілюструє характерну для апріорної оцінки тенденцію до завищення числа ітерацій.

3.6 Метод Зейделя розв’язання СЛАР

Метод простої ітерації досить повільно збігається. Для його прискорення існує метод Зейделя. Суть його в тому, що при обчисленні компонентів х_і^(к+1) вектора невідомих на (k+1)-ій ітерації використовуються х₁^(к+1), х₂^(к+1),...,х_і-1^(к+1), уже обчислені на (k+1)-ій ітерації. Значення інших компонентів беруться з попередньої ітерації. Так само, як і у методі простих ітерацій, будується еквівалентна СЛАР (3.26) і за початкове наближення береться вектор правих частин X⁰=(β₁,β₂,…, β_n)^*.

Тоді метод Зейделя для пошуку наближення Х^(к+1) має вигляд

Із цієї системи бачимо, що Х^k+1=β+BХ^k+1 +CХ^k , де В - нижня трикутна матриця з діагональними елементами, що дорівнюють нулю, а C - верхня трикутна матриця з діагональними елементами, відмінними від нуля, α=В+С. Отже, ,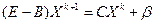

звідки .

Таким чином, метод Зейделя є методом простих ітерацій з матрицею правих частин =(E-B)^-1C і вектором правих частин (E-B)^-1β, й, отже, збіжність і похибку методу Зейделя можна досліджувати за допомогою формул, виведених для методу простих ітерацій, у яких замість матриці підставлена матриця (E-B)^-1C, а замість вектора правих частин - вектор (E-B)^-1β. Для практичних обчислень важливо, що як достатні умови збіжності методу Зейделя можуть бути використані умови, наведені вище для методу простих ітерацій (або, якщо використовується еквівалентна СЛАР у формі (3.1), -діагональна перевага матриці А). У випадку виконання цих умов для оцінки похибки на k -ій ітерації можна використати вираз

.

Відзначимо, що, як і метод простих ітерацій, метод Зейделя може збігатися й при порушенні умови .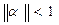

Приклад. Методом Зейделя розв’язати СЛАР із попереднього прикладу.

Розв’язання. Діагональна перевага елементів вихідної матриці СЛАР гарантує збіжність методу Зейделя.

Ітераційний процес будуємо в такий спосіб:

Таким чином, уже на другій ітерації похибка 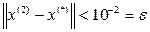, тобто метод Зейделя в цьому випадку збігається швидше ніж метод простих ітерацій.

Приклад .Розв’язання СЛАРAx=b, отримане за допомогою вбудованої функції lsolve (пакет Mathcad).

Перевірка достатньої умови збіжності методу Зейделя

Достатня умова виконана.

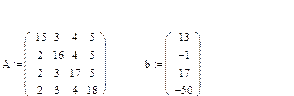
Перетворення системи Ax=b до вигляду x=Bx+c, зручного для ітерацій.

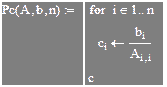
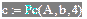
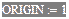- нумерація масивів починається з одиниці.