Машинна арифметика

ВЕОМ для кодування дійсних чисел використовується двійкова система зчислення й прийнята форма подання чисел із плаваючою точкою ,, . Тут 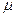- мантиса ; - двійкові цифри, причому завжди =1, p-ціле число, що називається двійковим порядком. Кількість t цифр, що приділяється для запису мантиси, називається розрядністю мантиси. Діапазон подання чисел в ЕОМ обмежений кінцевою розрядністю мантиси й значенням числа p. Усі числа, що подані в ЕОМ, задовольняють нерівності: , де , . Усі числа, за модулем більші , не подані в ЕОМ і розглядаються як машинна нескінченність. Усі числа, за модулем менші 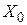, для ЕОМ не відрізняються від нуля й розглядаються як машинний нуль. Машинним іпсилоном 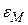називається відносна точність ЕОМ, тобто границя відносної похибки подання чисел в ЕОМ. Покажемо, що . Нехай , тоді границя абсолютної похибки подання цього числа дорівнює . Оскільки , то величина відносної похибки подання оцінюється так:

.

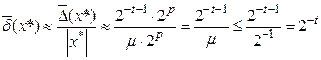Машинний іпсилон визначається розрядністю мантиси та способом округлення чисел, реалізованим на ЕОМ.

Візьмемо такі способи визначення наближених значень параметрів, необхідних у задачі:

1 Покладемо , де n - перше натуральне число, при якому відбувається переповнення.

2 Покладемо 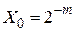, де m – перше натуральне число , при якому збігається з нулем.

3 Покладемо , де k – найбільше натуральне число, при якому сума обчисленого значення 1+ 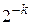ще більша за 1. Фактично 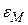є границя відносної похибки подання числа .

Приклад. Для пакета MATHCAD знайти значення машинного нуля, машинної нескінченності, машинного іпсилон.

Машинна нескінченність .

Машинний нуль .

Машинний іпсилон .

; ;

; .

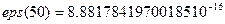Результати обчислювального експерименту:

Машинна нескінченність 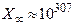.Машинний нуль . Машинний іпсилон .

1.7 Обумовленість обчислювальної задачі

Під обумовленістю обчислювальної задачі розуміють чутливість її розв’язку до малих похибок вхідних даних. Нехай установлена нерівність 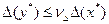, де 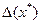- абсолютна похибка вхідних даних, а - абсолютна похибка розв’язку. Тоді 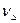називається абсолютним числом обумовленості задачі. Якщо ж установлена нерівність 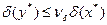між відносними похибками даних і розв’язку, то називають відносним числом обумовленості задачі.

Як правило, під числом обумовленості 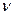розуміють відносне число обумовленості. Якщо , то задачу називають погано обумовленою.

Як уже зазначалося основними джерелами похибок в обчислювальних задачах є помилки у вихідних даних, помилки округлення під час машинних обчислень і обмеження точності використовуваної обчислювальної схеми (відмінність обчислювальної схеми від чисельного методу цілком символічна – у випадку класичних завдань чисельного аналізу ми говоримо про чисельний метод, схему ж чисельного розв’язку конкретної прикладної задачі називаємо обчислювальною схемою). Похибки, що виникають через помилки у вхідних даних, і похибки, пов’язані з округленнями, є неусувними з погляду обчислювача. У той же час при конструюванні обчислювальної схеми ми маємо деяку свободу у виборі використовуваних чисельних методів, які відрізняються один від одного точністю та стійкістю.

Точність чисельного методу, як правило, визначається порядком використовуваного в ньому наближення. Наприклад, при інтегруванні замість методу прямокутників можна використовувати метод парабол , що має більш високий порядок і забезпечує кращу точність. Часто також у нашому розпорядженні є параметр, що дозволяє керувати точністю одержуваного розв’язку (у випадку чисельного інтегрування це крок інтегрування). Точність обчислювальної схеми, як правило, обирають так, щоб відповідна похибка була принаймні вдвічі меншою за неусувну похибку у вхідних даних.

Важливо також розуміти значення стійкості використовуваної обчислювальної схеми. Похибки у вхідних даних і похибки округлення можуть по-різному впливати на точність результату залежно від використовуваної схеми обчислень. Під стійкістю обчислювальної схеми розуміють її стійкість стосовно похибок у вхідних даних і похибок округлення – для стійкої схеми малі похибки в даних і типові похибки округлення не призводять в остаточному підсумку до більших похибок. У той же час використання нестійкої обчислювальної схеми може призвести до значного зростання похибки результату.

Нестійкість також може мати різну природу. Іноді нестійкість обумовлена сутністю розв’язуваної задачі. У цьому випадку говорять, що задача погано обумовлена або некоректна. Більшість так званих обернених задач є прикладом поганої обумовленості. У той же час навіть у випадку коректної (добре обумовленої) задачі невдалий вибір обчислювальної схеми може призвести до нестійкості. Отже,

· нестійкість може бути властива завданню (слабка обумовленість);

· навіть добре обумовлену задачу можна зіпсувати невдало підібраним чисельним методом.

 

1.8 Приклад втрати точності

Іноді втрата точності під час розв’язання задачі виявляється неминучою. Класичний приклад – пошук екстремуму функції.

Розглянемо задачу мінімізації функції 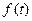і припустимо, що мінімум досягається в точці t₀. В околі такої точки збільшення df функції 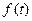при збільшенні аргумента t на мале dt виражається так:

,

оскільки 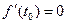. Таким чином, в околі екстремуму збільшення функції пропорційно квадрату збільшення аргумента. З цього випливає принципова неможливість локалізувати екстремум точніше, ніж із половиною доступних значущих цифр – менші зміни аргумента не будуть приводити до помітної зміни значення функції.

Часто при розв’язанні рівняння пропонується перейти до еквівалентної задачі пошуку мінімуму функції . Якщо мінімум досягається в точці t₀ і дорівнює нулю, то в цій точці рівняння має корінь. Легко зрозуміти, чому без достатніх підстав не варто застосовувати цей метод. Для лівої частини рівняння в околі простого кореня ми маємо представлення 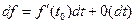і можемо локалізувати корінь із точністю, що збігається з точністю використовуваної машинної арифметики.

1.9 Погана обумовленість задачі

Погано обумовлені задачі є з погляду обчислювача великою проблемою. У таких задачах неминучі помилки округлення й похибки у вхідних даних катастрофічно наростають, роблячи одержувану відповідь неприйнятною. Погано обумовлені задачі становлять небезпеку при отриманні числового розв’язку. Потрібно вміти виявляти погану обумовленість і боротися з нею.

Відмінна риса погано обумовлених задач така: мале відхилення у вхідних даних призводить до суттєвих змін відповіді. Якщо розглядати результат обчислень як функцію y(x) від вхідних даних, то мале відхилення dx аргумента приведе до зміни обчисленого значення на dy, причому |dy| можна оцінити як добуток модуля похідної та абсолютної величини відхилення: 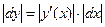. У випадку поганої обумовленості малі зміни аргументу (вхідних даних) приводять до суттєвих змін у відповіді, тобто похідна набуває більших за модулем значень. Як правило, працюють із відносними приростами

Dx = dx/x, Dy = dy/y.

У цьому випадку 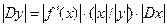. Число називається числом обумовленості задачі. Отже,

або .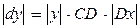

Якщо помилки у вихідних даних обумовлені винятково використанням машинної арифметики, то 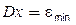, де – точність машинної арифметики. Машинним іпсилоном називається мінімальне додатне число, що при додаванні до числа 1.0 дає результат, більший ніж 1.0. Величина машинного іпсилона визначає відносну похибку введених чисел і, таким чином, є найважливішою характеристикою машинної арифметики. У цьому випадку і . 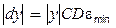Таким чином, чим більше число обумовленості, тим сильніший вплив похибки вхідних даних і похибки, внесеної округленнями.

Іноді дуже прості задачі демонструють погану обумовленість.

Приклад. Розглянемо задачу знаходження кореня многочлена

f(t)=(t-2)⁹=t⁹–18t⁸+144t⁷–672t⁶+2016t⁵–4032t⁴+5376t³–4608t²+2304t–512.

Якщо многочлен заданий за допомогою першої з наведених формул, то задача знаходження кореня не становить проблеми. Нехай многочлен заданий за допомогою іншої формули, тобто задані його коефіцієнти й відомо, що один із коренів локалізований на відрізку [1,3]. Тоді значення многочлена можна обчислювати за схемою Горнера

f(t) = ((((((((t – 18)t + 144)t – 672)t + 2016)t –4032)t + +5376)t – 4608)t + 2304)t – 512,

а корінь можна знайти за методом дихотомії. Розглянемо поведінку функції на відрізку [1.97,2.03]. Обчислення виконувалися з подвійною точністю (double). Значення функції обчислювалися із кроком 0.0001. На першому малюнку показані результати при обчисленні за першою з наведених формул, а на другому – при обчисленні за схемою Горнера.

Рис. -1.1

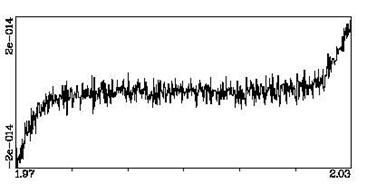
Рис. -1.2

Бачимо, що в околі точки t=2 функція, обчислена за схемою Горнера, поводиться непередбачувано. Якщо ми спробуємо знайти чисельно корінь рівняння f(t) = 0 для функції f(t), що обчислюється за схемою Горнера, то одержимо випадкову точку з відрізка [1.98, 2.02]. На цьому відрізку зміна функції становить менш ніж 4e-14, але відрізок невизначеності для кореня виходить великий – довжиною 0.04.

Обмежимося простим і нестрогим зауваженням, що з’ясовує природу поганої обумовленості цієї задачі. Якщо точка t пробігає діапазон [2-e,2+e] при деякому досить малому значенні e (наприклад, при e<0.01), то значення функції f(t) змінюється дуже мало. Відповідно, мала зміна функції f(t) (або коефіцієнтів многочлена) приведе до великої зміни значення кореня.

 

1.10 Прості тести на обумовленість

У погано обумовленій задачі відповідь дуже залежить від будь-яких похибок як у вхідних даних, так і внесених у процесі обчислень. Це дозволяє використовувати наступні прості тести на погану обумовленість.

·Можна спробувати змінити вхідні дані, вносячи в них малі випадкові помилки. У випадку поганої обумовленості відповідь повинна при цьому суттєво змінюватися.

·Можна спробувати повторити розрахунок з використанням машинної арифметики різної точності. Саме із цього погляду корисно визначати свій дійсний тип так, щоб зміна точності арифметики зводилася просто до перекомпіляції. Сильна залежність відповіді від точності використовуваної арифметики свідчить про слабку обумовленість.

·Можна внести штучну похибку у деякі із проміжних результатів. Для цього можна просто округляти обчислені значення до заданої кількості значущих цифр.

 

1.11 Загальна схема розв’язання задач чисельного аналізу. Апроксимація, стійкість, збіжність

Більшість задач чисельного аналізу в загальному вигляді можна записати у вигляді рівняння

y=F(x), (1.11)

де F:XàY ¾ деякий оператор, що задає відображення метричного простору Х у метричний простір У( дивись Додаток 1.1).

Загальний підхід, що реалізується в наближених методах розв’язання таких задач, полягає в заміні рівняння (1.11) близьким йому, простішим (як правило, скінченновимірним) рівнянням

у_n=F_n(x_n) . (1.12)

Тут F_n:X_nàY_n – оператор, що відповідає вихідному оператору F. При цьому елементи x_n є X_n та y_n є Y_n розглядаються як образи елементів x є X та y є Y. Цей роз’язок можна визначити через відповідні оператори

x_n=j(x), y_n=y(y) . (1.13)

Як відомо, заміна одних математичних об’єктів іншими, чимось близькими до них, називається апроксимацією.

Визначення 1 Рівняння

F_n(x_n)=yn(y) (1.14)

апроксимує рівняння 1.11 (оператор F_n апроксимує F), якщо для будь-яких елементів х з D(F)ÍX міра апроксимації

r_yn(F_n(j_n(x)),y_n(F(x)))® 0 , коли nൠ. (1.15)

(Тут r_yn(a,b)) визначає метрику, тобто відстань між елементами a,bÎY_n ).

Щоб можна було порівнювати якість різних моделей вигляду (1.14) для задачі (1.11), користуються поняттям порядку апроксимації. Ця характеристика пов’язує прямування до 0 міри апроксимації (1.15) з порядком зменшення деякої залежної від n малої величини, наприклад, кроку апроксимації.

Будемо вважати, що розв’язки х*ÎХ, та рівнянь відповідно (1.11) та (1.14) існують і єдині. Наближеним розв’язком задачі (1.11) вважається елемент , де обернене до відображення .

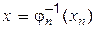Головним питанням будь-якої теорії наближених методів розв’язання задач вигляду (1.11) є питання про те, чи можна наближеним розв’язком х⁽ⁿ⁾ як завгодно добре відобразити поведінку точного розв’язку х*. Це питання про збіжність х⁽ⁿ⁾ до х*.

Визначення 2 Має місце збіжність наближеного розв’язку х⁽ⁿ⁾ до точного розв’язку х* рівняння (1.11), якщо

.

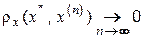Наявність фактичних оцінок величин 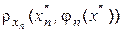дозволяє не тільки робити висновки про збіжність наближених розв’язків, але і визначати похибки отриманих наближень до розв’язку.

Питання про збіжність розв’язків у⁽ⁿ) до у* тісно пов’язане з тим, чи можна надійно розв’язати спрощену задачу (1.14). Адже спрощена задача також розв’язується наближено. Покращання якості апроксимації шляхом зменшення її міри (1.15) спричинює збільшення розмірності n для задачі (1.14), а отже, збільшення об’єму обчислень, що може призвести до збільшення обчислювальних похибок .

Визначення 3 Обчислювальний процес називається стійким, якщо малі похибки вхідних даних викликають малі похибки результатів.

 

Питання і завдання до розділу 1

 

1 Джерела й класифікація похибок. Наближені числа. Абсолютна й відносна похибки. Правильні й значущі цифри. Способи округлення.

2 Подання чисел в ЕОМ. Машинний нуль, машинна нескінченність, машинний іпсилон. Алгоритми обчислення.

3 Похибки арифметичних операцій над наближеними числами.

4 Похибки обчислення функцій однієї та декількох змінних.

5 Похибки обчислення неявно заданої функції.

6 Числа 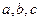задані наближено:
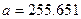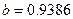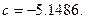,,Відомо, що 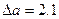,,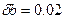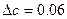. Записати ці числа з усіма правильними знаками.

7 Наближене число a містить 5 правильних цифр. Що можна сказати про відносну похибку числа a?

8 З якою відносною похибкою потрібно знайти наближене значення числа a, щоб правильними виявилися 5 значущих цифр?

9 Для наближених чисел a та b (a>b>0) відомо, що (a)=(b)=. Оцінити похибки:
а) (a+b), b) ,(a-b), c) (a*b), d) (a/b).

10 Числа a та b задані наближено: , , 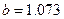. Оцінити похибки:
a)різниці , b) добутку .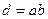
Записати відповідь з урахуванням правильних цифр.

11 Визначити правила оцінки абсолютних і відносних похибок функцій

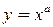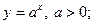a); b) c) .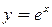

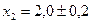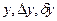12 Функція обчислюється при значеннях , , . Знайти значення . Записати результат з усіма правильними цифрами.

13 Коефіцієнти 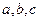обчислюються з відносною похибкою (a)=(b)=(с)=. Знайти максимальну похибку, з якою можуть обчислюватися корені рівнянь: a) ; b) .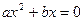

14 Функція 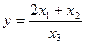обчислюється при значеннях , ,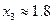. Визначити при яких значеннях 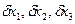відповідь буде містити 3 правильні цифри.

Розділ 2

Числове розв’язання нелінійних рівнянь

У традиційних курсах математики найчастіше ставиться задача пошуку точного розв’язку таких рівнянь. Однак у прикладних задачах виникають такі рівняння, коли, як правило, неможливо його знайти .

Якщо обчислювальна техніка дозволяє впоратися з великою кількістю складних рівнянь, то абстрактні методи дозволяють для різноманітних класів рівнянь (таких, як алгебраїчні, диференціальні, інтегродиференціальні і т.д.) знайти загальні підходи до їх розв’язку.

Спробуємо дати уявлення про деякі результати, пов'язані з питаннями існування і побудови розв’язків нелінійних рівнянь. Визначимося з математичним апаратом, необхідним для обґрунтування чисельних методів розв’язання рівнянь.

 

2.1 Відображення множин

 

Бажання охопити якнайбільше рівнянь призводить до необхідності розглядати відображення (функції), за допомогою яких записуються рівняння досить загальної природи, і застосовувати теоретико-множинний підхід. Для цього залучимо поняття відображення однієї множини в іншу, причому із самого початку підкреслимо, що це поняття буде вважатися первинним, що не підлягає формально строгому визначенню (так само, як і поняття числа, точки, множини і т.д.). Інтуїтивний зміст слова "відображення" відбиває наявність відповідності між елементами двох множин (при бажанні можна обмежитися тільки розглядом числових множин).

Нехай: 1) задана (непуста) множина X; 2) задана непуста множина Y; 3) для кожного елемента множини X зазначений один цілком визначений елемент множини Y. У такому випадку будемо говорити про відображення множини X у множину Y.

Інакше кажучи, поняття "відображення" містить у собі нероздільний опис двох множин X (область визначення відображення), Y (область значення) і опис правила (способу, закону), за яким для кожного елемента х з множини X задається певний елемент у з множини Y, у який елемент х відображається.

Закон (правило) відповідності, за яким для кожного елемента області визначення множини відображення X задається рівно один елемент області значень Y, позначимо буквою f. Тоді відображення множини Х у множину Y можна записати так (це позначення прийняте в сучасній математиці):

чи . (2.1)

Елемент y є Y, у який при даному відображенні (2.1) переходить елемент х є X, називається образом елемента х (чи значенням відображення на елементі х) і позначається символом f(x). Часто, коли ясний вибір множин X і Y, для розглянутої функції використовується позначення f.

З'ясувавши зміст поняття "відображення", можна дати визначення функції: функцією називається однозначне відображення однієї множини чисел в іншу множину чисел. Таким чином, функція — той окремий випадок відображення, коли область визначення й область значень є числовими множинами.

 

2.2 Розв’язок рівнянь і нерухомі точки відображень

 

Одна з простих теорем існування розв’язку формулюється так:

Теорема 1Нехай f: [а, b] ® R — неперервна на відрізку [а, b] функція і f(a)f(b)< 0 (тобто на кінцях відрізків вона набуває значення різних знаків), тоді рівняння

f(x)=0 (2.2)

має на відрізку [а, b] хоча б один розв’язок.

Теореми існування, як правило, формулюють як теореми існування нерухомих точок відображень.

Нехай f: X® X— деяке відображення множини Х в себе. Елемент х₀ з X називається нерухомою точкою відображення f, якщо має місце рівність f(x₀) = х₀.

Якщо f: [а, b] ® R — функція, що задовольняє умови теореми 1, то розглянемо на відрізку [а, b] функцію F(x) = lf(x)+х, де параметр l виберемо так, щоб усі значення функції F належали відрізку [а, b]. Наприклад, можна покласти l=М/m,

де М=maxf(x)=f(x₂) і m = min f(x) = f(x₁),

^{xє[a,b] xє[a,b]}

x₁ і x₂ — точки з відрізка [а, b], у яких досягаються мінімум і максимум функції f відповідно.

Безпосередньо з вигляду функції F випливає, що х₀ — розв’язок рівняння (2.2) тоді і тільки тоді, коли х₀ — нерухома точка для функції f. Таким чином, теорема 1 еквівалентна теоремі, що формулюється у вигляді принципу нерухомої точки.

Теорема2 Неперервне відображення F відрізка в себе має нерухому точку.

Аналогічно задачу про можливість розв'язання систем рівнянь з кількома невідомими можна звести до питання існування нерухомої точки відображення багатомірного куба (чи кулі) у себе.

Крім проблеми існування нерухомої точки, виникає природне запитання про способи її наближеного обчислення. У наступній теоремі одночасно вирішуються обидві проблеми.

Теорема 3Нехай j: [а, b] ® [а, b] — функція, що задовольняє умову: існує число q з інтервалу (0,1) таке, що

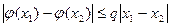(2.3)

для всіх чисел х₁,х₂ з [а, b]. Тоді функція j має єдину нерухому точку x^*є[а, b], що є границею послідовності х₀, х₁,х₂,..., де х₀ — довільна точка з [а,b], а інші члени послідовності визначаються за правилом:

х_n = j (х_n-1), n > 1.

Викладений у теоремі метод побудови нерухомої точки називається методом простих ітерацій або методом послідовних наближень, а послідовність {х_n} — ітераційною послідовністю.

 

2.3 Теореми про стискаючі відображення

 

Розглянемо повний метричний простір Х з відстанню r. Відображення f: X®X називається стискаючим, якщо існує таке число q є (0, 1), що

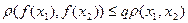(2.4)

для всіх елементів х₁, х₂ є X.

Має місце наступне узагальнення теореми 3.

Теорема 4(про стискаючі відображення). Стискаюче відображення f: X®X має єдину нерухому точку х^* є X, яку можна знайти як границю послідовності

(2.5)

де х₀ — довільний елемент із X. Крім того виконується

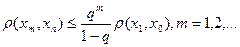(2.6)

Доведення.Покажемо, що послідовність {х_n} фундаментальна. З (2.4) і (2.5) одержуємо оцінки

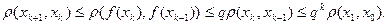
Вважаючи для визначеності, що n>m, з нерівності трикутника одержуємо оцінки

при m®∞.

Таким чином, побудована послідовність {х_n} фундаментальна. Оскільки метричний простір X повний, то вона має границю х* є X. Оскільки

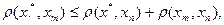
то при n®∞ з наведених оцінок одержуємо доведену оцінку (2.6). Оскільки при m®∞

то f(x)= x^* , тобто x^* — нерухома точка відображення f.

Доведемо, що вона — єдина. Нехай x^** — інша нерухома точка для f. Тоді з оцінки

випливає, що r( x^*, x^**) = 0 і тому x^* = x^**.

Теорема доведена.

Нерівність (2.6) дозволяє визначити, скільки потрібно знайти послідовних наближень, щоб знайти нерухому точку x^* відображення f із заданою точністю e>0. Наприклад, нерівність r( x^*, х_m) <e буде виконана, якщо

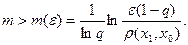
Теорема 4 широко застосовується для пошуку розв’язків систем алгебраїчних, диференціальних та інтегральних рівнянь, а також покладена в основу різних методів, які використовуються в обчислювальній математиці.

 

2.4 Критерій існування нерухомих точок

 

Розглянемо узагальнення теорем 1 і 2, що пов'язані з питаннями існування нерухомих точок відображень. Формулювання відповідних результатів використовує наступні важливі поняття.

Множина К з метричного простору X, на якому введена відстань r, називається компактною, якщо з будь-якої послідовності {х_n} елементів цієї множини можна виділити підпослідовність, що збігається, границя якої також належить К.

Множина В з лінійного простору X (тобто множина, на якій визначені операції додавання і множення на числа з R) називається опуклою, якщо разом з будь-якими двома точками х₁, х₂єВ множині В належать усі точки ах₁+(1-а)х₂, а[0,1] (множина таких точок називається відрізком, що з'єднує точки х₁, x₂єВ).

Теорема5. Будь-яке неперервне відображення f: К®К опуклої компактної множини К з лінійного простору Rⁿ має нерухому точку.

Ця теорема доведена голландським математиком Л.Э.Я. Брауером. Оскільки будь-який відрізок [а, b] з R є опуклою компактною множиною, то теорема 2 випливає з теореми Брауера. Розглянемо деякі наслідки теореми 5.

Теорема Бореука-Улама для кола.Нехай f: С®R — функція на колі С. Тоді існує пара точок-антиподів х, х* така, що f(х) =f(x*).

Наслідком цієї теореми є той факт, що на будь-якому колі Земної кулі (наприклад, на екваторі) знайдеться пара

антиподів, у яких температура повітря однакова.

Теорема(про млинці). Якщо А і В — обмежені фігури на площині, то існує пряма, що поділяє кожну з цих фігур на дві рівновеликі за площею частини.

Тут передбачається, що кожна фігура має площу (що може бути тоді, коли фігура має складну форму). Образно кажучи, теорема стверджує, що два млинці, що лежать на тарілці, можна розрізати точно навпіл одним змахом ножа.

Теорема Брауера має різноманітні узагальнення, що знаходять застосування в питаннях існування розв’язків диференціальних та інтегральних рівнянь, у математичній економіці (теорія економічної рівноваги) і теорії ігор.

 

2.5 Розв’язання нелінійних рівнянь

у комплексній площині

 

Нехай задана функція f(х) дійсної змінної. Потрібно знайти нулі функції f(х) або, що те ж саме, корені рівняння

f(x)=0 (2.7)

Уже на прикладі алгебраїчного многочлена відомо, що нулі f(х) можуть бути як дійсними, так і комплексними. Тому більш точною є постановка задачі у визначенні коренів рівняння (2.7), розміщених у заданій області комплексної площини. Можна розглядати задачу визначення дійсних коренів, розміщених на заданому відрізку. Іноді, нехтуючи точністю формулювань, будемо говорити, що потрібно розв’язати рівняння (2.7).

У загальному випадку задача визначення коренів рівняння (2.7), як правило, розв’язується в два етапи. На першому етапі вивчається розміщення корені і проводиться їх відділення, тобто виділяються області в комплексній площині, що містять тільки один корінь. Крім того, вивчається питання про кратність коренів. Знаходяться деякі початкові наближення для коренів рівняння (2.7). На другому етапі, використовуючи задане початкове наближення, будується ітераційний процес, що дозволяє уточнити значення невідомого кореня.

Не існує якихось загальних регулярних прийомів розв’язання задачі про розміщення коренів довільної функції f(х). Найбільш повно вивчене питання про розміщення коренів алгебраїчних многочленів

f(x)=a₀+a₁x+a₂x²+…+a_mx^m. (2.8)

Наприклад відомо, що якщо для многочлена (2.8) з дійсними коефіцієнтами виконані нерівності f(c)>0,f’(c)>0,…,f^(m)(c)>0, то додатні корені f(х) не перевершують числа с. Дійсно, з формули Тейлора

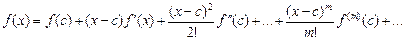
одержуємо, що f(x)>0 при x>c.

Чисельні методи розв’язання нелінійних рівнянь є, як правило, ітераційними методами, що припускають завдання досить близьких до шуканого розв’язку початкових даних. Перш ніж переходити до викладу конкретних ітераційних методів, відзначимо два прості прийоми відділення дійсних коренів рівняння (2.7). Припустимо, що f(х) визначена і неперервна на [а,b].

Перший прийом полягає в тому, що обчислюється таблиця значень функції f(х) у заданих точках х_kÎ[а, b], k=0, 1,..., п. Якщо виявиться, що при якомусь к числа f(х_k), f(x_k+1) мають різні знаки, то це буде означати, що на інтервалі (х_k,x_k+1) рівняння (2.7) має принаймні один дійсний корінь (точніше, має непарне число коренів на (х_k, x_k+1)). Потім можна розбити інтервал (x_k,x_k+1) на більш дрібні інтервали і за допомогою аналогічної процедури уточнити розміщення кореня.

Більш регулярним способом відділення дійсних коренів є метод бісекції (розподілу навпіл). Припустимо, що на (а, b) роміщений лише один корінь х рівняння (2.7). Тоді f(а) і f(b) мають різні знаки. Нехай для визначеності f(а)>0, f(b)<0. Покладемо x₀=0,5×(a+b) і обчислимо f(x₀). Якщо f(x₀)<0, то шуканий корінь знаходиться на інтервалі (a,x₀), якщо ж f(х₀)>0, то на (х₀, b). Далі, із двох інтервалів (a,x₀) і (х₀,b) вибираємо той, на кінцях якого функція f(х) має різні знаки, знаходимо точку х₁-середину обраного інтервалу, обчислюємо f(х₁) і повторюємо зазначений процес. У результаті одержуємо послідовність інтервалів, що містять шуканий корінь х_1, причому довжина кожного наступного інтервалу вдвічі менша за попередній. Процес закінчується, коли довжина знову отриманого інтервалу стане менше заданого числа e>0, і за корінь х приблизно береться середина цього інтервалу.

Помітимо, що якщо на (а, b) міститься кілька коренів, то зазначений процес зійдеться до одного з коренів, але заздалегідь невідомо, до якого саме. Можна використовувати прийом виділення коренів: якщо корінь х=х^* кратності m знайдений, то розглядається функція g(х)=f(х)/(x-x^*)^т і для неї повторюється процес визначення кореня.

 

y

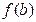
O ax^*b x

Рис. - 2.1

Обмеження кореня функції, якщо вона визначення на необмеженому інтервалі здійснюється так.

1 Для початкового наближення x₀, знайти f₀=f(x₀), задати інтервал пошуку D і його інкремент d>1.

2 Обчислити a=x₀-D, b=x₀+D; f_a = f(a), f_b = f(b).

3 Збільшити інтервал пошуку: D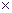=Dd.

4a Якщо знаки f_a і f₀ різні, то вважати корінь обмеженим на [a,x₀] -> вихід.

4b Якщо знаки f_b і f₀ відрізняються, то вважати корінь обмеженим на [x₀,b] -> вихід.

5 Перевіряється, яке з f_a і f_b найменше. Якщо вони однакові, то переходимо до 6a (двосторонній пошук), якщо f_b – робимо пошук вправо 6b, інакше - пошук уліво 6c.

6a Знаходимо a=a-D, b=b+D, f_a=f(a), f_b=f(b), йдемо до пункту 3.

6b Присвоюємо послідовно a=x₀, x₀=b, f_a=f₀, f₀=f_b; знаходимо b=b+D, f_b=f(b), йдемо до пункту 3.

6c. Аналогічно 6b, тільки напрямок пошуку - вліво.

2.6 Метод простих ітерацій

Замінимо рівняння 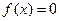еквівалентним йому рівнянням .

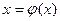y

 

 

 

 

O a x₁ x^* x₀ b x