Непрерывность функции. Точки разрыва. Асимптоты графика функции
Непрерывность функции. Точки разрыва. Асимптоты графика функции
Дифференцирование функций
Правила дифференцирования
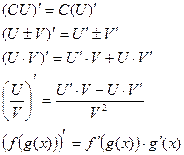
Таблица производных основных функций
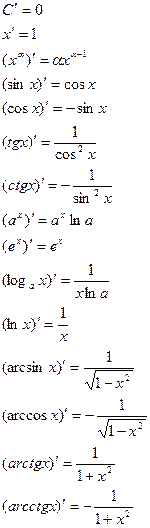
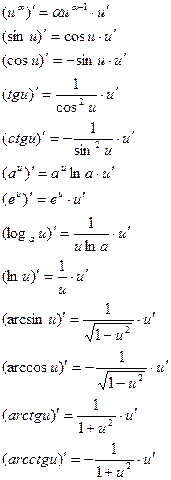
Пример.
а) 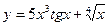

б) 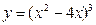
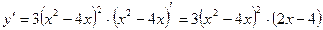
в) 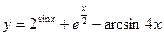
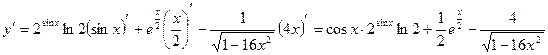
г) 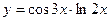

д) 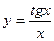
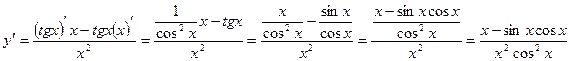
УПРАЖНЕНИЕ:
Найдите производные функций
1)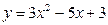
2)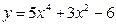
3)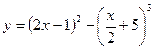
4) 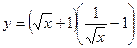
5)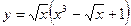
6)
7) 
8) 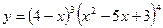
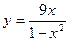
9) 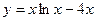
10) 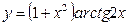
11) 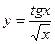
12) 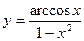
13) 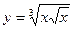
14) 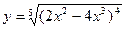
15) 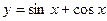
16) 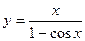
17) 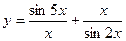
18) 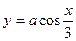
19) 
20) 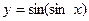
21) 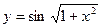
22) 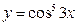
23) 
24) 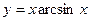
25) 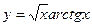
26) 
27) 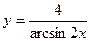
28) 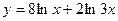
29) 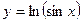
30) 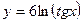
31) 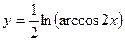
32) 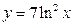
33) 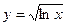
34) 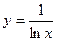
35) 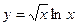
36) 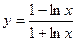
37) 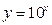
38) 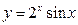

39) 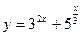
40) 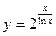
41) 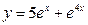
42) 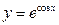
43) 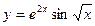
44) 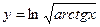
Уравнение касательной и нормали к плоской кривой
Пусть дана кривая L, заданная уравнением . Возьмем на ней фиксированную точку Мо(х0;у0). Если точка М1(х1;у1) тоже принадлежит кривой L, то прямая… М1 стремилась к совпадению с М0 . Предельное положение секущей М0 М1 (если оно… М1 →М0 называется касательной к кривой L в точке М0.Эластичность функции
Будем рассматривать дифференцируемую функцию . Как и ранее, Отношения представляют собой относительные приращения аргумента и функции… Величина показывает, сколько процентов составляет приращение ∆х… Отношение показывает, сколько процентов составит среднее ( на промежутке от х до х+∆х) относительное приращение…Вычисление дифференциала функции
Дифференциалом функции у=f(x) называется произведение производной этой функции на произвольное приращение аргумента : Дифференциал аргумента равен приращению аргумента : . Поэтому дифференциал… Дифференциалом второго порядка называется дифференциал от дифференциала первого порядка: , т.е. дифференциал второго…Приближенные вычисления.
Формулу используют для приближённого вычисления значений функций. Допускаемая при этом погрешность мала при малых значениях , т.е. близких к .… Приближенное вычисление степеней. Рассмотрим функцию . Пусть аргумент х… Пример1Применение производной к исследованию функции
Функция y=f(x) называется возрастающей в промежутке , если для любых и , принадлежащих этому промежутку и таких , что < , имеет место неравенство…Интегральное исчисление. Неопределенный интеграл и его свойства
Определение Пусть функции f(x) и F(x) определены на (a;b). Если функция F(x) имеет производную на (a;b) и для всех х из этого…Основные свойства неопределенного интеграла
2° Из (2) следует 3°Несколько стандартных правил интегрирования
Правило подведения под знак дифференциала. Правило основано на следующем очевидном утверждении, которое следует из инвариантности формы первого дифференциала:…Примеры.
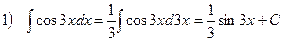 . Здесь воспользовались
. Здесь воспользовались 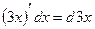

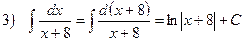

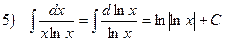
 , так как
, так как 
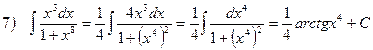
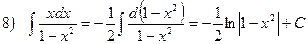
Следует отметить, что рассмотренное правило является частным случаем более общего правила замены переменной.
Правило замены переменной.
Утверждение, на котором основывается предыдущее правило, но записанное в виде
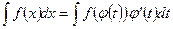 , где
, где 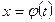 - дифференцируемая функция, множество значений которой является областью определения функции
- дифференцируемая функция, множество значений которой является областью определения функции  . Естественно, как и ранее, мы предполагаем существование всех указанных интегралов. Из этой формулы следует и смысл замены переменной: функцию
. Естественно, как и ранее, мы предполагаем существование всех указанных интегралов. Из этой формулы следует и смысл замены переменной: функцию 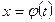 стараются подобрать так, чтобы подынтегральное выражение
стараются подобрать так, чтобы подынтегральное выражение 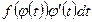 , в полученном после преобразований интеграле, было проще исходного.
, в полученном после преобразований интеграле, было проще исходного.
Примеры.

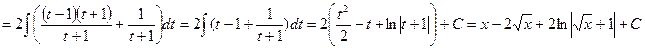
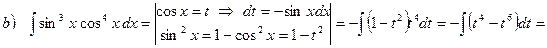
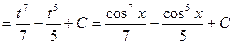 .
.
Правило интегрирования по частям.
Дифференциал произведения двух функций 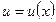 и
и 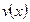 определяется формулой
определяется формулой 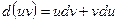 . Перепишем равенство в виде
. Перепишем равенство в виде 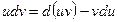 и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:
и проинтегрируем обе части. С учетом свойств интеграла, получим формулу интегрирования по частям:
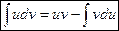
С помощью этой формулы обычно вычисляются интегралы от функций представляющих произведение многочлена на 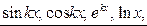 причем в первых трех случаях за
причем в первых трех случаях за  обозначают многочлен, а в последнем
обозначают многочлен, а в последнем  . Поскольку в правой части формулы вместо функции
. Поскольку в правой части формулы вместо функции 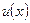 появляется дифференциал этой функции
появляется дифференциал этой функции 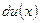 , то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция
, то есть возможность получить интеграл проще, если дифференциал функции проще, чем сама функция. После того как сама функция 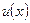 выбрана, оставшееся под интегралом выражение обозначаем
выбрана, оставшееся под интегралом выражение обозначаем  , тогда сама функция
, тогда сама функция 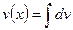 .
.
Примеры.
a) 
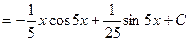
b) 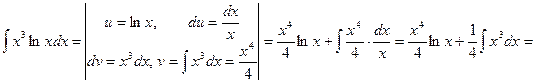
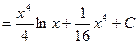
Задания для самоконтроля
*Вычислить интегралы, преобразовав подынтегральную функцию так, чтобы можно было использовать таблицу интегралов.
1. 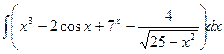
2. 
3. 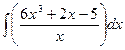
4. 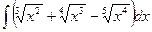
5. 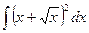
6. 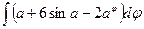
7. 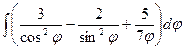
8. 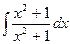
9. 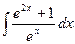
10. 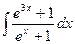
11. 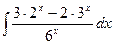
12. 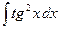
13. 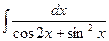
14. 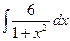
15. 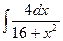
16. 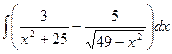
17. 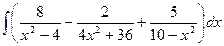
18. 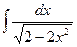
19. 
20. 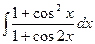
*Вычислить интегралы, используя подходящую замену переменных.
1. 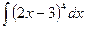
2. 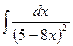
3. 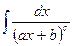
4. 
5. 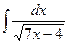
6. 
7. 
8. 
9. 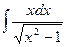
10. 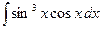
11. 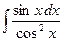
12. 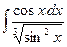
13. 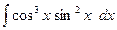
14. 
15. 
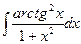
16. 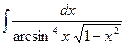
17. 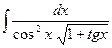
18. 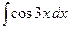
19. 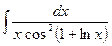
20. 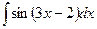
21. 
22. 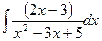
23. 
24. 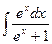
25. 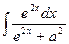
26. 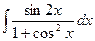
27. 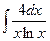
28. 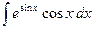
29. 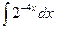
30. 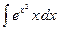
31. 
32. 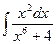
33. 
34. 
35. 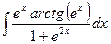
36. 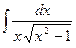
*Вычислить интегралы методом интегрирования по частям
1. 
2. 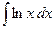
3. 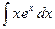
4. 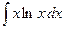
5. 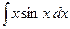
6. 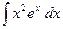
7. 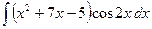
8. 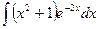
9. 
10. 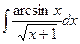
11. 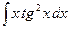
12. 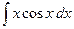
13. 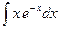
14. 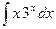
15. 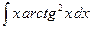
16. 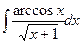
17. 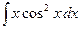
18. 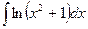
Определенный интеграл
Понятие определенного интеграла. Рассмотрим функцию определенную и непрерывную на некотором отрезке числовой прямой. Разобьем на n отрезков длины…Дифференциальные уравнения
Многие процессы экономики, физики, химии, астрономии, биологии описываются одной функцией у=у(х), заданной на некотором множестве Х или несколькими… Рассмотрим некоторые процессы, математические характеристики которых приводят… Задача 1Дифференциальные уравнения I порядка
Простейшим дифференциальным уравнением I порядка называется дифференциальное уравнение вида (2) , где f(x) – функция, определенная и непрерывная на… Общее решение уравнения (2) может быть записано в виде , где F(x) - одна из… Пример 1.Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида (1)В противном случае- неоднородным.
Рассмотрим сначала способ построения общего решения линейного однородного дифференциального уравнения второго порядка
 (2)
(2)
В теории линейных дифференциальных уравнений доказывается следующее утверждение.
Теорема 1. Общим решением уравнения (2) является функция
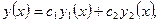 (3)
(3)
Где и - пара произвольных действительных чисел, а и - пара решений уравнения (2), таких, что их частное отлично от постоянной величины.
Мы примем эту теорему без доказательства.
Будем искать решение уравнения (2) в виде 
Теорема 2. Для того чтобы функция являлась решением уравнения (2), необходимо и достаточно, чтобы число являлось корнем уравнения
Доказательство. Очевидно, что для указанной функции будем иметь и Но тогда… Теорема доказана.Где величина представляет собой общее решение соответствующего однородного уравнения (2), а величина - суть некоторое частное решение неоднородного уравнения (1).