рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Розв’язання типового варіанта
Реферат Курсовая Конспект
Розв’язання типового варіанта
Розв’язання типового варіанта - раздел Математика, Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика 1. Задано Трикутник З Координатами Вершин А(–2; 4); ...
1. Задано трикутник з координатами вершин А(–2; 4); В(6; –2); С(8; 7). Необхідно знайти: 1) довжину сторони АВ; 2) рівняння сторін АВ і АС та їх кутові коефіцієнти; 3) рівняння медіан, що проведені з вершин А і В, координати центру ваги трикутника; 4) величину кута А в радіанах з точністю до двох знаків; 5) рівняння висоти СТ, проведеної з вершини С на сторону АВ; 6) координати точки М, розташованої симетрично точці В відносно до прямої СТ; 7) Побудувати трикутник АВС медіани, висоту в системі координат 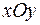 . Зробити малюнок.
. Зробити малюнок.
►1) Відстань між точками A(x1,y1) і B(x2,y2) площини визначається за формулою:
 (11.1)
(11.1)
Застосовуючи (11.1), знаходимо довжину сторони АВ:
 .
.
2) Рівняння прямої, що проходить через точки A(x1, y1) i B(x2, y2), має вигляд
 . (11.2)
. (11.2)
Щоб скласти рівняння сторони АВ, підставляємо в (11.2) координати точок А і В:
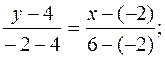
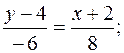
 4y – 16 = –3x – 6;
4y – 16 = –3x – 6;
3x + 4y – 10= 0 (AB).
Для знаходження кутового коефіцієнта прямої АВ (КАВ), розв’я-жемо отримане рівняння відносно у:
4y = –3x + 10; y =  .
.
Отже,
KAB=  .
.
Підставляючи в (11.2) координати точок А і С, здобуваємо рівняння прямої АС:

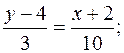
10y – 40 = 3x + 6; 3x – 10y + 46 = 0 (AC),
звідки кутовий коефіцієнт KAC = 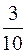 .
.
2. Нехай точка D – середина відрізку ВС, а точка Е – середина
відрізку АС.
Для визначення координат точок D і Е застосовуємо формули:
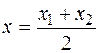 ; y =
; y =  ;
;
xD= 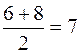 ; yD=
; yD=  , D
, D  ,
,
xE= 
 ; yE=
; yE=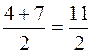 , E
, E 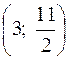 .
.
Підставляючи координати точок А і D в (11.2), маємо рівняння медіани АD:
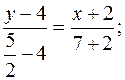
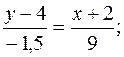

6y – 24 = x – 2; x + 6y – 22 = 0 (AD).
Аналогічно знаходимо рівняння медіани ВЕ:
5x + 2y – 26 = 0 (BE).
Центр ваги трикутника знаходиться в точці N перетину його медіан. Щоб знайти координати цієї точки, необхідно розв’язати систему рівнянь прямих АD і ВЕ.
Унаслідок розв’язку системи
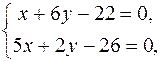
маємо х = 4, у = 3.
Отже, N (4; 3) – точка перетину медіан.
Крім того, відомо, що точка перетину медіан ділить кожну медіану у відношенні 2:1 (починаючи з вершини), тобто
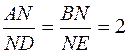 .
.
Тому координати точки N можна знайти також, застосовуючи формули ділення відрізку в даному відношенні:
x=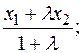
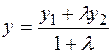 . (11.3)
. (11.3)
Підставляючи в (11.3) координати точок В і Е та вважаючи l=2, маємо:
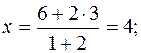
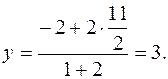
3) Гострий кут між прямими, кутові коефіцієнти яких, відпо-відно, дорівнюють К1 та К2, можна знайти за формулою
 . (11.4)
. (11.4)
Шуканий кут А утворюється прямими АВ і АС, кутові коефі-цієнти яких знайдено раніше. Отже, застосовуючи формулу (11.4), маємо:
tgA=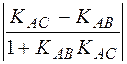 =
=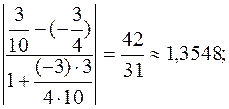
ÐA = arctg 1,3548»53,480.
Скориставшись таблицями переведення градусної міри в радіанну, знаходимо
ÐA » 0,935 рад.
4) Рівняння прямої, що проходить через дану точку в даному напрямку, має вигляд
y – y1=K(x– x1). (11.5)
Для знаходження кутового коефіцієнта висоти СТ скористаємось умовою перпендикулярності прямих СТ і АВ:  = –1. Оскільки
= –1. Оскільки 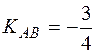 , то
, то 
Підставляючи в (11.5) координати точки С, а також значення знайденого кутового коефіцієнта висоти СТ, маємо:
 ; 3y – 21 = 4x – 32; 4x –3 y – 11 = 0 (CT).
; 3y – 21 = 4x – 32; 4x –3 y – 11 = 0 (CT).
5) Пряма АВ перпендикулярна до прямої СТ, а шукана точка М, симетрична точці В (2; –2) відносно до прямої СТ, належить прямій АВ. Крім того, точка Т є серединою відрізку МВ. Визначимо координати точки Т. Для цього розв’яжемо систему рівнянь, яку утворюють рівняння прямих АВ і СТ.
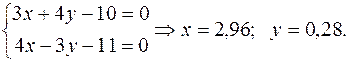
6) Враховуючи, що точка Т (2,96; 0,28) – середина відрізку МВ, а також користуючись формулами (11.3), знайдемо координати точки М:
2,96 = 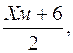 ХM = -0,28;
ХM = -0,28;
0,28 = 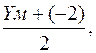 YM = 2,56.
YM = 2,56.
7) Трикутник АВС, медіани АD і ВЕ, точку N їх перетину, висоту СТ, що побудовані в системі координат 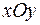 , подано на рис. 1.
, подано на рис. 1.


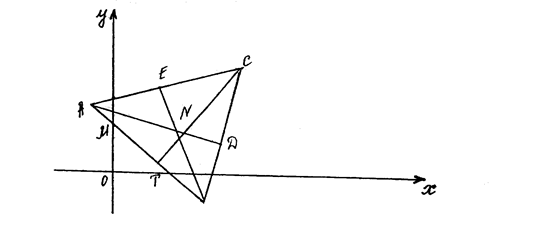
Рис. 1
2. Скласти канонічне рівняння гіперболи, що симетрична відносно до осей координат і проходить через точки А (8; 2 ) і В (–6;
) і В (–6;  ). Знайти півосі, фокуси, ексцентриситети та рівняння асимптоти цієї гіперболи, а також усі точки перетину гіперболи з колом, центр якого знаходиться на початку координат, а радіус R = 6.
). Знайти півосі, фокуси, ексцентриситети та рівняння асимптоти цієї гіперболи, а також усі точки перетину гіперболи з колом, центр якого знаходиться на початку координат, а радіус R = 6.
►Канонічне рівняння шуканої гіперболи має вигляд
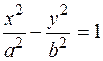 . (11.6)
. (11.6)
За умови задачі точки А і В знаходяться на гіперболі, отже координати цих точок задовольняють рівнянню (11.6). Підставляючи в рівняння (11.6) замість поточних координат Х та У координати даних точок, одержуємо систему двох рівнянь відносно до параметрів a і b.
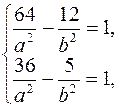 або
або 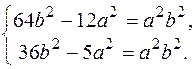
Віднімаючи від першого рівняння друге, маємо 28b2 – 7a2 = 0, звідси a2 = 4b2. Після підставляння у перше рівняння маємо: 64b2 – 48b2 = 4b2b2, b2 = 4, тоді a2 = 16.
Шукане рівняння гіперболи має вигляд:
 (11.7)
(11.7)
Півосі гіперболи а=4; b=2. Визначаємо фокуси гіперболи F1(–C; 0) i F2(C; 0). Користуючись рівністю c2 = a2 + b2, маємо:
c2 =16+4=20, c = 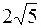 .
.
Отже, F1(2 ,0) та F2(–2
,0) та F2(–2 ,0) – фокуси гіперболи.
,0) – фокуси гіперболи.
Ексцентриситет гіперболи визначаємо за формулою 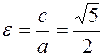 .
.
Рівняння асимптот гіперболи мають вигляд
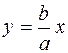 i
i 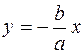 .
.
Отже,  i
i 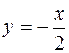 шукані рівняння асимптот. Рівняння кола, центр якого знаходиться на початку координат, має вигляд
шукані рівняння асимптот. Рівняння кола, центр якого знаходиться на початку координат, має вигляд
x2 + y2 = R2.
– Конец работы –
Эта тема принадлежит разделу:
Тематичні індивідуальні завдання та приклади розв’язання типових завдань з курсу „Вища математика
ХАРКІВСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ ХАРЧУВАННЯ... ТА ТОРГІВЛІ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Розв’язання типового варіанта
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов