Формулы и тавтологии логики предикатов.

 

 

При введении определения формул логики предикатов будем использовать следующие обозначения (алфавит):

1) – индивидные переменные,

2) 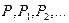– предикатные буквы.

Из предикатных букв, индивидных переменных, символов логических операций и скобок можно составлять различные выражения, некоторые из которых называются формулами.

Определение 1: Формулами исчисления предикатов являются:

а) каждая предикатная буква и каждая предикатная буква со следующими за ней в скобках индивидными переменными (их будем называть предикатными буквами с приданными переменными);

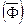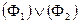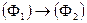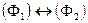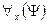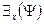б) выражения , , , , , и , где 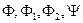– некоторые формулы, – индивидная переменная. Их будем называть соответственно: отрицанием формулы 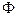, конъюнкцией, дизъюнкцией, импликацией, эквивалентностью формул и квантификацией формулы 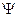по переменной кванторами общности и существования.

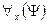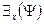В выражениях и формула 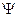называется областью действия квантора. Индивидная переменная, входящая в формулу, называется свободной, если она не следует непосредственно за квантором и не входит в область действия квантора. Все другие переменные, входящие в формулу, называются связными.

Из определения формулы видно, что каждая формула исчисления предикатов является или предикатной буквой с некоторым числом приданных переменных (), или получается из конечной совокупности предикатных букв с приданными переменными последовательным применением п. б) сначала к данным предикатным буквам, затем к формулам, которые из них образованы. Строение формулы определяется расположением скобок.

Из определения следует, что каждая формула исчисления предикатов обратится в некоторый предикат, если входящие в неё предикатные буквы с приданными переменными заменить какими-либо предикатами с соответствующим числом переменных, принимающих значения в некоторых множествах. В частности, формула, все переменные которой связаны, обратится при этом в высказывание.

Формула исчисления предикатов имеет смысл только тогда, когда имеется интерпретация входящих в неё символов. Под интерпретацией мы понимаем всякую систему, состоящую из множества (область интерпретации) и отображения, которое каждой предикатной букве с приданными переменными ставит в соответствие некоторый предикат, определённый на множестве . Предполагается, что каждая предметная переменная пробегает значения всех элементов из множества . Предметная переменная – это фиксированный элемент из множества . Для данной интерпретации всякая формула без свободных переменных (т. е. замкнутая формула) представляет собой высказывание, которое истинно или ложно. А формула, в которую входят свободные переменные, выражает некоторое отношение на области интерпретации; это отношение может быть истинным для одних значений переменных и ложным – для других. Ясно, что всякая формула имеет бесконечное множество интерпретаций.

Определение 2: Формула исчисления предикатов называется тавтологией (или общезначимой формулой), если она принимает значение «истина» при любой интерпретации.

В исчислении высказываний был указан простой общий метод определения, является ли данная формула тавтологией или нет, состоящий в построении таблицы истинности. В исчислении предикатов доказано, что не существует способа, позволяющего выяснить, является ли произвольная формула исчисления предикатов общезначимой. Это - первая алгоритмически неразрешимая проблема, установленная в математике. Для решения этой задачи и была создана теория алгоритмов.

Нахождение тавтологий является одной из основных задач логики предикатов.

Простейшие тавтологии исчисления предикатов можно строить, пользуясь следующей теоремой.

Теорема 1: Формула исчисления предикатов, получающаяся из тавтологии исчисления высказываний при замене входящих в нее пропозиционных букв предикатными буквами с произвольным числом приданных переменных, является тавтологией исчисления предикатов.

Рассмотрим для примера следующую формулу:

.

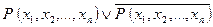Эта формула получена из закона исключенного третьего логики высказываний с помощью замены пропозиционной буквы 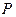на предикатную букву с приданными переменными. Докажем, что данная формула логики предикатов является тавтологией.

Доказательство: Пусть – произвольный - местный предикат, определенный на произвольном множестве . В этой интерпретации получим - местный предикат 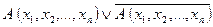путём подстановки его вместо предикатной буквы . Для любого набора значений аргументов предикат или его отрицание принимают значение «истина» (т. к. 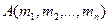- высказывание). Но тогда значение дизъюнкции для этих аргументов будет «истина». Следовательно, делаем вывод, что предикат 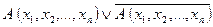тождественно истинный. В силу произвольности выбора предиката можно утверждать о справедливости доказываемого утверждения.

Теорема 2: Следующие формулы исчисления предикатов являются тавтологиями:

1) ,

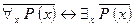2) 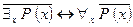- законы де Моргана;

3) ,

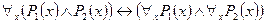4) - законы пронесения квантора общности через конъюнкцию и дизъюнкцию (Р не зависит от );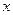

5) ,

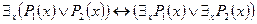6) 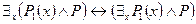- законы пронесения квантора существования через конъюнкцию и дизъюнкцию (Р не зависит от );

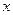7) ,

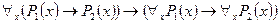8) 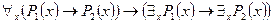- законы пронесения кванторов через импликацию;

9) 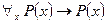- закон удаления квантора общности;

10) 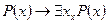- закон введения квантора существования;

11) ,

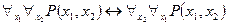12) 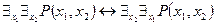- законы коммутативности для кванторов.

Доказательство: Докажем некоторые равносильности.

(1) Для доказательства первого утверждения (закон де Моргана) нужно показать, что всякий раз, когда левая часть равносильности принимает значение «истина», правая часть также принимает значение «истина», и наоборот. Заменим предикатную букву любым предикатом, определённым на множестве (т. е. рассмотрим произвольную интерпретацию). Проверим, что логические значения левой и правой частей эквивалентности совпадают:

а) Пусть 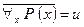, тогда 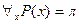. Последнее утверждение справедливо только в том случае, когда 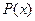не является тождественно истинным предикатом, а значит 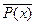- выполнимый предикат. Следовательно, по определению, .

б) Пусть , тогда 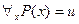. Последнее высказывание может быть истинным только в одном случае, когда 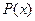тавтология, а значит 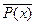- тождественно ложный предикат. Следовательно, по определению, .

(2) Второй закон де Моргана доказывается аналогично.

(3) Докажем закон пронесения квантора общности через конъюнкцию. Заменим все предикатные буквы произвольными предикатами, определёнными на некотором множестве . Покажем, что логические значения левой и правой частей эквивалентности совпадают:

а) пусть левая часть равносильности принимает значение «истина», т. е. 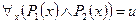, тогда, по определению квантора общности, для любого значения 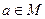: 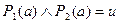. Следовательно, по определению конъюнкци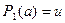и, и 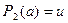. Значит, по определению квантора общности: 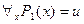, 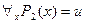. Тогда, по определению конъюнкции, .

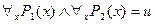б) пусть правая часть формулы принимает значение «истина», значит, 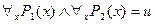, тогда, по определению конъюнкции, имеем 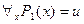и 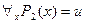. По определению квантора общности, каким бы ни был элемент 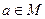, выполняются условия: 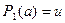и 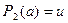. Тогда для каждого элемента 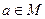: имеем 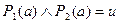. Следовательно, по определению квантора общности: 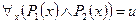. Утверждение доказано.

(4) Высказывание 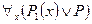будет истинным тогда и только тогда, когда дизъюнкция 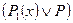- тождественно истинна, т. е. 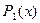- тождественно истинный предикат для любого значения переменной 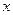, или высказывание 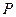истинно. Значит, истинной будет дизъюнкция .

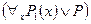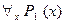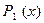(7) Действительно, заключение импликации будет ложным только в том случае, когда универсальное высказывание истинно, а универсальное высказывание ложно, т.е. когда – тождественно истинный предикат, а 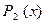– не тождественно истинный предикат. Следовательно, предикат 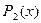не будет следствием предиката 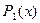, но тогда импликация не является тождественно истинной, и, следовательно, соответствующее универсальное высказывание 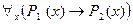ложно. Таким образом, импликация 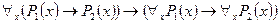не может быть ложной.

(9) Докажем закон удаления квантора общности: 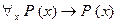. Индивидная переменная , входящая в заключение данной импликации, является свободной переменной. Следовательно, если в этой формуле предикатную букву 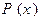заменим каким-либо предикатом , определенным на некотором множестве 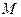, то получим одноместный предикат, определенный на том же множестве 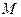: . Покажем, что он является тождественно истинным. Действительно, в противном случае существовал бы аргумент 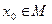, для которого предикат принимал бы значение «ложь». Но это возможно лишь в случае, когда значение предиката в точке есть «ложь», а универсальное высказывание, соответствующее предикату , истинно. Следовательно, предикат , с одной стороны, не тождественно истинный, а с другой стороны – тождественно истинный, что невозможно. Утверждение доказано.

Аналогично можно доказать все остальные утверждения.

Замечание: Из законов де Моргана следует, что каждый из кванторов может быть выражен через двойственный ему квантор и отрицание:

 

Доказанные выше тавтологии можно обобщить.

Теорема 3: Если в тавтологии исчисления предикатов к входящим в нее предикатным буквам приписать любое конечное число свободных индивидных переменных, то полученная формула также будет тавтологией исчисления предикатов.

Докажем, для примера, справедливость утверждения теоремы для закона де Моргана, т.е. докажем, что следующая формула является тавтологией: .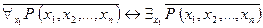

Доказательство. В этой формуле переменная 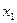– связная, а переменные 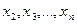– свободные. Следовательно, меняя в формуле предикатную букву на какой-нибудь - местный предикат , определенный на прямом произведении 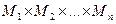, получим - местный предикат, определенный на множестве :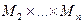

.

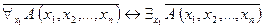Покажем, что полученный предикат является тождественно истинным. Достаточно доказать, что логические значения членов последней эквивалентности для произвольных наборов элементов 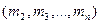из множества 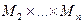соответственно совпадают.

Действительно, рассмотрим одноместный предикат 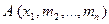, определенный на множестве . Но для предикатов от одной переменной закон де Моргана уже доказан, следовательно будет истинна эквивалентность:

.

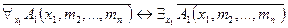Следовательно, логические значения ее членов совпадают. Но логические значения членов эквивалентности 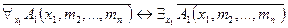совпадают со значениями соответствующих членов эквивалентности 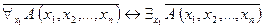для любых наборов 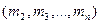. Отсюда, в силу произвольности выбора предиката следует, что формула 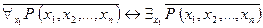является тавтологией. Что и требовалось доказать.