рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Свойства теорий первого порядка.
Реферат Курсовая Конспект
Свойства теорий первого порядка.
Свойства теорий первого порядка. - раздел Математика, КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ Все Результаты Этого Параграфа Относятся К Пр...
Все результаты этого параграфа относятся к произвольной теории  первого порядка. Всякая теория первого порядка является формальной теорией.
первого порядка. Всякая теория первого порядка является формальной теорией.
Определение 1: Формула  называется частным случаем формулы
называется частным случаем формулы  , если формула
, если формула  получается из формулы
получается из формулы  с помощью подстановки некоторой формулы
с помощью подстановки некоторой формулы  вместо всех вхождений некоторой пропозиционной буквы.
вместо всех вхождений некоторой пропозиционной буквы.
Теорема 1: Если формула  некоторой теории
некоторой теории  является частным случаем тавтологии, то формула
является частным случаем тавтологии, то формула  - есть теорема в теории
- есть теорема в теории  и может быть выведена с помощью только схем аксиом (А1) - (А3) и правила modus ponens.
и может быть выведена с помощью только схем аксиом (А1) - (А3) и правила modus ponens.
Доказательство: Пусть формула  получена из некоторой тавтологии
получена из некоторой тавтологии  с помощью подстановок. Тогда существует вывод формулы
с помощью подстановок. Тогда существует вывод формулы  в теории
в теории  (т. к. всякая тавтология в теории
(т. к. всякая тавтология в теории  является теоремой). Сделаем теперь всюду в этом выводе подстановки по следующему правилу:
является теоремой). Сделаем теперь всюду в этом выводе подстановки по следующему правилу:
1) если какая-нибудь пропозиционная буква входит в  , то на месте всех её вхождений в каждую формулу вывода подставляем ту формулу теории
, то на месте всех её вхождений в каждую формулу вывода подставляем ту формулу теории  , которая подставлялась в тавтологию
, которая подставлялась в тавтологию  на места вхождений той же буквы при построении формулы
на места вхождений той же буквы при построении формулы  ;
;
2) если данная пропозиционная переменная не входит в формулу  , то на места всех её вхождений в формулы вывода подставляем произвольную (одну и ту же для данной буквы) формулу теории
, то на места всех её вхождений в формулы вывода подставляем произвольную (одну и ту же для данной буквы) формулу теории  .
.
Полученная таким образом последовательность формул будет выводом формулы  в теории
в теории  . Теорема доказана.
. Теорема доказана.
Если теория первого порядка не содержит собственных аксиом, то она называется исчислением предикатов первого порядка.
Теорема 2: Всякое исчисление предикатов  первого порядка непротиворечиво.
первого порядка непротиворечиво.
Доказательство: Для произвольной формулы  обозначим через
обозначим через 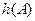 выражение, которое получается в результате следующего преобразования формулы
выражение, которое получается в результате следующего преобразования формулы  : в этой формуле опускаются все кванторы и термы (вместе с соответствующими скобками и запятыми).
: в этой формуле опускаются все кванторы и термы (вместе с соответствующими скобками и запятыми).
Например, 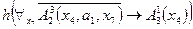 есть
есть  .
.
По существу, 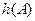 всегда является формулой алгебры высказываний, в которой роль пропозиционных букв играют предикатные буквы
всегда является формулой алгебры высказываний, в которой роль пропозиционных букв играют предикатные буквы 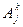 .
.
Очевидно, что 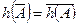 и
и  . Для всякой аксиомы
. Для всякой аксиомы  , полученной по схеме аксиом (1)-(5), выражение
, полученной по схеме аксиом (1)-(5), выражение 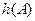 является тавтологией. Это очевидно для схем аксиом (А1) - (А3). Всякий частный случай
является тавтологией. Это очевидно для схем аксиом (А1) - (А3). Всякий частный случай  схемы (4) преобразуется операцией
схемы (4) преобразуется операцией  в тавтологию вида
в тавтологию вида 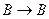 , а всякий частный случай
, а всякий частный случай  схемы (А5) преобразуется в тавтологию вида
схемы (А5) преобразуется в тавтологию вида  .
.
Наконец, если 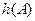 и
и  тавтологии, то и
тавтологии, то и 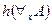 - есть тавтология, т. к. результаты применения операции
- есть тавтология, т. к. результаты применения операции  к формуле
к формуле  и
и  совпадают. Следовательно, если
совпадают. Следовательно, если  есть теорема в теории
есть теорема в теории  , то
, то 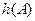 есть тавтология.
есть тавтология.
Если бы существовала формула  в теории
в теории  , такая, что ├К
, такая, что ├К и ├К
и ├К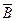 (здесь знаком ├К обозначается вывод в теории
(здесь знаком ├К обозначается вывод в теории  ), то оба выражения
), то оба выражения  и
и 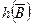 были бы тавтологиями, что невозможно. Таким образом, теория
были бы тавтологиями, что невозможно. Таким образом, теория  непротиворечива. Что и требовалось доказать.
непротиворечива. Что и требовалось доказать.
Замечание: Операция  равносильна интерпретации
равносильна интерпретации  в области, состоящей из одного элемента. Все теоремы теории
в области, состоящей из одного элемента. Все теоремы теории  истинны в такой интерпретации, однако ни в какой интерпретации никакая формула не может быть истинной вместе со своим отрицанием.
истинны в такой интерпретации, однако ни в какой интерпретации никакая формула не может быть истинной вместе со своим отрицанием.
Теорема дедукции для исчисления высказываний без соответствующей модификации не может быть проведена для произвольных теорий  первого порядка.
первого порядка.
Например,  ├К
├К для любой формулы
для любой формулы  , но далеко не всегда справедлив вывод ├К
, но далеко не всегда справедлив вывод ├К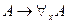 . В самом деле, рассмотрим область, содержащую по крайней мере два элемента
. В самом деле, рассмотрим область, содержащую по крайней мере два элемента 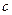 и
и 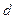 . Пусть
. Пусть  - есть некоторое исчисление предикатов. Пусть
- есть некоторое исчисление предикатов. Пусть  есть
есть  . Проинтерпретируем
. Проинтерпретируем  каким-нибудь свойством, которым обладает только элемент
каким-нибудь свойством, которым обладает только элемент 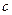 . Тогда
. Тогда  выполнено для значения
выполнено для значения  , но
, но  не выполняется. Следовательно, формула
не выполняется. Следовательно, формула 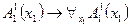 не является истинной в этой интерпретации, и поэтому не является логически общезначимой. Далее будет доказано, что всякая теорема всякого исчисления предикатов является логически общезначимой.
не является истинной в этой интерпретации, и поэтому не является логически общезначимой. Далее будет доказано, что всякая теорема всякого исчисления предикатов является логически общезначимой.
Однако, некоторая «ослабленная», но полезная форма теоремы дедукции и здесь может быть доказана.
Пусть  - некоторая формула, принадлежащая заданному множеству формул
- некоторая формула, принадлежащая заданному множеству формул  , и пусть
, и пусть 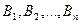 - какой-нибудь вывод из
- какой-нибудь вывод из  , снабженный обоснованием каждого шага. Мы будем говорить, что формула
, снабженный обоснованием каждого шага. Мы будем говорить, что формула 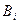 зависит от
зависит от  в этом выводе, если:
в этом выводе, если:
1) 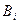 есть
есть  и обоснованием
и обоснованием 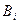 есть принадлежность
есть принадлежность 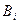 к множеству
к множеству  , или
, или
2) 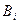 обосновано, как непосредственное следствие по правилу modus ponens или по правилу обобщения (
обосновано, как непосредственное следствие по правилу modus ponens или по правилу обобщения ( ) некоторых предшествующих в этом выводе формул, из которых, по крайней мере, одна зависит от формулы
) некоторых предшествующих в этом выводе формул, из которых, по крайней мере, одна зависит от формулы  .
.
Например, 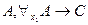 ├
├ .
.
(В1)  - гипотеза.
- гипотеза.
(В2)  - выводится из (В1) по правилу
- выводится из (В1) по правилу  .
.
(В3)  - гипотеза.
- гипотеза.
(В4)  - выводится из (В2), (В3) по правилу
- выводится из (В2), (В3) по правилу  .
.
(В5)  - получается из (В4) по правилу
- получается из (В4) по правилу  .
.
Здесь (В1) зависит от  , (В2) зависит от
, (В2) зависит от  , (В3) зависит от
, (В3) зависит от  , (В4) зависит от
, (В4) зависит от  и от
и от  , (В5) зависит от
, (В5) зависит от  и от
и от  .
.
Теорема 3: Если  не зависит от
не зависит от  в выводе
в выводе 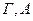 ├
├ , то
, то  ├
├ .
.
Доказательство: Пусть  вывод
вывод  из
из  и
и  , в котором
, в котором  не зависит от
не зависит от  . Докажем теорему индукцией по числу
. Докажем теорему индукцией по числу  . При
. При 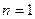 утверждение теоремы очевидно. Предположим, что утверждение теоремы справедливо для таких выводов, длина которых меньше
утверждение теоремы очевидно. Предположим, что утверждение теоремы справедливо для таких выводов, длина которых меньше  (индуктивное допущение). Если
(индуктивное допущение). Если  принадлежит множеству
принадлежит множеству  или является аксиомой, то
или является аксиомой, то  ├
├ . Если
. Если  является непосредственным следствием некоторых (одной или двух) предшествующих формул, то, поскольку
является непосредственным следствием некоторых (одной или двух) предшествующих формул, то, поскольку  не зависит от
не зависит от  , то от
, то от  не зависит ни одна из данных формул. Следовательно, по индуктивному допущению, из
не зависит ни одна из данных формул. Следовательно, по индуктивному допущению, из  выводимы эти (одна или две) формулы, а вместе с ними и
выводимы эти (одна или две) формулы, а вместе с ними и  . Что и требовалось доказать.
. Что и требовалось доказать.
Теорема 4: (теорема дедукции в теории  ).
).
Пусть 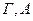 ├
├ и пусть при этом существует такой вывод формулы
и пусть при этом существует такой вывод формулы  из множества
из множества  , в котором ни при каком применении правила обобщения к формулам, зависящим в этом выводе от
, в котором ни при каком применении правила обобщения к формулам, зависящим в этом выводе от  , не связывается квантором никакая переменная формулы
, не связывается квантором никакая переменная формулы  . Тогда
. Тогда  ├
├ .
.
Доказательство: Пусть  - удовлетворяющий условиям теоремы вывод
- удовлетворяющий условиям теоремы вывод  из
из  . Докажем, что
. Докажем, что  ├
├ для любого
для любого  индукцией.
индукцией.
Если 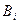 принадлежит множеству
принадлежит множеству  или является аксиомой, то
или является аксиомой, то  ├
├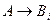 , т. к.
, т. к. 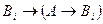 - аксиома. Если
- аксиома. Если 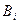 совпадает с
совпадает с  , то
, то  ├
├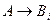 , т. к. ├
, т. к. ├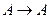 теорема 1. Если существуют
теорема 1. Если существуют 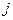 и
и 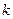 , меньшие
, меньшие 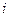 , такие что
, такие что 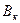 есть
есть 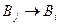 , то
, то  ├
├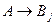 и
и  ├
├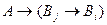 (по индуктивному предположению). Следовательно, по схеме аксиом (А2) и правилу
(по индуктивному предположению). Следовательно, по схеме аксиом (А2) и правилу  имеем:
имеем:  ├
├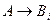 .
.
Предположим, наконец, что существует  такое, что
такое, что 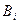 есть
есть  . По предположению:
. По предположению:  ├
├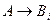 . Здесь либо
. Здесь либо  не зависит от
не зависит от  , либо переменная
, либо переменная  не является свободной в формуле
не является свободной в формуле  . Если
. Если  не зависит от
не зависит от  , то в силу теоремы 3 имеем:
, то в силу теоремы 3 имеем:  ├
├ . Тогда, применяя правило
. Тогда, применяя правило  , получаем:
, получаем:  ├
├ , т. е.
, т. е.  ├
├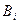 . По схеме аксиом (А1): ├
. По схеме аксиом (А1): ├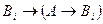 . Отсюда по правилу
. Отсюда по правилу  получаем:
получаем:  ├
├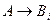 . Если же
. Если же  не является свободной в формуле
не является свободной в формуле  , то по схеме аксиом (А5) имеем:
, то по схеме аксиом (А5) имеем:  ├
├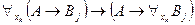 . Так как
. Так как  ├
├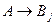 , тогда по правилу
, тогда по правилу  , получаем:
, получаем:  ├
├ . И, наконец, по правилу
. И, наконец, по правилу  имеем:
имеем:  ├
├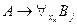 , т. е.
, т. е.  ├
├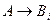 . На этом завершается индукция. Получаем требуемое предложение при условии
. На этом завершается индукция. Получаем требуемое предложение при условии 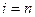 .
.
Условия теоремы 4 громоздки, поэтому иногда удобнее использовать более «слабые» следствия из последней теоремы.
Следствие 1: Если 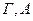 ├
├ и существует вывод, построенный без применения правила обобщения к свободным переменным формулы
и существует вывод, построенный без применения правила обобщения к свободным переменным формулы  , то
, то  ├
├ .
.
Следствие 2: Если формула  замкнута и
замкнута и 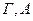 ├
├ , то
, то  ├
├ .
.
Замечание: Из доказательств теорем 3 и 4, следствий из теоремы 4 вытекает, что при построении нового вывода  ├
├ (в случае теоремы 3:
(в случае теоремы 3:  ├
├ ) применение правила
) применение правила  к любой формуле, зависящей от некоторой формулы
к любой формуле, зависящей от некоторой формулы  из множества
из множества  , требуется только в том случае, когда и в данном выводе, т. е. в выводе
, требуется только в том случае, когда и в данном выводе, т. е. в выводе  из
из  , имеется применение правила
, имеется применение правила  (с той же связываемой переменной) к некоторой формуле, зависящей от
(с той же связываемой переменной) к некоторой формуле, зависящей от  .
.
Видно, что  в доказательстве теоремы 4 зависит от той или иной посылки
в доказательстве теоремы 4 зависит от той или иной посылки  из множества
из множества  в первоначальном выводе тогда и только тогда, когда
в первоначальном выводе тогда и только тогда, когда  зависит от
зависит от  в новом выводе.
в новом выводе.
Это замечание может быть полезным, когда нужно применить теорему дедукции несколько раз подряд в процессе доказательства какого-либо утверждения о выводимости. Например, чтобы получить  ├
├ из
из  ├
├ . Поэтому в дальнейшем можно пользоваться этим замечанием наряду с теоремами 3 и 4 и следствиями 1 и 2.
. Поэтому в дальнейшем можно пользоваться этим замечанием наряду с теоремами 3 и 4 и следствиями 1 и 2.
Например, ├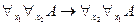 .
.
Доказательство:
1) 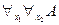 - гипотеза;
- гипотеза;
2)  - схема аксиом (А4);
- схема аксиом (А4);
3) 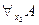 - выводимо из пунктов 1 и 2 по правилу
- выводимо из пунктов 1 и 2 по правилу  ;
;
4) 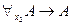 - схема аксиом (А4);
- схема аксиом (А4);
5)  - выводимо из пунктов 3 и 4 по правилу
- выводимо из пунктов 3 и 4 по правилу  ;
;
6)  - выводимо из пункта 5 по правилу
- выводимо из пункта 5 по правилу  ;
;
7) 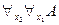 - получается из пункта 6 по правилу
- получается из пункта 6 по правилу  .
.
Таким образом, мы имеем: 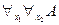 ├
├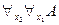 . Причём в построенном выводе, ни при каком применении правила
. Причём в построенном выводе, ни при каком применении правила  не связывается переменная формулы
не связывается переменная формулы 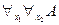 . Поэтому, на основании следствия 2: ├
. Поэтому, на основании следствия 2: ├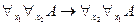 .
.
– Конец работы –
Эта тема принадлежит разделу:
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ... ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ... имени ВЛАДИМИРА ДАЛЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Свойства теорий первого порядка.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов