рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Определение 4: Всякий терм, не содержащий переменных, называется замкнутым термом.
Реферат Курсовая Конспект
Определение 4: Всякий терм, не содержащий переменных, называется замкнутым термом.
Определение 4: Всякий терм, не содержащий переменных, называется замкнутым термом. - раздел Математика, КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ Счётная Интерпретация ...
Счётная интерпретация  теории
теории 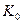 будет иметь своей областью множество замкнутых термов теории
будет иметь своей областью множество замкнутых термов теории 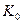 . Согласно лемме 3, это множество является счётным. Если
. Согласно лемме 3, это множество является счётным. Если 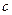 есть предметная константа в теории
есть предметная константа в теории 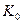 , то она сама и будет своей интерпретацией. Функциональная буква
, то она сама и будет своей интерпретацией. Функциональная буква 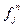 теории
теории 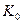 будет интерпретироваться операцией
будет интерпретироваться операцией 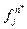 в
в  , имеющей своими аргументами замкнутые термы
, имеющей своими аргументами замкнутые термы  теории
теории 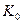 , а значением – замкнутый терм
, а значением – замкнутый терм  той же теории. Отношение
той же теории. Отношение  , интерпретирующее предикатную букву
, интерпретирующее предикатную букву 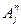 теории
теории 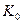 , будет считаться выполненным в
, будет считаться выполненным в  для аргументов
для аргументов  тогда и только тогда, когда ├
тогда и только тогда, когда ├
 . Чтобы доказать, что
. Чтобы доказать, что  является моделью
является моделью 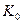 достаточно показать, что произвольная замкнутая формула
достаточно показать, что произвольная замкнутая формула  теории
теории 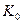 истинна в
истинна в  тогда и только тогда, когда ├
тогда и только тогда, когда ├
 , так как все теоремы теории
, так как все теоремы теории 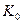 являются также теоремами и теории
являются также теоремами и теории  .
.
Мы докажем это индукцией по числу логических операций и кванторов в формуле  . Пусть сначала
. Пусть сначала  - есть замкнутая элементарная формула. В этом случае, по определению, формула
- есть замкнутая элементарная формула. В этом случае, по определению, формула  истинна в
истинна в  тогда и только тогда, когда ├
тогда и только тогда, когда ├
 . Допустим теперь, что всяка замкнутая формула
. Допустим теперь, что всяка замкнутая формула  с числом операций и кванторов меньшим, чем в формуле
с числом операций и кванторов меньшим, чем в формуле  , истинна в
, истинна в  тогда и только тогда, когда ├
тогда и только тогда, когда ├
 .
.
Случай 1: Формула  имеет вид
имеет вид 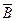 . Если формула
. Если формула  истинна в
истинна в  , то формула
, то формула  ложна в
ложна в  и, следовательно, в силу индуктивного предположения, неверно, что ├
и, следовательно, в силу индуктивного предположения, неверно, что ├
 . Так как теория
. Так как теория  полна, а формула
полна, а формула  замкнута, то ├
замкнута, то ├
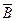 , т. е. ├
, т. е. ├
 . С другой стороны, если
. С другой стороны, если  - ложна в
- ложна в  , то формула
, то формула  истинна в
истинна в  , и тогда ├
, и тогда ├
 . А так как
. А так как  непротиворечива, то неверно, что ├
непротиворечива, то неверно, что ├
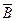 , т. е. ├
, т. е. ├
 .
.
Случай 2: Формула  имеет вид импликации
имеет вид импликации  . Из замкнутости
. Из замкнутости  вытекает замкнутость
вытекает замкнутость  и
и  . Если формула
. Если формула  ложна в
ложна в  , то
, то 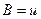 и
и 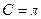 . А силу полноты
. А силу полноты  имеем: ├
имеем: ├
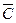 . Тогда из тавтологии
. Тогда из тавтологии 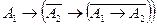 имеем: ├
имеем: ├
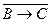 , т. е. ├
, т. е. ├
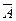 . В силу непротиворечивости
. В силу непротиворечивости  : не ├
: не ├
 . С другой стороны, если неверно, что ├
. С другой стороны, если неверно, что ├
 , то, в силу полноты
, то, в силу полноты  , получим: ├
, получим: ├
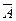 . Принимая во внимание тавтологии
. Принимая во внимание тавтологии 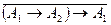 и
и  , получаем: ├
, получаем: ├
 и ├
и ├
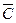 . Следовательно, формула
. Следовательно, формула  истинна в
истинна в  . В силу непротиворечивости
. В силу непротиворечивости  , имеем: не ├
, имеем: не ├
 . Значит, формула
. Значит, формула  ложна в
ложна в  . Таким образом,
. Таким образом,  ложна в
ложна в  .
.
Случай 3: Формула  есть
есть 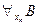 . Тогда при некотором значении
. Тогда при некотором значении 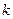 формула
формула  есть
есть  , а
, а 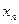 - есть
- есть 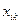 . Здесь есть ещё возможность того, что
. Здесь есть ещё возможность того, что  замкнута и не содержит
замкнута и не содержит 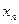 свободно. Но в таком случае формула
свободно. Но в таком случае формула  истинна тогда и только тогда, когда
истинна тогда и только тогда, когда  истинна. Формула
истинна. Формула  будет истинной в данной интерпретации только в том случае, когда в этой интерпретации истинна формула
будет истинной в данной интерпретации только в том случае, когда в этой интерпретации истинна формула 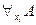 . Поэтому ├
. Поэтому ├
 тогда и только тогда, когда ├
тогда и только тогда, когда ├
 . Таким образом, интересующее нас утверждение для
. Таким образом, интересующее нас утверждение для  следует из соответствующего утверждения для
следует из соответствующего утверждения для  .
.
Предположим, что формула  истинна в
истинна в  , но не ├
, но не ├
 . В силу полноты теории
. В силу полноты теории  имеем: ├
имеем: ├
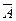 , т. е. ├
, т. е. ├
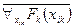 . Однако, известно, что ├
. Однако, известно, что ├
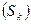 . Следовательно, ├
. Следовательно, ├
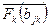 . Так как формула
. Так как формула 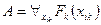 истинна в
истинна в  , то истинной в
, то истинной в  будет также формула
будет также формула 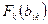 .По индуктивному допущению, получаем: ├
.По индуктивному допущению, получаем: ├
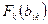 . Таким образом, получили противоречие с фактом непротиворечивости теории
. Таким образом, получили противоречие с фактом непротиворечивости теории  .
.
Допустим теперь, что  - ложна в
- ложна в  , но ├
, но ├
 . Из ложности формулы
. Из ложности формулы 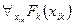 в
в  и из определения
и из определения  , как множества всех замкнутых термов
, как множества всех замкнутых термов 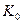 вытекает, что для некоторого замкнутого терма
вытекает, что для некоторого замкнутого терма 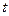 теории
теории 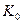 значение
значение 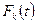 будет ложным. Однако, по предположению, имеем: ├
будет ложным. Однако, по предположению, имеем: ├
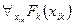 . Следовательно, по аксиоме 4: ├
. Следовательно, по аксиоме 4: ├
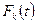 . Далее по индуктивному допущению: формула
. Далее по индуктивному допущению: формула 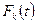 истинна в
истинна в  . Снова пришли к противоречию.
. Снова пришли к противоречию.
Итак,  является счётной моделью для теории
является счётной моделью для теории  , а, следовательно, и для теории
, а, следовательно, и для теории 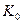 . Так как всякая теорема теории
. Так как всякая теорема теории  является также теоремой теории
является также теоремой теории 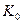 , то множество
, то множество  служит моделью и для теории
служит моделью и для теории  . Теорема доказана полностью.
. Теорема доказана полностью.
Следствие 1: Всякая логически общезначимая формула теории  первого порядка является теоремой теории
первого порядка является теоремой теории  .
.
Доказательство: Достаточно рассмотреть лишь замкнутые формулы  , поскольку всякая формула
, поскольку всякая формула  логически общезначима тогда и только тогда, когда логически общезначимой будет её замыкание, и выводима в теории
логически общезначима тогда и только тогда, когда логически общезначимой будет её замыкание, и выводима в теории  тогда и только тогда, когда в
тогда и только тогда, когда в  выводимо её замыкание.
выводимо её замыкание.
Пусть  - логически общезначимая замкнутая формула теории
- логически общезначимая замкнутая формула теории  . допустим, что
. допустим, что  не является теоремой в
не является теоремой в  . Тогда, если добавить к теории
. Тогда, если добавить к теории  формулу
формулу 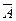 в качестве новой аксиомы, то получим новую теорию
в качестве новой аксиомы, то получим новую теорию 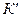 , которая будет непротиворечивой (по лемме 2). Теория
, которая будет непротиворечивой (по лемме 2). Теория 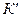 имеет (согласно теореме 2) модель
имеет (согласно теореме 2) модель  . Так как формула
. Так как формула 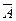 является аксиомой в
является аксиомой в 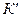 , то
, то 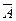 истинна в
истинна в  . А так как формула
. А так как формула  - логически общезначима, то она истинна в
- логически общезначима, то она истинна в  . Получили противоречие: формула
. Получили противоречие: формула  одновременно истинна и ложна в
одновременно истинна и ложна в  , чего быть не может. Противоречие возникло из-за неверного допущения. Значит, формула
, чего быть не может. Противоречие возникло из-за неверного допущения. Значит, формула  должна быть теоремой теории
должна быть теоремой теории  . Что и требовалось доказать.
. Что и требовалось доказать.
Следствие 2: (теорема Геделя (1930) о полноте).
Во всяком исчислении предикатов первого порядка теоремами являются все те, и только те формулы, которые логически общезначимы.
Доказательство: Доказательство этого утверждения следует из теоремы 1 и следствия 2 из теоремы 2, хотя первоначальное доказательство самого Геделя было получено другим путём.
Следствие 3: a) Формула  истинна в каждой счётной модели теории
истинна в каждой счётной модели теории  тогда и только тогда, когда ├К
тогда и только тогда, когда ├К . Следовательно,
. Следовательно,  истинна в каждой модели теории
истинна в каждой модели теории  тогда и только тогда, когда ├К
тогда и только тогда, когда ├К .
.
b) Если во всякой модели теории  формула
формула  выполнена при условии выполнения всех формул некоторого множества формул
выполнена при условии выполнения всех формул некоторого множества формул  , тогда
, тогда  ├К
├К .
.
c) Если формула  теории
теории  является логическим следствием данного множества формул
является логическим следствием данного множества формул  теории
теории  , то
, то  ├К
├К .
.
d) Если формула  теории
теории  является логическим следствием формулы
является логическим следствием формулы  из этой же теории, то
из этой же теории, то  ├К
├К .
.
Доказательство: a) Можно считать, что формула  замкнута. Допустим, что формула
замкнута. Допустим, что формула  истинна в любой счётной модели теории
истинна в любой счётной модели теории  . Если не ├К
. Если не ├К , то теория
, то теория  непротиворечива. Следовательно, теория
непротиворечива. Следовательно, теория 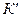 имеет счётную модель
имеет счётную модель 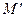 . Формула
. Формула 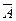 , как аксиома теории
, как аксиома теории 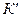 , является истинной в
, является истинной в  . Но
. Но  является также моделью и для теории
является также моделью и для теории  , поэтому формула
, поэтому формула  истинна в
истинна в 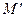 . Таким образом, формула
. Таким образом, формула  одновременно истинна и ложна в
одновременно истинна и ложна в  . Получили противоречие, которое возникло из-за неверного допущения. Требуемое утверждение доказано.
. Получили противоречие, которое возникло из-за неверного допущения. Требуемое утверждение доказано.
b) Рассмотрим теорию 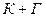 .Формула
.Формула  истинна в каждой модели этой теории. Тогда из утверждения (а) имеем: ├К+Г
истинна в каждой модели этой теории. Тогда из утверждения (а) имеем: ├К+Г , следовательно,
, следовательно,  ├К
├К .
.
c) Данное утверждение следует из пункта (b).
d) Последнее утверждение является частным случаем пункта (c).
Раньше было доказано, что в формальном исчислении высказываний (теория 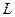 ) произвольная формула является тавтологией тогда и только тогда, когда эта формула является теоремой теории
) произвольная формула является тавтологией тогда и только тогда, когда эта формула является теоремой теории 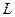 . Следствия 1-3 показывают, что и для логики предикатов справедливы соответствующие утверждения.
. Следствия 1-3 показывают, что и для логики предикатов справедливы соответствующие утверждения.
Следствие 4: Если теория первого порядка  имеет какую-нибудь модель, то она имеет и счётную модель.
имеет какую-нибудь модель, то она имеет и счётную модель.
Доказательство: Если  имеет модель, то теория
имеет модель, то теория  - непротиворечива. Следовательно, по теореме 2,
- непротиворечива. Следовательно, по теореме 2,  имеет счётную модель. Что и требовалось доказать.
имеет счётную модель. Что и требовалось доказать.
Замечание: Можно доказать, что для любого кардинального числа  всякая непротиворечивая теория имеет модель мощности
всякая непротиворечивая теория имеет модель мощности  .
.
Правило индивидуализации: Если терм 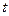 свободен для переменной
свободен для переменной 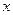 в формуле
в формуле  , то
, то 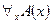 ├
├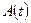 .
.
Доказательство: Из формулы 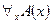 и схемы аксиом (А4) имеем:
и схемы аксиом (А4) имеем:  , по правилу
, по правилу  получаем
получаем 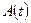 . Верно и обратное. Не сложно доказать, что формула
. Верно и обратное. Не сложно доказать, что формула  - общезначима, а значит является теоремой, т. е.
- общезначима, а значит является теоремой, т. е.  .
.
Не сложно также доказать следующие формулы: 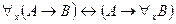 ,
, 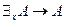 ,
, 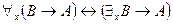 .
.
В качестве примера приведём доказательство следующей формулы:
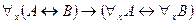 .
.
Доказательство:
1) 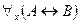 - гипотеза;
- гипотеза;
2)  - гипотеза;
- гипотеза;
3)  - выводится из пункта 1 по правилу индивидуализации;
- выводится из пункта 1 по правилу индивидуализации;
4)  - выводится из пункта 2 по правилу индивидуализации;
- выводится из пункта 2 по правилу индивидуализации;
5)  - получается из пунктов 3 и 4 с помощью правила
- получается из пунктов 3 и 4 с помощью правила  и тавтологии
и тавтологии 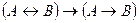 ;
;
6)  - выводится из пункта 5 по правилу
- выводится из пункта 5 по правилу  ;
;
7) 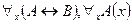 ├
├ - получается из пунктов 1 – 6;
- получается из пунктов 1 – 6;
8) 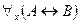 ├
├ - получается из пунктов 1 – 7;
- получается из пунктов 1 – 7;
9) 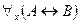 ├
├ - аналогично пункту 8;
- аналогично пункту 8;
10) 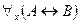 ├
├ - из пунктов 8 и 9;
- из пунктов 8 и 9;
11) ├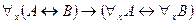 - из пунктов 1 – 10.
- из пунктов 1 – 10.
– Конец работы –
Эта тема принадлежит разделу:
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ... ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ... имени ВЛАДИМИРА ДАЛЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Определение 4: Всякий терм, не содержащий переменных, называется замкнутым термом.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов