рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Отрицание – обозначается ,читается:«не » или «неверно, что ».
Реферат Курсовая Конспект
Отрицание – обозначается ,читается:«не » или «неверно, что ».
Отрицание – обозначается ,читается:«не » или «неверно, что ». - раздел Математика, КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ 2) Дизъюнкция (Логическое Сложение), Обозначаемое...
2) Дизъюнкция (логическое сложение), обозначаемое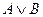 (читается «
(читается « или
или  »).
»).
3) Конъюнкция (логическое умножение), обозначаемое 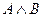 (читается «
(читается « и
и  »).
»).
4) Импликация – обозначается  или
или  (читается «из
(читается «из  следует
следует », «если
», «если  , то
, то  », «
», « влечёт
влечёт  »).
»).
5) Эквивалентность – обозначается  или
или 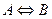 (читается «
(читается « равносильно
равносильно  », «
», « тогда и только тогда, когда
тогда и только тогда, когда  », «для
», «для  необходимо и достаточно
необходимо и достаточно  », «
», « эквивалентно
эквивалентно  »).
»).
6) Сложение по модулю 2 – обозначается  (читается «
(читается « плюс
плюс  »).
»).
Логические операции удобно определять с помощью таблиц истинности. Таблица истинности для отрицания выглядит следующим образом:

| 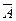
|
| И | Л |
| Л | И |
Отрицание – это одноместная или унарная операция. Отрицание истинного высказывания ложно и наоборот. Так, например, если 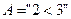 это истинное высказывание, то
это истинное высказывание, то 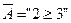 ложно.
ложно.
Остальные логические операции – бинарные или двуместные. Приведём таблицы истинности этих операций:

| 
| 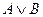
| 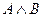
| 
| 
| 
|
| И | И | И | И | И | И | Л |
| И | Л | И | Л | Л | Л | И |
| Л | И | И | Л | И | Л | И |
| Л | Л | Л | Л | И | И | Л |
Из таблицы видно, что дизъюнкцией двух высказываний 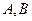 является новое высказывание, обозначаемое
является новое высказывание, обозначаемое 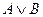 (читается «
(читается « или
или  »), которое считается истинным, если хотя бы одно из высказываний
»), которое считается истинным, если хотя бы одно из высказываний  или
или  истинно, и ложным, если оба они ложны. Следует иметь в виду, что в разговорной речи союз «или» при построении сложных предложений употребляется в двух различных смыслах: не альтернативное (не исключающее) «или» и альтернативное (исключающее) «или». Рассмотрим предложение: «Сегодня вечером мы будем готовиться к математическому анализу или к алгебре». Это предложение утверждает, что вечером мы будем готовиться к одному или к другому предмету, а может быть и к одному, и к другому последовательно (нет альтернативы). А в предложении: «Сегодня вечером мы пойдём на дискотеку или будем заниматься» утверждается, что мы будем либо заниматься, либо развлекаться, исключающее одновременное занятие и тем, и другим. В разных предложениях русского языка союз «или» может также употребляться для противопоставления или для перечисления (в смысле «и»). Кроме того, в русском языке союзом «или» соединяются высказывания, которые как-то связаны по смыслу. В логике дизъюнкция имеет только единственный не альтернативный смысл, зафиксированный в таблице истинности. При этом нас совершенно не интересует смысл высказываний
истинно, и ложным, если оба они ложны. Следует иметь в виду, что в разговорной речи союз «или» при построении сложных предложений употребляется в двух различных смыслах: не альтернативное (не исключающее) «или» и альтернативное (исключающее) «или». Рассмотрим предложение: «Сегодня вечером мы будем готовиться к математическому анализу или к алгебре». Это предложение утверждает, что вечером мы будем готовиться к одному или к другому предмету, а может быть и к одному, и к другому последовательно (нет альтернативы). А в предложении: «Сегодня вечером мы пойдём на дискотеку или будем заниматься» утверждается, что мы будем либо заниматься, либо развлекаться, исключающее одновременное занятие и тем, и другим. В разных предложениях русского языка союз «или» может также употребляться для противопоставления или для перечисления (в смысле «и»). Кроме того, в русском языке союзом «или» соединяются высказывания, которые как-то связаны по смыслу. В логике дизъюнкция имеет только единственный не альтернативный смысл, зафиксированный в таблице истинности. При этом нас совершенно не интересует смысл высказываний 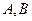 . Важно только истинно или ложно каждое из них.
. Важно только истинно или ложно каждое из них.
Аналогично союз «и» в разных предложениях русского языка может иметь смысл «а», «но», «или». В логике конъюнкция 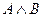 имеет единственный смысл: сложное высказывание «
имеет единственный смысл: сложное высказывание « и
и  » истинно тогда и только тогда, когда каждое из высказываний
» истинно тогда и только тогда, когда каждое из высказываний 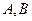 принимает значение «истина».
принимает значение «истина».
Логическая операция, соответствующая обороту «если ..., то ...», посредством которого образуются условные предложения, называется импликацией, обозначается:  . При этом высказывание
. При этом высказывание  называется посылкой (условием) импликации, а
называется посылкой (условием) импликации, а  – заключением (следствием). Импликация ложна только в том случае, когда посылка истинна, а заключение ложно, в остальных случаях импликация считается истинной. В русском языке импликация «из
– заключением (следствием). Импликация ложна только в том случае, когда посылка истинна, а заключение ложно, в остальных случаях импликация считается истинной. В русском языке импликация «из  следует
следует  » употребляется только для высказываний, связанных по смыслу. Например, выражение «Если 2 + 2 = 5, то снег чёрный» в русском зыке не употребляется. Поэтому на первый взгляд может показаться странным, почему высказывания «
» употребляется только для высказываний, связанных по смыслу. Например, выражение «Если 2 + 2 = 5, то снег чёрный» в русском зыке не употребляется. Поэтому на первый взгляд может показаться странным, почему высказывания «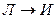 » и «
» и «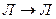 » оба истинны. Однако давно известно, что следствия ложного высказывания могут быть и истинными и ложными. Например, из арифметики известна теорема: «Если натуральное число делится на 4, то оно делится на 2». Применим эту теорему, например, для числа 10. Получим: «Если число 10 делится на 4, то оно делится на 2», т. е. «
» оба истинны. Однако давно известно, что следствия ложного высказывания могут быть и истинными и ложными. Например, из арифметики известна теорема: «Если натуральное число делится на 4, то оно делится на 2». Применим эту теорему, например, для числа 10. Получим: «Если число 10 делится на 4, то оно делится на 2», т. е. «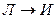 » - верно. Или для числа 11: «Если число 11 делится на 4,то оно делится на 2», т. е. «
» - верно. Или для числа 11: «Если число 11 делится на 4,то оно делится на 2», т. е. «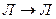 » - истина. Тот факт, что из ложной посылки с помощью «правильных» рассуждений можно получить истинное утверждение, давно известен.
» - истина. Тот факт, что из ложной посылки с помощью «правильных» рассуждений можно получить истинное утверждение, давно известен.
Следующей логической операцией является связка, называемая эквивалентностью. Обозначается:  . Эквивалентность соответствует оборотам типа: «тогда и только тогда, когда ...», «для того, чтобы ..., необходимо и достаточно ...» и т. д. Высказывание
. Эквивалентность соответствует оборотам типа: «тогда и только тогда, когда ...», «для того, чтобы ..., необходимо и достаточно ...» и т. д. Высказывание  принимает значение «истина» тогда и только тогда, когда
принимает значение «истина» тогда и только тогда, когда  и
и  принимают одинаковые истинностные значения. К эквивалентности, как и к предыдущим логическим операциям, относится замечание о том, что её использование в алгебре высказываний никак не учитывает смысловое содержание высказываний
принимают одинаковые истинностные значения. К эквивалентности, как и к предыдущим логическим операциям, относится замечание о том, что её использование в алгебре высказываний никак не учитывает смысловое содержание высказываний  и
и  , к чему мы привыкли в разговорной речи.
, к чему мы привыкли в разговорной речи.
Заметим, что основные логические операции, которые мы определили, не являются независимыми. Нетрудно проверить, что импликация  и дизъюнкция
и дизъюнкция 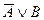 имеют одинаковые таблицы истинности. Аналогично, эквивалентность
имеют одинаковые таблицы истинности. Аналогично, эквивалентность  , конъюнкция
, конъюнкция 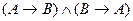 , сложение по модулю 2
, сложение по модулю 2 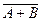 также имеют совпадающие таблицы истинности. Более того, далее будет показано, что всякую логическую операцию можно выразить через дизъюнкцию и отрицание, конъюнкцию и отрицание или через импликацию и отрицание.
также имеют совпадающие таблицы истинности. Более того, далее будет показано, что всякую логическую операцию можно выразить через дизъюнкцию и отрицание, конъюнкцию и отрицание или через импликацию и отрицание.
Введенная нами бинарная операция эквивалентности над высказываниями, рассматриваемая, как бинарное отношение на множестве высказываний, обладает свойствами рефлексивности, симметричности и транзитивности, т.е. является отношением эквивалентности. Соответствующее фактор-множество состоит из классов таких, что если два высказывания принадлежат одному классу, то они эквивалентны. Это множество классов будет булевой алгеброй относительно операций конъюнкции, дизъюнкции и отрицания (также, как и множество всех подмножеств произвольного множества относительно операций объединения, пересечения и дополнения). В полученном множестве классов эквивалентных высказываний роль пустого множества (нуля) играет класс тождественно ложных высказываний, роль универсального множества (единицы) играет класс тождественно истинных высказываний.
– Конец работы –
Эта тема принадлежит разделу:
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ... ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ... имени ВЛАДИМИРА ДАЛЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Отрицание – обозначается ,читается:«не » или «неверно, что ».
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов