Классическое определение вероятности
Тема 1: Формулы комбинаторики и вероятность, аксиомы Колмогорова. Алгебра событий.
Классическое определение вероятности.
Основные понятия.
В жизни часто встречаются ситуации, когда результат проводимого опыта (испытания, наблюдения) нельзя предсказать заранее с полной уверенностью. Так, при бросании монеты нельзя точно сказать, какой стороной она упадет, при покупке лотерейного билета нельзя точно знать, выпадет ли на него выигрыш, при раздаче карт нельзя знать определенно, сколько козырей окажется у вас в руках. Во всех таких случаях результат опыта рассматривают как случайное событие.
Мы будем использовать следующее определение.
Определение 1. Некоторое событие называется случайным по отношению к данному опыту, если оно может как наступить, так и не наступить в результате проведения данного опыта.
Примерами случайных событий являются : присутствие нечетного числа студентов на лекции, выпадение герба при бросании монеты, выигрыш при игре в лотерею, попадание в цель при выстреле и т. д.
Перечисленные выше события могут произойти в опытах, которые можно повторить (в принципе) неограниченное число раз (подсчитать количество студентов на лекции, подбросить монету, купить лотерейный билет, произвести выстрел).
Случайные события, которые могут наступить в таких опытах, называют массовыми.
Примером не массового (единичного) события является такое случайное событие: "15 мая 2002 года в Брянске будет дождь". Это событие не массовое, поскольку данный опыт воспроизвести еще раз невозможно, так как 15 мая 2002 года наступает только один раз.
Предметом теории вероятностей является изучение закономерностей, присущих массовым случайным событиям.
Условимся обозначать случайные события заглавными латинскими буквами. Определение 2. Два случайных события называют несовместными, если наступление… Пример 1. Опыт состоит в бросании игрального кубика. Событие - выпадение четного числа очков. Событие - выпадение 5.…Классическое определение вероятности.
Определение 9. Случайное событие, которое может произойти в результате данного опыта, называется элементарным, если оно не может быть представлено в виде суммы двух несовместных случайных событий. Множество всех элементарных событий для данного опыта называется пространством элементарных событий, которое мы будем обозначать буквой W.
Мы будем рассматривать только такие опыты (испытания), для которых выполняются следующие два условия:
а) Общее число несовместных элементарных событий конечно (то есть множество W -конечно);
б) Осуществление каждого элементарного события равновозможно, то есть условия испытания не создают преимущества в появлении какого-либо элементарного события перед другими.
Пример 8.Опыт состоит в бросании двух игральных кубиков. Элементарное событие состоит в выпадении упорядоченной пары (m, n) на первом и втором кубике соответственно, где m, nÎNи m£6, n£6. Пространство W={(1,1),(1,2),(1,3),¼,(6,6)} состоит из 36 элементарных событий.
Будем обозначать элементарные события w1,w2,¼,wn.Тогда W={w1,w2,¼,wn}.
Замечание 1.Легко видеть, что любое случайное событие A является подмножеством пространства элементарных событий W.
Например, если в опыте из примера 8 рассмотреть событие A, состоящее в том, что сумма выпавших очков не меньше 10, то
A={(5,5), (5,6), (6,5), (6,6),(4,6),(6,4)}. (1)
Определение 10. Говорят, что элементарное событие wkÎW благоприятствует событию A, если наступление события wk влечёт за собой наступление события A (то есть wkÎA).
Например, элементарное событие (5,6) благоприятствует случайному событию A из предыдущего примера.
Замечание 2.Согласно замечанию 1 случайное событие A как подмножество W состоит из случайных элементарных событий, благоприятствующих A .
Определение 11. (Классическое определение вероятности)
ВероятностьюP(A) события A называется отношение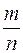 
числа элементарных событий, благоприятствующих событию A, к числу всех элементарных событий, т. е.
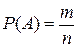. (2)
Замечание 3. Если воспользоваться обозначениями из пункта 2 §2, то
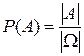. (3)
Напомним, что числа ½A½ и ½W½ есть количество элементов во множествах
A и W соответственно.
При рассмотрении примера 8 мы доказали, что ½W½=36. Из (1) следует, что ½A½=6. Поэтому согласно (3) получим . Пример10. Какова вероятность того, что при двух бросках монеты оба раза может… Иногда предлагается такое решение этой задачи. Так как число гербов может быть равно 0,1 или 2, то общее число…Свойства вероятности.
1) Вероятность любого события A удовлетворяет неравенству: 0£P(A)£1. Действительно, так как AÍW (Замечание 1), то… . 2) Вероятность невозможного события равна 0. Действительно, пусть A- невозможное событие. Тогда ему не…Относительная частота.
Статистическое определение вероятности.
Предположим, что после повторения опыта N раз, событие A произошло M раз. Определение 12. Частотой наступления события A называется выражение .Формулы комбинаторики.
Размещения. Определение 1. Размещением без повторений из n элементов по k называется… Отметим, что из определения сразу следует, что, во-первых, все элементы в размещении без повторений различны (в…Применение формул комбинаторики при решении задач по теории вероятности.
Решение. Пространством элементарных событий в этой задаче будет множество… Пример 2. Найти вероятность того, что при случайном выборе четырёх букв из слова “история” будут получены буквы, из…Общие определения вероятности. Аксиомы А.Н. Колмогорова. Алгебра событий.
В предыдущем параграфе мы рассмотрели классическое определение вероятности для случая, когда пространство элементарных событий конечно. Однако во… Например, пусть опыт состоит в произведении выстрела по круглой мишени . В… Определение вероятности событий в общем случае (для произвольных пространств ) строится аксиоматическим методом.Аксиомы, задающие вероятность.
Определение. Вероятностью называется функция (на ), которая каждому случайному событию ставит в соответствие число и удовлетворяет следующим… Аксиома 1. Аксиома 2.Условная вероятность. Независимые события.
Определение.Вероятностью события при условии, что событие наступило, или просто условной вероятностью события называют выражение (1) Проиллюстрируем это понятие в случае, когда пространство элементарных событий конечно. Пусть , то есть есть число…Формула полной вероятности и Байеса.
Определение. Говорят, что случайные события образуют полную группу событий, если они попарно несовместны (то есть и Такие случайные события называют также гипотезами. Заметим, что для полной группы событий из аксиом 2, 3 следует,…Функция Лапласа и ее свойства.
В этом параграфе мы рассмотрим одну стандартную ситуацию, которая может возникнуть при решении практических задач.
Последовательность независимых испытаний.
Пусть опыт σ повторяется независимо n раз. В каждом испытании событие A может как наступить, так и не наступить. Обозначим через Pn(k)… Теорема(Бернулли).Имеет место формула. . (1)Определение случайной величины.
Случайной величиной называется величина, которая в результате опыта принимает то или иное числовое значение, заранее не известно, какое именно (это… Случайные величины обычно обозначают заглавными латинскими буквами X, Y, Z и… Примерами случайных величин являются:Дискретные случайные величины.
Определение. Случайная величина X называется дискретной, если она принимает конечное или счетное число значений. Пусть X – дискретная случайная величина, принимающая значенияХарактеристики случайных величин.
M[X] = p1x1 + p2x2 + ... + p3x3 + ... (4) Замечание. Математическое ожидание представляет взвешенное среднее значение… В дальнейшем, наряду с обозначением (4), для математического ожидания M[X] будем использовать обозначение .Примеры дискретных случайных величин.
Приведем примеры часто встречающихся случайных величин.
1. Равномерно распределенная случайная величина.
Определение. Случайная величина X называется равномерно распределенной, если она принимает конечное число значений с одинаковой вероятностью, то есть закон распределения имеет вид.
| X | x1 | x2 | ... | xn |
| P | p | p | ... | p |
где pn = 1, то есть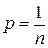 
.
Задача. Доказать, что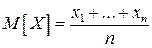 
.
Пример. Бросается игральный кубик. Случайная величина X равна числу выпавших очков. Закон распределения X имеет вид
| X | ||||||
| P |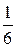 
|
|
|
|
|
|
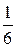
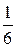
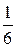
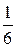
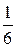
2. Биномиальное распределение.
Производится n независимых опытов. В каждом из них с одной и той же вероятностью p может наступить некоторое событие A. Случайная величина X равна числу наступлений события A в n опытах. Закон распределения случайной величины X имеет вид
| X | ... | k | ... | n – 1 | n | |||
| P | Pn(0) | Pn(1) | Pn(2) | ... | Pn(k) | ... | Pn(n – 1) | Pn(n) |
где по формуле Бернулли
.
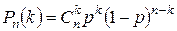Задача.Доказать, что
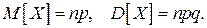
3. Геометрическое распределение.
Рассмотрим схему Бернулли. Пусть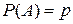 
и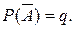 
Случайная величина X равна количеству испытаний до первого наступления события 
.
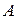Очевидно, что X может принимать любое значение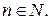 
Легко видеть, что случайная величина X примет значение 
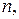если наступит событие 
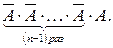Так как все испытания независимы, то
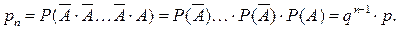
Поэтому закон распределения имеет вид
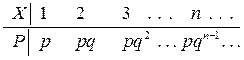
Задача.Доказать, что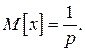 
4. Распределение Пуассона.
Определение.Говорят, что дискретная случайная величина распределена по закону Пуассона, если ее закон распределения имеет вид
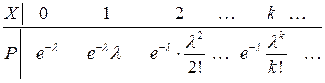
Здесь λ > 0.
Задача.Доказать, что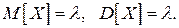 
Тема 6: Функция распределения случайной величины.
Нормально распределенные случайные величины.
Определение. Функцией распределения случайной величины X называется функция , определяемая равенством В дальнейшем будем использовать следующие обозначения:Непрерывная случайная величина.
Утверждение. Если X непрерывная случайная величина, то , то есть вероятность каждого отдельного значения непрерывной случайной величины равна 0. Доказательство. Легко видеть, чтоПримеры непрерывных случайных величин.
Равномерное распределение на отрезке.
где График изображен на рисунке.Среднеквадратичное отклонение.
Математическое ожидание и дисперсия.
плотность вероятности такую, что интегралы и сходятся.Нормированные случайные величины.
Из любой случайной величины с помощью линейного преобразования можно получить нормированную. Теорема. Если X произвольная случайная величина и , то случайная величина -… Доказательство.Определение характеристик случайных величин