Стационарные случайные функции

По определению, случайная функция 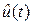является стационарной (в широком смысле), если её математическое ожидание и дисперсия постоянны, а корреляционная функция зависит лишь от расстояния между сечениями случайной функции:

;

;

.

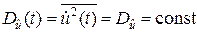Класс стационарных случайных функций достаточно многообразен. Однако в практическом отношении наибольший интерес представляют стационарные случайные функции, обладающие эргодическим свойством, для которых одна реализация достаточно большой продолжительности содержит о случайной функции столько же информации, сколько её содержит и множество реализаций той же суммарной продолжительности. Другими словами, каждая из реализаций эргодической стационарной случайной функции является представителем всего их ансамбля. Как отмечено в работе [12], следует различать эргодические свойства случайных функций по отношению к моментам их распределения различных порядков. При этом под эргодичными обычно понимаются случайные функции, обладающие такими свойствами по отношению к моментам первого и второго порядков, т.е. к математическому ожиданию и корреляционной функции (следовательно, и к дисперсии). Далее рассматриваются только такие случайные функции.

Оценки числовых характеристик эргодичных случайных функций могут быть приближённо определены не как средние по множеству реализаций, а как средние по времени T наблюдения одной реализации по следующим формулам:

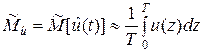, t Î [0; T]; (5.4.6)

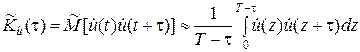, t Î [0; T–t]; (5.4.7)

, t Î [0; T], (5.4.8)

где .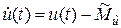

Обоснованием применимости формул (5.4.6) – (5.4.8) служит тот факт, что для эргодичных стационарных случайных функций средние во времени оценки сходятся по вероятности к оцениваемым ими характеристикам , , .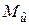

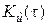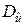Из выражений (5.4.6) – (5.4.8) видно, что для их практического применения требуется интегрировать ряд функций от реализации u(t) случайной функции 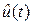. Чаще всего на практике для нахождения оценок (5.4.6) – (5.4.8) используется следующая методика.

Пусть на интервале времени [0; T] наблюдалась реализация эргодичной стационарной случайной функции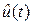, значения которой u(t_j) в ряде равноотстоящих опорных моментов времени t_j = 0,5h + kh, 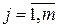, 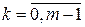зарегистрированы и сведены в табл.5.10.

Таблица 5.10

Значения реализации эргодичной стационарной функции в выбранные моменты времени

t	t1	t2	×××	tj	×××	tm
u(t)	u(t1)	u(t2)	×××	u(tj)	×××	u(tm)

Требуется по данным этой таблицы определить оценки 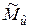, , 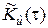числовых характеристик 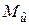, , 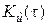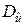случайной функции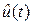

Интервал [0; T] наблюдения случайной функции 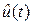разбивается на m равных подынтервалов длиной h = T/m, расположенных симметрично относительно опорных моментов времени t₁, t₂,…, t_m (рис.5.4).

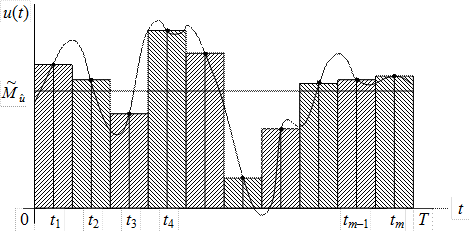
Рис.5.4. Реализация эргодичной стационарной случайной функции

Далее предполагается, что в пределах подынтервала [t_j–0,5h; t_j+0,5h] функция, описывающая реализацию случайной функции, постоянна:

u(t) = u(t_j) = const, t Î [t_j – 0,5h; t_j + 0,5h], ,

Если h достаточно мало, то можно приближённо полагать, что

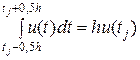, . (5.4.9)

Суммирование результатов (5.4.9) по j даёт

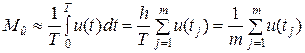. (5.4.10)

Несложно заметить, что выражение (5.4.10) реализует процедуру численного интегрирования по формуле прямоугольников.

Аналогично вычисляется и оценка корреляционной функции для значений аргумента

.

Поскольку в выражении (5.4.7) длина интервала интегрирования

,

то, поделив его на m – l равных участков и вынося на каждом из них за знак интеграла среднее значение функции 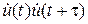, получим

, , (5.4.11)

где L = m/4 [2].

При t = 0 формула (5.4.11) даёт

. (5.4.12)

Вычисления по формуле (5.4.11) ведутся последовательно для l = 0, 1, 2,… вплоть до таких значений l_k, при которых функция 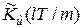становится практически равной нулю или начинает совершать незначительные колебания около нуля. По полученным точкам может быть построен приближённый график корреляционной функции 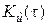(рис.5.5).

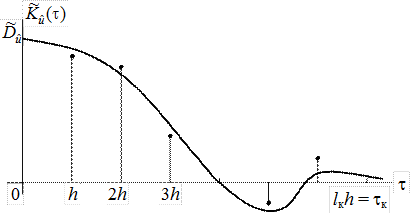
Рис.5.5. Приближённый график корреляционной функции

На представленном рисунке через t_к обозначена длина интервала корреляции случайной функции 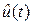, т.е. наименьшее расстояние между сечениями случайной функции, на котором корреляция между ними практически отсутствует (t_к = l_кh).

П р и м е р 5.12. В табл.5.11 приведены результаты наблюдения эргодичной стационарной случайной функции 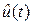на интервале времени продолжительностью T = 28 с с периодичностью h = 1 с в моменты времени t_j, .

Таблица 5.11

Реализация эргодичной стационарной случайной функции

tj, c	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10	t11	t12	t13	t14
u(tj)	4,0	4.1	3,8	2,0	1,0	–0,3	–0,2	1,0	3,5	2,5	2,6	2,0	0,6	2,5
tj, c	t15	t16	t17	t18	t19	t20	t21	t22	t23	t24	t25	t26	t27	t28
u(tj)	3,3	3,8	1,2	0,5	–0,5	0,5	3,2	4,0	2,3	0,5	2,4	3,2	2,0	0,5

Требуется определить оценки числовых характеристик функции .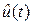

▼ Необходимые вычисления производятся по формулам (5.4.10–(5.4.12). Результаты расчётов оформлены в виде табл.5.12, наглядно иллюстрирующей все этапы решения задачи.

▲

Решение рассмотренной задачи потребовало однократного использования формулы (5.4.10) и одиннадцатикратного – формулы (5.4.11). Если интервал корреляции t_к случайной функции соизмерим с интервалом T её наблюдения, то аргумент t корреляционной функции должен варьироваться от 0 до T. В этом случае параметр l в формуле (5.4.11) пробегает значения от 0 до m –1 и, следовательно, формула (5.4.11) реализуется m раз.

Расчёты показывают, что по сравнению с нестационарными случайными функциями трудоёмкость оценивания числовых характеристик стационарных эргодичных случайных функций существенно снижается.