Представление в виде степенного ряда

Лекция № 1, 2

Представление в виде степенного ряда

F(z)=U(z)+iV(z) Является аналитической в этом круге. Такая функция V называется гармонически… U(z)=ReF(z)

Формула Пуассона

Если R > 1, то мы легко находим, что при r < 1 Суммируя две геометрические прогрессии, получаем

Представление Пуассона для гармонических функций

Представление Пуассона для гармонических функций, принадлежащих некоторым классам

Пусть известно лишь, что функция U(z) гармонична в круге {|z| < 1}. Замечательно, что часто её всё же можно представить в этом круге по формуле Пуассона.

Теорема. Пусть р > 1, и пусть V (г) — гармоническая функция в {z < 1}. Предположим, что средние

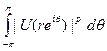
ограничены при r<.1. Тогда существует такая функция 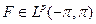, что

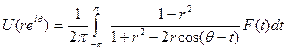
для г < 1,

Доказательство.

При р > 1 пространство является cопряжённым с 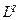, где 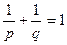. Для функций (вместо подходит любая последова­тельность 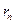, стремящаяся к 1 снизу) имеем (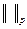здесь, конечно, берётся по отрезку (—π,π)), так что канторовским диагональным процессом мы можем выделить из них подпоследовательность Un_h такую что для всех функ­ций G, пробегающих некоторое счётное всюду плотное подмножество пространства 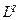, существует предел

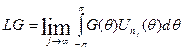
Так как , то этот предел LG на самом деле суще­ствует для всех 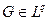и LG является ограниченным линейным функционалом на L^q. Следовательно, поскольку пространство L^p сопряжено с L^q, то существует такая функция , что

всех .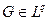

Теперь,для каждого п функция 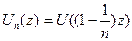гармонична в 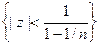, так что если r < 1, то

Зафиксируем произвольное r <. 1 и любое θ и возьмём G (t) = 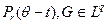. Тогда

В этом равенстве слева стоит

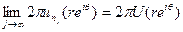
Таким образом,

,

где

Замечание Тот же результат справедлив с тем же дока­зательством и при р =∞, если мы немного изменим форму­лировку теоремы:

Теорема. Если U(z) — ограниченная гармоническая функция в {|z| < 1}, то существует функция 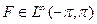, такая что

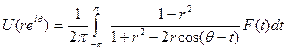
А что же в случае р=1? Пространство , к со­жалению, не является сопряжённым ни с каким другим. Но М — пространство конечных вещественных мер μ на [-π, π] с нормой ||μ||, равной полной вариации меры μ,— сопряжено с С [-π, π] —пространством непрерывных функций на [-π, π]. Если 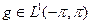то мы можем связать с g меру μ, положив

при этом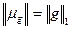

Теперь рассуждение, проведенное при доказательстве пер­вой теоремы этого пункта, показывает, что справедлива такая

Теорема. Если U(z)—гармоническая функция в круге {|z|< 1} и средние

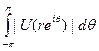
ограничены при r< 1, то существует конечная вещественная мера μ на [-π, π], такая что

для 0≤r< 1.

Следствие (Званс). Пусть U(z)-функция, гармоническая и положительная (здесь и далее «положительный» означает «неотрицательный») в круге {|z|<1}. Тогда существует ко­нечная положительная мера μ на [-π, π],, такая что

Доказательство.

Для r<1 (используя, например, разложение 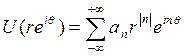, имеющее место в {|z| < 1}) получаем

,

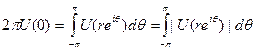гак как 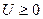. А теперь применяем теорему. Мера μ положи­тельна, потому что в этом случае (см. опять доказательство первой теоремы этого пункта) оказывается, что интеграл 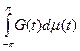положителен для любой положительной функции как предел положительных чисел!

Граничное поведение

Если мы имеем одно из представлений

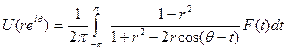
выведенных в предыдущем пункте, то возникает задача на­хождения связи между U(z) и функцией F(t) или мерой dμ(t)

Свойства суммируемости гармонических функций, заданных формулой Пуассона

Ядро Пуассона обладает следующими свойствами:

Первоначальное изучение граничного поведения

Рr(θ)→0 равномерно для σ≤│θ│≤π при r→1. Это сразу следует из формулы для Рr(θ) . Теорема. Пусть функция F непрерывна на R и F(t+2π)=F(θ). Пусть

Лекция 3

Формула Коши-Грина и ее обобщение в случае единичного круга.

Формула Коши

Док-во

Формула Коши-Грина

ς=ξ+iμ z Є inf Г Доказательство окружность

Лекция № 4,5,7

Весовое пространство аналитических в круге функций

Пусть обозначим через – класс всех аналитических в функций , для которых . Если , мы отождествим с классом ограниченных аналитических в круге функций .

Интегральное представление гармонических функций

Пусть – множество всех гармонических в функций; , то есть . В этом параграфе мы построим аналог представления (2.6) для функций из класса . Сначала заметим, что из (2.6)…

Лекция №8

ГАРМОНИЧЕСКИ СОПРЯЖЕННАЯ ФУНКЦИЯ

Формула для гармонически спряженной функции

,   тогда

Лекция 9

Бесконечные числовые произведения комплексных чисел и их сходимость.

(1+а1)(1+а2)(1+а3) .... (1) содержащее бесконечно много сомножителей. Мы обозначаем его через

Логарифм бесконечного произведения.

верно ли, что     Здесь log z главное значение логарифма числа z, т. е. значение, мнимая часть которого…

Лекция 10

Бесконечные функциональные произведения, равномерная сходимость. Бесконечные произведения Бляшке

А. Произведение Бляшке Если .., и бесконечное произведение

Граничные значения почти всюду равны по модулю

Единице

сходится в {|z|< 1} и представляет функцию В(z), аналитическую в этом круге. Согласно элементарной теории функции комплексной переменной, из… Следовательно, для почти всех ζ, |ζ|=1, предельная функция… Теорема.|В(еiθ)|=1 п. в.

Семестр

Лекция 4

Произведение Бляшке. Выделение нулей из класса посредством функции Бляшке.

Возможность построения произведения Бляшке,

имеющего те же нули, что и у заданной функции,

Аналитической в единичном круге

ограничены сверху при r< 1. Тогда

Классы Нр 0 < р < ∞. Факторизация

Определение Если р > 0, то пространство Н^р состоит нз функций F(z) аналитических в {|z|< 1}, для которых

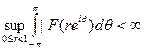(1)

 

Теорема Если 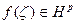р>0, и 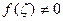, то в ζ|<1 имеем

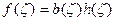(2)

 

где b(ζ)—функция Бляшке, a 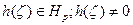в ζ|<1

Доказательство.

Покажем сначала, что интеграл (6.1) есть неубывающая функция от r в 0<r<1. Действительно, при любом фиксированном ρ, 0 <ρ < 1, функция 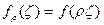регулярна в 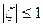и, следовательно, имеет в ζ|<1 представление:

где

b_ρ(ζ)—функция Бляшке, a 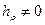в ζ|<1 Функция {h_p(ζ)}^p регулярна в 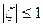; следовательно, из примененной к ней формулы

Пуассона имеем в ζ|<1:

 

Интегрируя это неравенство по Ѳ от 0 до 2π, получаем:

(3)

Но так как 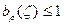в ǀζ|<1 и на ǀζ|=1, то 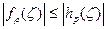в ǀζ|<1 и на ǀζ|=1, следовательно, имеет место неравенство:

доказанное, таким образом, при любых r и ρ из 0<r<1. Заменяя здесь r на ρ'/ρ, ρ'<ρ, и получим неравенство, доказывающее неубывание интеграла (6.1) в 0<r<1.

Обращаясь теперь к доказательству теоремы, отметим, что в ǀζ|<1 имеет место представление (2) с функцией h(ζ), регулярной и без нулей в ǀζ|<1 . Докажем, что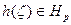

Пусть верхняя граница интегралов (1) в 0<r<1 равна М.

Обозначив через b_n (ζ) произведение n первых множителей в представлении

 

(*)

функции Бляшке b (ζ) и выбирая для заданного ε, 0<ε<1, и фиксированного п такое η>0, чтобы в ǀζ|>1-η было ǀb_n (ζ)ǀ > 1- — s, что возможно, при 1 — η <r < 1 имеем:

(4)

Но так как интеграл в (4) есть неубывающая функция от r 0<r<1, то неравенство (4) имеет место и при 0<r<1—η, т. е. во всем промежутке 0<r<1. Фиксируя r и устремляя n k ∞, из (4) получаем при 0<r<1, учитывая еще произвольность ε>0:

Это и доказывает, что 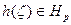и даже более, что верхние границы интегралов (1) для f(ζ) и для h(ζ) в промежутке 0<r<1 будут равны.

Теорема доказана.

 

Следствие. Если 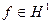, то мы можем найти такие две функции g и h, принадлежащие Н ¹ что и не имеющие нулей в {|z|<1}, что

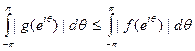
и f=g+h

Замечание. Этот технический результат оказывается часто полезным, так как многие неравенства для функций из Н¹ легче доказывать для функций, не имеющих нулей в {|r|<1}.

Доказательство

Пусть В (r)—произведение Бляшке, построенное по нулям функции f(z). Тогда по предыдущей теореме f= BF, где F(z) не имеет нулей в {|z| < 1}, 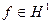и

Мы получаем требуемый., результат, полагая

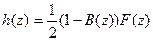
поскольку, как непосредственно проверяется (или же следует из строгого принципа максимума), |В(z)<1 для |z|< 1.

Следствие. Пусть функция , Тогда её можно предста­вить в виде

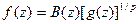
где В (z) — произведение Бляшке, а функция g принадлежит H¹ и не имеет нулей в {|z|<1}.

Доказательство.

Функция f(z) допускает представление f=BF, где функция не имеет нулей в {|z|<1}. Положим g(z) = [F(z)]^p для |z|< 1. Тогда функция g(z) одно­значна н регулярна в круге {|z|<1}, поскольку F нигде нём не обращается в нуль.

Лекция 9 - 12

Приложения неравенства Фейера-Рисса в комплексном анализе. Изучение свойств конформно отображающих функций.

ОБЛАСТИ, ОГРАНИЧЕННЫЕ СПРЯМЛЯЕМОЙ ЖОРДАНОВОИ КРИВОЙ

Пусть Ф— конформное отображение единичного круга на G — область, ограниченную жордановой спрямляемой кривой Г По теореме Каратеодори Ф обладает непрерывным взаимно-однозначным продолжением… 1° Производная конформного отображения принадлежит классу Н1

Образы множеств меры нуль на единичной окружности

Теорема (Ф. и М.. Риссы). Если. j — дуга единичной окружности и = Ф(j),то

Б о

какова бы ни была 2π-периодическая непрерывно дифферен­цируемая функция Т. Пусть теперь 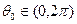, а 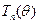— рав­номерно ограниченная последовательность таких функций, сходящаяся к единице в (0,θ₀) и к нулю в [0, 2π] (0,θ₀). Подставляя Т_п вместо Т в последнее равенство и переходя к пределу, по теореме Лебега получаем

Следовательно,

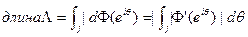
Теорема доказана,

Длина дуги кривой Г может быть очевидным образом использована для определения линейной меры на Г. Сначалапусть Ơ— (относительно) открытое подмножество Г тогда Ơ есть счётное объединение попарно Heпepeceкающихся открытых дуг Ʌ_k, и мы положим |Ơ|=длина Ʌ_k. Для произвольного подмножества 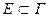определим |E| как inf{|Ơ|: Ơ 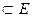, Ơ открыто в Г}. Так как Ф — гомеоморфное отображение окружности {|z|= 1} на Г, то легко показать, основываясь на вышеприведенной теореме, что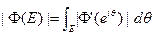

борелевсках множеств Е на единичной окружности. Имеет место следующий важный результат:

Теорема (Ф. и М. Риссы). Если Е - подмножество единичной окружности и {|z|= 1}, то |Ф(Е)| = 0.

Доказательство.

Пусть 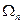— открытые множества на {|z|= 1}, такие что 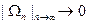Тогда |Ф(Е)|≤|Ф(Ω_п) | для всех n. Но из предыдущей тео­ремы н следующего за ней обсуждения вытекает, что

этот интеграл стремится к нулю при 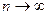так как 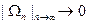и .

Ряд Тэйлора конформного отображении абсолютно сходится вплоть до границы

Дoказательство. По подпункту 1° имеем . Кроме того, поскольку отображение Ф конформно, то…