рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Машиностроение
- /
- Гидросистемы и гидромашины
Реферат Курсовая Конспект
Гидросистемы и гидромашины
Гидросистемы и гидромашины - раздел Машиностроение, Федеральное Агентство По Образованию Государственное Образовательное...
Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
Балтийский государственный технический университет
«Военмех» им. Д.Ф. Устинова
Институт ракетно-космической техники
Факультет авиа- и ракетостроения
Кафедра стартовые и технические комплексы
ракет и космических аппаратов
Афанасьев Евгений Васильевич
Гидросистемы и гидромашины
Курс лекцийЛекция № 1
ВВЕДЕНИЕ
СВОЙСТВА ЖИДКОСТЕЙ
ПРЕДМЕТ ГИДРАВЛИКИ
Прикладную часть гидромеханики, для которой характерен определенный круг технических вопросов, задач и методы их разрешения, называют гидравликой.… В гидравлике рассматриваются главным образом потоки жидкости, ограниченные и… Термин “жидкость” в гидромеханике имеет более широкий смысл, чем это принято в обыденной жизни. В понятие “жидкость”…СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЖИДКОСТЬ.
ДАВЛЕНИЕ В ЖИДКОСТИ
Вследствие текучести жидкости в ней не могут действовать сосредоточенные силы, а возможно лишь действие сил, непрерывно распределенных по ее объему… Массовые силы пропорциональны массе жидкого тела, или, для однородных… Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны…Рис. 1.1
Как массовые, так и поверхностные силы в гидромеханике рассматривают обычно в виде единичных сил, т.е. сил, отнесенных к соответствующим единицам. Массовые силы относят к единице массы, а поверхностные - к единице площади. Так как массовая сила равна произведению массы на ускорение, то единичная массовая сила численно равна ускорению.
Единичная поверхностная сила, называемая напряжением поверхностной силы, как и всякая сила, раскладывается на нормальное и касательное напряжения. Нормальное напряжение, т. е. напряжение силы давления, называется гидромеханическим давлением или просто давлением и обозначается буквой p.
Если сила давления DP равномерно распределена по площадке DS, то давление определяют по формуле
 (1.1)
(1.1)
В общем случае давление в данной точке равно пределу, к которому стремится отношение силы давления к площади, на которую она действует, при стремлении величины площадки к нулю, т. е. при стягивании площадки в точку
 (1.2)
(1.2)
Если давление отсчитывается от нуля, то оно называется абсолютным, а если отсчитывается от атмосферного, то его называют избыточным или манометрическим. Следовательно Pабс=Pа+Pизб. За единицу давления в международной системе единиц (СИ) принято равномерно распределенное давление, при котором на площадь 1 м2 действует сила 1 ньютон, т. е. 1 н/м2 = 1 Па. В технике продолжают применять внесистемную единицу – техническую атмосферу.
1 атм. = 1 кГ/см2 = 9,81* 104 Па
Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой t и выражается подобно давлению пределом
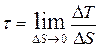 (1.3)
(1.3)
единицы его измерения те же, что и для давления.
Лекция №2
ОСНОВНЫЕ СВОЙСТВА КАПЕЛЬНЫХ ЖИДКОСТЕЙ
кг/м3 (1.4) где М – масса жидкости в объеме W. Удельным весом g называют вес единицы объема жидкости, т. е.Рис. 1.2
Скорость движения слоев v уменьшается по мере уменьшения расстояния до стенки yвплоть до v=0 при y=0, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений. Согласно гипотезе, высказанной впервые Ньютоном, касательное напряжение в жидкости зависит от ее рода и характера течения и при слоистом течении изменяется прямо пропорционально так называемому поперечному градиенту скорости; в соответствии с этим для безграничной стенки будем иметь
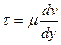 (1.12)
(1.12)
где m – коэффициент пропорциональности, получивший название динамического коэффициента вязкости жидкости;
dv – приращение скорости, соответствующее приращению координаты dy (рис. 1.2.).
Поперечный градиент скорости dv/dy определяет собой изменение скорости, приходящееся на единицу длины в направлении y и, следовательно, характеризует интенсивность сдвига слоев жидкости в данной точке.
В случае постоянства касательного напряжения по поверхности S полная касательная сила (сила трения), действующая по этой поверхности, равна
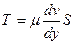 (1.13)
(1.13)
Для определения размерности коэффициента вязкости решим уравнение (1.12) относительно m, в результате получим
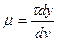 н×с/м2
н×с/м2
В системе СГС за единицу вязкости принимается
1 пуаз = 1 дина×с/см2=0,1 н×с/м2
Наряду с динамическим коэффициентом вязкости m применяют еще так называемый кинематический коэффициент вязкости
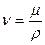 (1.14)
(1.14)
В качестве единицы измерения кинематического коэффициента вязкости употребляется 1 стокс = 1 см2/с. Сотая доля стокса называется сантистоксом. В системе СИ размерность n - м2/с. Отсутствие размерности силы в размерности этой величины и послужило поводом к названию ее кинематическим коэффициентом вязкости.
Вязкость капельных жидкостей зависит от температуры, уменьшаясь с увеличением последней. Вязкость газов с ростом температуры увеличивается.
Это объясняется различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает. В газах же вязкость обусловлена главным образом беспорядочным тепловым движением молекул, интенсивность которого увеличивается с ростом температуры. Характерные кривые изменения вязкости от температуры приведены на рис. 1.3.

|
Рис. 1.3
Влияние температуры на вязкость жидкости можно оценивать следующей формулой

где m и m0 – значения вязкости при температурах T и T0;
l - коэффициент, значение которого для масел меняется
в пределах 0,02 – 0,03.
Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления, порядка нескольких сотен кГ/см2.
Из закона трения, выражаемого уравнением (1.12), следует, что напряжения трения возможны только в движущейся жидкости, т. е. вязкость жидкости проявляется при ее течении. В покоящейся жидкости касательные напряжения будем считать равными нулю.
6. Испаряемость. Это свойство присуще всем капельным жидкостям.
Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении: чем выше температура кипения, тем меньше испаряемость жидкости. В гидросистемах нормальное атмосферное давление является лишь частным случаем; обычно приходится иметь дело с испарением, а иногда и кипением жидкостей в замкнутых объемах при различных температурах и давлениях. Поэтому более полной характеристикой испаряемости является давление насыщенных паров pn, выраженное в функции температуры. Чем больше давление насыщенных паров при данной температуре, тем больше испаряемость жидкости. С увеличением температуры давление pn увеличивается, однако у разных жидкостей в разной степени. Конкретные данные можно найти в справочной литературе по теплофизическим свойствам жидкостей.
7. Растворимость газов в жидкостях происходит при всех условиях, но количество растворенного газа в единице объема жидкости различно для разных жидкостей и изменяется с увеличением давления. Относительный объем газа, растворимого в жидкости до ее полного насыщения, можно считать прямо пропорциональным давлению, т. е.
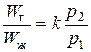
где Wг – объем растворенного газа при нормальных условиях;
Wж – объем жидкости;
p1 и p2 – начальное и конечное давление газа.
Коэффициент k растворимости воздуха имеет следующие значения при 200 С: для воды – 0,016, для жидкости АМГ–10 – 0,104.
При понижении давления в жидкости происходит выделение растворенного в ней газа, причем газ выделяется из жидкости интенсивнее, чем растворяется в ней. Это явление может отрицательно сказываться на работе гидросистем.
Лекция № 3
ГИДРОСТАТИКА
СВОЙСТВА ГИДРОСТАТИЧЕСКОГО ДАВЛЕНИЯ
Гидростатическое давление в жидкости имеет следующие два свойства: 1. На внешней поверхности гидростатическое давление всегда направлено по… Это свойство непосредственно вытекает из определения давления как напряжения от нормальной сжимающей силы. Под внешней…ОСНОВНОЕ УРАВНЕНИЕ ГИДРОСТАТИКИ
Рис. 2.2ПЬЕЗОМЕТРИЧЕСКАЯ ВЫСОТА. ВАКУУМ. ИЗМЕРЕНИЕ ДАВЛЕНИЯ
Пьезометрическую высоту, соответствующую избыточному давлению, можно наблюдать в так называемом пьезометре – простейшем устройстве для измерения… Рис. 2.3Рис. 2.4
Жидкость будет следовать за поршнем и вместе с ним поднимется на некоторую высоту h от свободной поверхности с атмосферным давлением. Так как для точек, расположенных под поршнем, глубина их погружения относительно свободной поверхности отрицательна, то согласно уравнению (2.1), абсолютное давление жидкости под поршнем
 (2.4)
(2.4)
а величина вакуума

По мере подъема поршня абсолютное давление жидкости под поршнем уменьшается. Нижним пределом абсолютного давления в жидкости является нуль, а максимальное значение вакуума численно равно атмосферному давлению, поэтому максимальная высота всасывания жидкости определится из уравнения (2.4), если в нем положить p = 0 (точнее, p = pn). Таким образом, без учета упругости паров
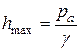 2.5)
2.5)
При нормальном атмосферном давлении (1,033 кГ/см2) высота hmax равна: для воды 10,33 м, для ртути 760 мм.

|
Простейшим устройством для измерения вакуума может служить стеклянная трубка, показанная на рис. 2.5 в двух вариантах.
Рис. 2.5
Вакуум в жидкости может измеряться либо с помощью U – образной трубки, либо путем использования перевернутой U – образной трубки, один конец которой опущен в сосуд с жидкостью.
Для измерения давления жидкостей и газов помимо пьезометров пользуются манометрами, которые делятся на жидкостные, механические и электрические. Подробные сведения о данных приборах можно найти в специальной литературе.
Лекция №4
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА ПЛОСКУЮ СТЕНКУ
Используем основное уравнение гидростатики (2.1) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.6).
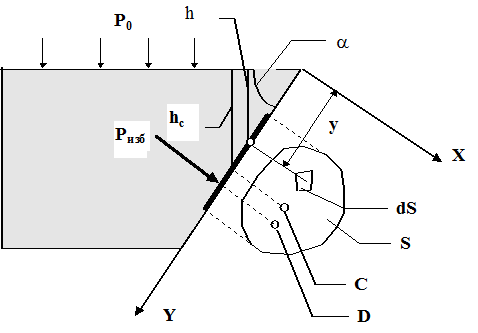
|
Рис. 2.6
Вычислим полную силу P давления, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
Ось 0x направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось 0y – перпендикулярно этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:
 ,
,
где p0 – давление на свободной поверхности;
h – глубина расположения площадки dS.
Для определения полной силы P выполним интегрирование по всей площади S.
 ,
,
где y – координата центра площадки dS.
Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси 0x и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.

Следовательно,
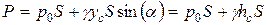
(здесь hc – глубина расположения центра тяжести площади S), или
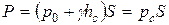 (2.6)
(2.6)
т. е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади.
Найдем положение центра давления. Так как внешнее давление p0 передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, согласно которому момент равнодействующей силы давления относительно оси 0x равен сумме моментов составляющих сил, т. е.
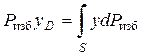
где yD – координата точки приложения силы Pизб.
Выражая Pизб и dPизб через yc и y и определяя yD, получим

где  - момент инерции площади S относительно оси 0x.
- момент инерции площади S относительно оси 0x.
Учитывая, что 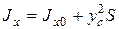
(Jx0 – момент инерции площади S относительно центральной оси, параллельной 0x), получим
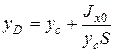 (2.7)
(2.7)
Таким образом, точка приложения силы Pизб расположена ниже центра тяжести площади стенки; расстояние между ними равно
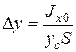
Если давление p0 равно атмосферному, и оно действует с обеих сторон стенки, то точка D и будет центром давления. Когда же p0 выше атмосферного, то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: hcgS и p0S. При этом, чем больше вторая сила по сравнению с первой, тем ближе центр давления к центру тяжести площади S.
В частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится из геометрических соображений. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.7), центр тяжести которого отстоит от основания на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на том же расстоянии от основания.
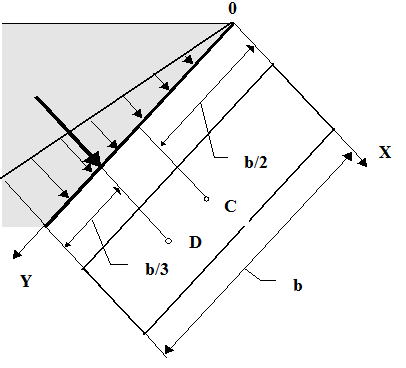
|
Рис. 2.7
В машиностроении часто приходится сталкиваться с действием силы давления на плоские стенки, например на стенки поршней или цилиндров гидравлических машин. Обычно p0 при этом бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки.
СИЛА ДАВЛЕНИЯ ЖИДКОСТИ НА КРИВОЛИНЕЙНЫЕ СТЕНКИ. ЗАКОН АРХИМЕДА.
Сила давления жидкости в этих случаях приводится к равнодействующей силе, лежащей в плоскости симметрии. Возьмем цилиндрическую поверхность AB с образующей, перпендикулярной плоскости…Рис. 2.8
В случае “а” выделим объем жидкости, ограниченный рассматриваемой поверхностью AB, вертикальными поверхностями, проведенными через границы этого участка, и свободную поверхность жидкости, т. е. объем ABCD. Рассмотрим условия равновесия этого объема в вертикальном и горизонтальном направлениях. Если жидкость действует на поверхность AB с силой P, то поверхность AB действует на жидкость с силой P, направленной в противоположную сторону. На рис. 2.8 показана эта сила реакции, разложенная на две составляющие: горизонтальную Pг и вертикальную Pв.
Условие равновесия объема ABCD в вертикальном направлении имеет вид
 (2.8)
(2.8)
где p0 – давление на свободной поверхности жидкости;
Sг – площадь горизонтальной проекции поверхности AB;
G – вес выделенного объема жидкости.
Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности EC и AD взаимно уравновешиваются, и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверхности AB – Sв.
 (2.9)
(2.9)
Определив по формулам (2.8) и (2.9) вертикальную и горизонтальную составляющие, найдем полную силу давления P
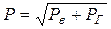
В том случае, когда жидкость расположена снизу, величина гидростатического давления во всех точка поверхности AB имеет тоже значение, что и в предыдущем случае, только направление его будет противоположным. Суммарные силы Pв и Pг, определяются по тем же формулам, но с обратным знаком. При этом под величиной G следует понимать вес жидкости в объеме ABCD, хотя он, и не заполнен жидкостью. Положение центра давления на цилиндрической стенке может быть найдено, если известны Pв и Pг и определены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача облегчается, если рассматриваемая цилиндрическая поверхность является круговой. Тогда равнодействующая сила пересекает ось поверхности, это следует из того, что элементарная сила давления нормальна к поверхности, т. е. направлена по радиусу. Изложенный способ определения силы давления применим также и к сферическим поверхностям. Применим описанный выше прием для доказательства закона Архимеда.
Пусть в жидкость погружено тело произвольной формы объемом W (рис. 2.9).
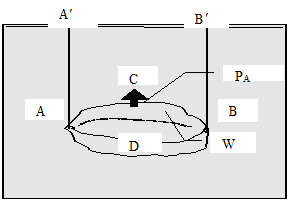
|
Рис. 2.9
Спроектируем это тело на свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела по замкнутой кривой. Эта кривая отделяет верхнюю часть тела ACB от нижней ее части ADB. Вертикальная составляющая силы избыточного давления жидкости на верхнюю часть поверхности тела направлена вниз и равна весу жидкости в объеме AA¢B¢BCA. Вертикальная составляющая силы избыточного давления жидкости на нижнюю часть поверхности тела направлена вверх и равна весу жидкости в объеме AA¢B¢BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело PA будет направлена вверх и равна весу жидкости в объеме W тела. В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.
Лекция №5
2.6. ПРЯМОЛИНЕЙНОЕ РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ СОСУДА С ЖИДКОСТЬЮ Ранее мы рассматривали равновесие жидкости под действием лишь одной массовой… Если сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости помимо…РАВНОМЕРНОЕ ВРАЩЕНИЕ СОСУДА С ЖИДКОСТЬЮ
На жидкость в этом случае будут действовать две массовые силы, сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы,… Рис. 2.11Лекция № 6
КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
Уравнение Бернулли для струйки идеальной жидкости
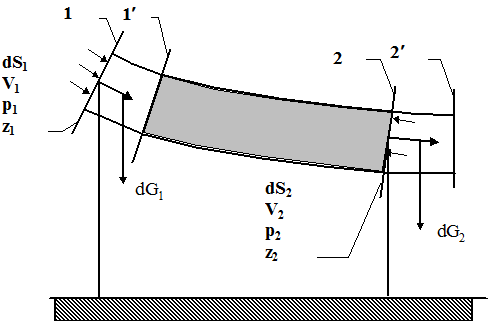
Рассмотрим установившееся течение жидкости, находящейся под воздействием только одной массовой силы - веса жидкости.
|
Выделим в потоке струйку, такую малую, что изменением параметров в ее поперечном сечении можно пренебречь и считать их постоянными.
Рис. 3.1
За бесконечно малый промежуток времени Dt участок струйки 1- 2переместится в положение 1¢- 2¢.
Применим к этой струйке уравнение энергии, заключающееся в том, что работа сил по перемещению струйки равна приросту кинетической энергии этой струйки.
Известно, что элементарная работа силы определяется выражением
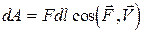
Работа поверхностных сил давления тогда составит
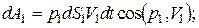

Т. к. в первом сечении направление сил давления совпадает с направлением вектора скорости, а во втором сечении оно противоположно, то
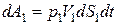

Заметим, что работа сил давления, действующих по боковым поверхностям струйки равна 0, вследствие ортогональности векторов давления и скорости.
Суммарная работа поверхностных сил определится выражением
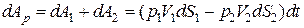
Элементарная работа массовых сил (сил веса) определяется изменением потенциальной энергии выделенного элемента массы
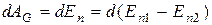
Потенциальная энергия массы, заключенной в объеме W определяется выражением
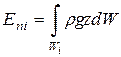
Учитывая, что для несжимаемой жидкости r= const, получим
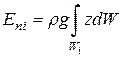
Объем, занимаемый струйкой в начальном и конечном положениях можно представить в виде двух составляющих, рис. 3.1.
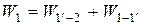

Масса жидкости, заключенная в объемах W1 и W2 определится как
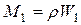

Т. к. приток массы в рассматриваемой струйке отсутствует, то
M1 = M2
следовательно
W1 = W2
Нетрудно заметить, что объем 1¢-2 для рассматриваемых положений является общим, тогда
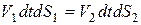
или

Это выражение определяет закон сохранения массы для струйки несжимаемой жидкости.
С учетом отмеченного

где dG = rgdW - элементарный вес жидкости, заключенный в объеме dW.
Т. е.

Применяя такой же прием, получим выражение для прироста кинетической энергии струйки
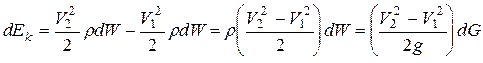
Запишем уравнение баланса энергии

Подставляя имеющиеся выражения в данную формулу, получим
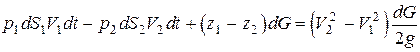
после преобразований, с учетом того, что dW1 = dW2 =dW =dG/g, получаем
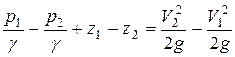
или, после перегруппирования членов
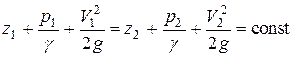
Это выражение и представляет собой уравнение Бернулли для идеальной несжимаемой жидкости.
Величина  называется скоростным напором,
называется скоростным напором,  определена ранее как гидростатический напор, а величина
определена ранее как гидростатический напор, а величина  получила название полный напор.
получила название полный напор.
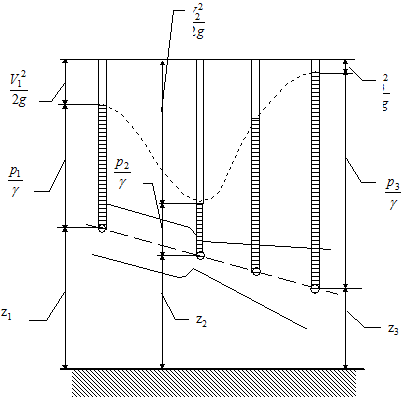
|
Таким образом, согласно уравнению Бернулли, полный напор представляет собой сумму гидростатического и скоростного напора и для выделенной струйки жидкости это величина постоянная. Проиллюстрируем это положение графиком, см. рис. 3.2.
Рис. 3.2
Лекция №7.
Уравнение Бернулли для реальной вязкой жидкости.
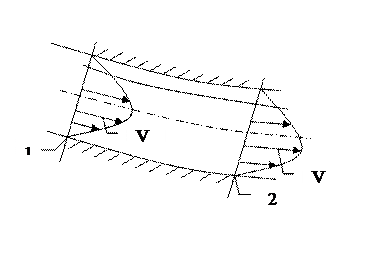
Рис. 3.3
Будем считать, что по всему поперечному сечению  . Строго говоря это утверждение справедливо только для параллельных трубок тока.
. Строго говоря это утверждение справедливо только для параллельных трубок тока.
Выделим в общем потоке элементарную струйку, такую тонкую, что изменением параметров в поперечном сечении будем пренебрегать. От трубки к трубке параметры потока будем считать переменными.
Введем понятие элементарной мощности потока, которая переносится элементарной струйкой dN.
Известно, что 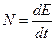 , тогда
, тогда 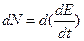 ; Учитывая, что
; Учитывая, что 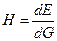
Получим  , но
, но 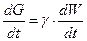 , а
, а 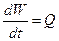 ; где Q – объемный расход жидкости, а γ – удельный вес. Тогда
; где Q – объемный расход жидкости, а γ – удельный вес. Тогда 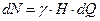 ,
, 
Мощность всего потока определится как 
Пользуясь теоремой о среднем: 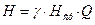
 (3.1)
(3.1)
 ;
;
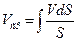 ;
;
Подставляя в (3.1), получим
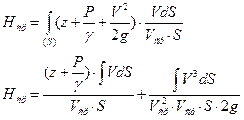
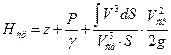 (3.2)
(3.2)
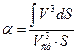 - коэффициент неравномерности потока. (3.3)
- коэффициент неравномерности потока. (3.3)
Экспериментально установлено следующее:
 (3.4)
(3.4)
ΣΔhi – суммарные потери полного напора в канале между сечениями 1 и 2.
Уравнение (3.4) – это уравнение Бернулли для реальной вязкой жидкости.
развернутая форма уравнения Бернулли: 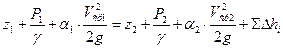
– в каждом сечении мы должны найти среднее значение V и значение коэффициента неравномерности потока α.
Краткие сведения с потерях полного напора.
1. потери, связанные с трением, для их существования необходима характерная длина канала; 2. потери, связанные с формообразованием жидкости (местные потери). Оба вида потерь могут быть оценены с помощью универсальной формула ВейсбахаРис. 3.4
 , постоянную можно найти по известным граничным условиям
, постоянную можно найти по известным граничным условиям 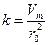 ; тогда средняя скорость такого потока составит:
; тогда средняя скорость такого потока составит:
 ;
;
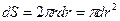 ;
;
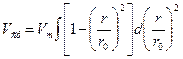 ;
;


Определим значение коэффициента неравномерности данного потока
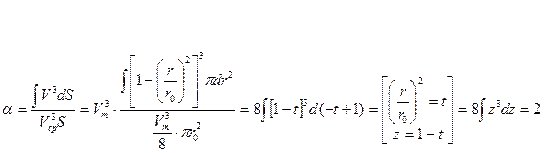
Развернутая форма уравнения Бернулли для такого потока будет иметь вид:
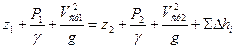
при 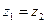 для канала постоянного сечения
для канала постоянного сечения 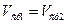 ;
;
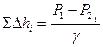 .
.
Лекция №8.
Уравнение Бернулли для относительного движения.
1. Случай прямолинейного равноускоренного движения (рис. 3.5).

Рис. 3.5
Перемещая этот канал на движущийся объект, который движется с постоянным ускорением ā, появляется инерционная составляющая Δhин.

 ; где а – модуль ускорения, g – ускорение свободного падения.
; где а – модуль ускорения, g – ускорение свободного падения.
Правило знаков: Если проекция вектора ā на ось канала направлена от первого сечения ко второму, то берется знак «+».
2.
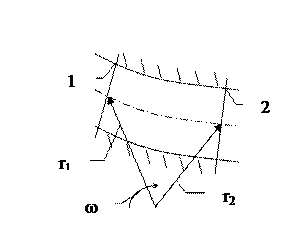 |
Случай вращательного движения (рис. 3.6).
Рис. 3.6

Применение уравнения Бернулли для решения практических задач
 |
Задача о расходомере. Рассмотрим движение жидкости в сужающемся круглом канале (рис. 3.7).
Рис. 3.7
Примем α1=α2 ≈ 1,0.
Учитывая, что α1=α2 ≈ 1,0, Vср1→V1, аналогично для Vср2.
Запишем уравнение Бернулли:
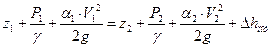 ;
;
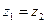 ;
;  ;
; 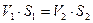
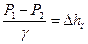
Тогда  .
.
Зная, что  , получим
, получим  .
.
 , т.к.
, т.к. 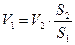
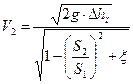
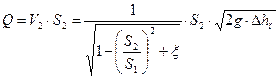
Обозначим 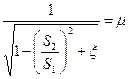 коэффициент расхода .
коэффициент расхода .
 .
.
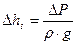 →
→ 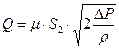 формула расхода для дросселя.
формула расхода для дросселя.
Лекция № 9
Режимы течения жидкости в трубах и основы подобия.
1. Ламинарное ( слоистое течение ) 2. Турбулентное ( бурное, возмущенное ) При ламинарном режиме течения жидкость движется без перемешивания слоев, плавно изменяя скорость, может быть…Лекция№10.
Ламинарный режим течения в круглой трубе.

Рис. 4.1
Рассмотрим установившееся ламинарное течение в канале (рис. 4.1).
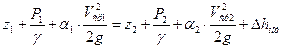 (4.1)
(4.1)
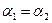 , тогда
, тогда 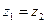 ,
,  ,
, 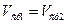 .
.
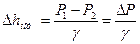
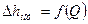
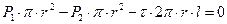
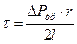 (4.2)
(4.2)
где ΔРтр – перепад давлений, обусловленный силами трения.
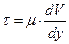 (4.3)
(4.3)
Т.к. dy=-dr (рис. 4.1) то 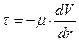 (4.4)
(4.4)
 ;
;

 ;
;
 (5);
(5);  ;
;  (6);
(6);
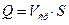 ;
;  ;
;
 ;
; 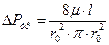 ;
;
т.к. 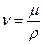 ,
, 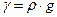 ; имеем
; имеем 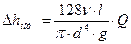 - уравнение Пуазейля.
- уравнение Пуазейля.
В установившемся ламинарном течении потери полного напора вызванные трением прямо пропорциональны расходу (средней скорости) жидкости.
Противоречие, возникающее из формулы Вейсбаха
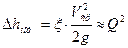 ;
;
Легко устраняется, если положить, что  ;
;
Из формулы Дарси следует, что 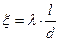 -.
-.
Тогда  ;
;
и 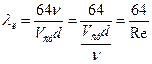 ;
;
получаем выражение для коэффициента трения при ламинарном течении
λл=64/Re (4.5)
Начальный участок ламинарного течения.
 |
Рассмотрим истечение жидкости в канал из бака бесконечного объема.
Рис. 4.2
Эпюры скорости в каждом сечении имеют вид:

Рис. 4.3
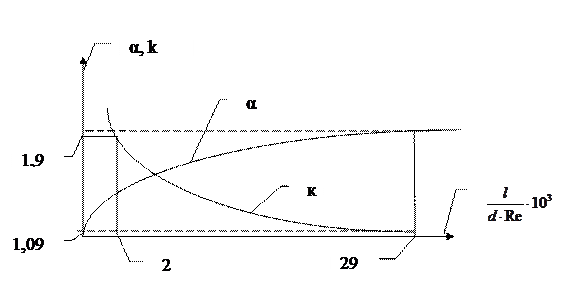 |
Протяженность начального участка может быть определена по формуле Шиллера:
 , а коэффициент трения λ = k λл, значения k берутся из графика (рис. 4.4)
, а коэффициент трения λ = k λл, значения k берутся из графика (рис. 4.4)
Рис. 4.4
Особые случаи ламинарного течения.
 |
Течение с теплоотводом.
Рис. 4.5
Течение с теплоподводом.
Оценка коэффициента трения  νст определяется при Тст
νст определяется при Тст
νж определяется по средней температуре жидкости Тж.
Течение в капиллярах. Смачиваемые пары увеличивают, а несмачиваемые уменьшают потери полного напора.
Явление облитерации (заращивания).
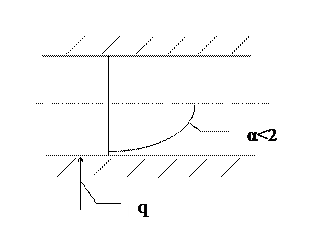 |
Рис. 4.6
Наблюдается при протекании ряда рабочих жидкостей через узкие щели и отверстия. Очень часто в качестве рабочей жидкости гидравлической системы используются продукты перегонки нефти (газолин). Для улучшения смазывающих свойств газолина в него добавляют специальные вещества, которые называются присадки. Полимерные присадки способствуют явлению облитерации.
С ростом давления заращивание протекает интенсивней, а с ростом температуры этот процесс ослабевает.
Лекция №11.
Турбулентное течение в каналах постоянного сечения.
 |
Характерная зависимость потерь полного напора для различных режимов течения приводятся на рис. 4.7.
Рис. 4.7
Оценка производится по формулам Вейсбаха и Д’ арси  ,
, 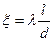
При больших Re 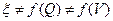 , Δhт ˜ Q2 , это автомодельное течение.
, Δhт ˜ Q2 , это автомодельное течение.
Коэффициент трения для турбулентного режима течения оценивается по формуле Блазиуса 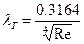 при Re < 105
при Re < 105
 |
или Конакова
 при Re < 107
при Re < 107
Турбулентное течение в шероховатых трубах.
Гладкие трубы: - трубы из цветных металлов и нержавеющей стали; - трубы из черных металлов, не имеющие сварных соединений и полученные вытяжкой.Рис. 4.8
Расчет потерь полного напора в некруглых трубах.
Для турбулентного режима течения в гидравлике используется прием, позволяющий определить потери полного напора в канале с произвольной формой… Гидравлический радиус – отношение поперечного сечения канала (S), по которому… Для круглой трубы , тогда ,Лекция №12
Местные сопротивления.
В гидравлике местные сопротивления делятся на 2 группы:
1. Внезапные.
2. Постепенные (плавные).
В каждую группу входят:
· Расширение
· Сужение
· Поворот
Внезапное расширение канала.
 |
Рис. 5.1
Рассматривается турбулентный режим течения
Коэффициент внезапного расширения:  ,
, 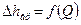
Для идеальной жидкости: 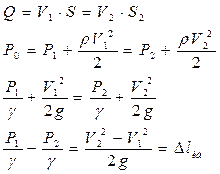
Δl>Δlид
Потери полного давления при внезапном расширении Δhвр
Примем следующие допущения:
1. α1=1, α2=1 - турбулентное течение
2. τ=0 касательными напряжениями пренебрегаем из-за малой длины
3. Р=Р1 давление на боковой стенке (эксперимент).
Тогда
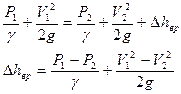
Для контура, ограниченного сечениями 1-1, 1-2 и боковой стенкой канала запишем уравнения сохранения количества движения в проекции на ось канала:

Учитывая уравнения неразрывности V1S1=V2S2, после преобразований получим
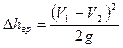 (5.1)
(5.1)
Эта формула носит наименование теоремы Борда-Карно.
Вводя понятие степени расширения канала n = S2/S1, будем иметь

Тогда коэффициент сопротивления
 (5.2)
(5.2)
Этот результат хорошо согласуется с опытами.
Лекция №13.
Постепенное расширение канала. Диффузор
Определим коэффициент местных потерь диффузора. Представив, что потери полного напора складываются из двух составляющих. Потери на трение и потери… VS=const VS=V1S1,Лекция №14.
Гидравлический удар.
Рис. 6.1. аРис. 6.1. б
Если это упругая идеальная колебательная система, то этот процесс повторится и будет длиться бесконечно. В действительности быстро затухает из-за диссипации энергии.
При гидравлическом ударе происходит преобразование кинетической энергии жидкости в энергию деформации трубопровода и энергию деформации жидкости.
Ек = Едт + Едж (6.1)
 (6.2)
(6.2)
Здесь R – радиус канала, V0 – скорость потока жидкости. Мы рассматриваем жидкость как сжимаемую среду, но с другой стороны эти изменения плотности столь малы, что мы можем этим пренебречь. Энергия деформации определится по (6.3).
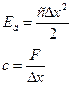 (6.3)
(6.3)
Для трубопровода

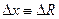


По Ламэ определим максимальные тангенциальные напряжения
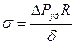
После преобразований получим
 (6.4)
(6.4)
Для жидкости 
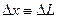

Но 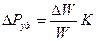
 (6.5)
(6.5)
Подставляя 6.2, 6.4 и 6.5 в 6.1, после преобразований получим:
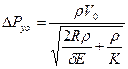 (6.6)
(6.6)
Впервые это выражение получено Н.Ф. Жуковским. Если считать, что трубопровод абсолютно жесткий, то получим более простую формулу для оценки максимального давления при гидроударе 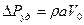
ГИДРОСИСТЕМЫ И ГИДРОМАШИНЫ
Лекция №15
Общие сведения о гидропередачах
Многие современные сложны машины общего и специального назначения буквально насыщены различными гидравлическими системами и агрегатами, которые по их назначению и выполняемым функциям принято подразделять на две основные группы:
1. Системы и агрегаты, предназначенные для передачи механической энергии от какого-либо источника к рабочим органам машины и управления движением этих органов;
2. Системы и агрегаты, предназначенные для перемещения различных жидкостей из мест хранения к местам ее потребления.
Системы и агрегаты первой группы получили общее название “гидропередачи”, а системы и агрегаты второй группы, в общем случае, можно называть “насосными станциями”.
В задачу настоящего курса входит изучение только тех устройств и агрегатов, которые относятся к первой группе, т.е. к гидропередачам. Дело в том, что гидропередачи в общем случае сложнее систем и устройств, относящихся к группе насосных станций.
В общем случае гидропередачей следует называть механизм, который позволяет передавать механическую энергию от какого-либо источника к рабочему органу той или иной машины посредством жидкости.
Таким образом, основная функция гидропередач аналогична функциям других широко известных и исторически ранее появившихся механических передач: ременной, шестеренной, цепной, червячной, кривошипно-шатунной и т. п.
Учитывая, что в любой гидропередаче происходит двукратное преобразование энергии (вначале механическая энергия преобразуется в энергию потока жидкости, а затем на выходе энергия потока преобразуется обратно, в механическую), закономерно, по аналогии, например, с электрическими системами, называть ее гидроприводом.
Таким образом, под термином “гидропривод” мы будем понимать достаточно сложную гидропередачу, позволяющую не только передавать механическую энергию от какого-либо источника к рабочему органу машины, но и управлять движением этого органа.
То есть любой гидропривод можно назвать гидропередачей, но не всякая гидропередача может быть названа гидроприводом.
По принципу действия гидропередачи вообще, и гидроприводы в частности, подразделяются на:
а) статические или объемные;
б) динамические;
в) импульсные или волновые.
Статическиминазываются гидропередачи, у которых напорная линия всегда геометрически отделена от всасывающей, а усилия на рабочих органах определяются главным образом статическим давлением жидкости в магистралях. Все узлы таких гидропередач находятся, примерно, на одном уровне, а скорость течения жидкости в рабочих каналах относительно мала (от 1 до 10 м/с).
Динамическими называются такие гидропередачи, которые передают энергию посредством гидродинамического эффекта потока жидкости. То есть величина усилий на рабочих органах этих гидропередач определяется главным образом скоростным напором. В рабочей части этих машин скорость потока жидкости достигает десятков метров в секунду. При этом герметичность (геометрическое разделение) между всасывающей и нагнетающей полостями отсутствует.
Импульсными или волновыми называются передачи, передающие энергию импульсами. Величина усилий на рабочих органах этих агрегатов в одинаковой степени зависит как от скорости движения потока жидкости, так и от статического давления в магистралях.
В данном курсе рассматриваются только статические гидропередачи и их элементы, как наиболее распространенные в специальной технике. Поэтому в дальнейшем для краткости изложения слово “статические”, как правило, будет опускаться.
Устройство и действие статических гидропередач

|
Рассмотрим простейший механизм (рис.7.1), состоящий из двух сообщающихся цилиндров, в которых размещены поршни со штоками, а пространство между поршнями залито вязкой жидкостью. При этом в процессе рассуждений, трением в подвижных сочленениях, усилием возвратной пружины и утечками жидкости из цилиндров будем пренебрегать.
Рис. 7.1 Принципиальная схема статической гидропередачи
Если шток с поршнем узла (1) переместить на расстояние L1, то, при принятых допущениях нетрудно убедиться, что поршень со штоком узла (2) переместится на расстояние  . При этом усилие F1, необходимое для перемещения поршней бесконечно мало. Однако, если шток узла (2) упрется в какое-то препятствие, например, вращающийся вал, то, развив усилие F1 на педали штока (1), получим, что вал будет нагружен силой
. При этом усилие F1, необходимое для перемещения поршней бесконечно мало. Однако, если шток узла (2) упрется в какое-то препятствие, например, вращающийся вал, то, развив усилие F1 на педали штока (1), получим, что вал будет нагружен силой  . Таким образом, механизм передает движение и силу. Известно, что произведение силы на скорость есть мощность, т.е. механизм при помощи жидкости передает энергию от источника к объекту (валу, который надо затормозить). Таким образом, этот механизм удовлетворяет общему определению гидропередачи (передача энергии посредством жидкости).
. Таким образом, механизм передает движение и силу. Известно, что произведение силы на скорость есть мощность, т.е. механизм при помощи жидкости передает энергию от источника к объекту (валу, который надо затормозить). Таким образом, этот механизм удовлетворяет общему определению гидропередачи (передача энергии посредством жидкости).
Для удовлетворения понятию “статическая гидропередача”, должно быть выполнено условие геометрического отделения полости нагнетания от полости всасывания. Здесь, правда, полость одна. Но она попеременно выполняет функции, то полости нагнетания, то полости всасывания. Таким образом, геометрическое разделение полостей обеспечивается временной паузой. То есть подобный простейший механизм полностью соответствует данному ранее определению понятия статической гидропередачи.
Рассматривая представленный на рис.7.1 механизм легко заметить, что узлы (1) и (2) в принципе конструктивно одинаковы и обратимы. Следовательно, для образования статической гидропередачи непрерывного, например, вращательного движения можно взять два одинаковых насоса, соединить их полости трубопроводами, залить жидкостью, и вал одного насоса соединить с источником энергии, а другого с нагрузкой (рис. 7.2). Если насос и гидромотор (ГМ) нерегулируемы, имеют одинаковые рабочие объемы, то такая гидропередача будет выполнять функцию гидравлического вала или гидравлической муфты. Если рабочие объемы насоса и гидромотора
|
различны, то это будет либо гидравлический редуктор, либо гидравлический мультипликатор.
Применять на практике такие агрегаты, как правило, нецелесообразно из-за относительной дороговизны гидравлических машин. Однако нет правил без исключений, в жизни могут встретиться и такие ситуации, когда подобное решение будет самым рациональным (например, передать вращение от электродвигателя (ЭД), размещенного в трюме к какому-то механизму, расположенному на 2-5 палубе).
Если же взять насос (или ГМ) регулируемым (рис.7.3), то получим гидропривод вращательного движения, ибо такой агрегат уже способен после запуска ЭД и без его остановки запускать или останавливать управляемый объект (J0), реверсировать его движение и регулировать скорость.
Таким образом, любая гидропередача в принципе должна состоять как минимум из 2-х элементов: насоса, преобразующего механическую энергию какого-либо источника в энергию потока жидкости и гидродвигателя, соединенного с насосом соответствующими каналами и преобразующего энергию потока жидкости обратно в механическую.
Для гидропривода в нашем понимании обязательно наличие управляюще-регулирующего устройства, которое может быть выполнено в виде неотъемлемой составной части насоса или гидродвигателя (а также того и другого), или в виде отдельных специальных механизмов (дросселя с переливным клапаном - распределителем).
Наличие различных вспомогательных устройств, как-то предохранительных клапанов, обратных клапанов, фильтров, гидрозамков, ограничителей мощности и т.п. определяется конкретным назначением гидропередачи (гидропривода) и требованиями, предъявляемыми к ней (к нему). То есть наличие этих элементов в системе не определяет принцип действия статической гидропередачи.
|
Классификация статических гидропередач
7.2.1. По назначению различают:
а) силовые гидропередачи, предназначенные главным образом для передачи механической энергии от какого-либо источника к рабочему органу машины трансформации момента или силы и изменения скорости движения рабочего органа;
б) гидравлические системы управления и автоматики, предназначенные главным образом для передачи движения и усиления входного командного сигнала.
К силовым гидропередачам относятся гидравлические приводы вертикального и горизонтального наведения многих пусковых и артиллерийских установок, гидравлические подъемные и подъемно - уравновешивающие механизмы, современные механизмы вывешивания и горизонтирования самоходных агрегатов и многие другие гидравлические механизмы.
К гидравлическим системам управления и автоматики обычно относят гидравлические усилители различных типов, гидравлические суппорты металлорежущих станков, гидравлические рулевые машины самолетов, гидропривод рулей тяжелых автомобилей, гидравлические системы торможения, стопорения и тому подобные механизмы.
В состав многих современных гидравлических агрегатов входят как силовая часть, так и гидравлическая система управления и автоматики. Т. е. в таких агрегатах имеется не менее двух, трех гидравлических контуров, завязанных прямыми и обратными связями, и такие агрегаты чаще всего называют гидравлическими или электрогидравлическими следящими приводами (ГСП или ЭГСП).
По устройству и внешнему конструктивному оформлению силовые гидропередачи и гидравлические системы управления и автоматики в принципе могут быть одинаковыми. Однако по ряду параметров и некоторым деталям они существенно различны. Например, силовые гидропередачи, как правило, работают при высоких давлениях (10-30) МПа и имеют высокий кпд (более 0,6-0,75) , системы автоматики и управления работают при сравнительно низких (до 2,5 МПа) давлениях, к ним предъявляются очень высокие требования по точности передачи командного сигнала, а по кпд требования не высокие (порядка 0,2).
7.2.2. По характеру движения различают:
а) вращательные или ротационные;
б) возвратно-поступательные;
в) поворотные.
Этот классификационный признак в значительной степени условен, т.к. учитывает характер движения лишь выходного звена гидропередачи. (входное звено в 99 случаях из 100 имеет вращательное движение - исключение составляют гидравлические тормозные устройства). Вместе с тем этот признак весьма практичен, что позволяет специалистам одним-двумя словами характеризовать принципиальные конструктивные особенности основных элементов гидропередачи.
7.2.3. По способу регулирования различают гидроприводы:
а) с объемным регулированием,
б) с дроссельным регулированием,
с) со ступенчатым регулированием.
Сущность объемного регулирования заключается в бесступенчатом изменении производительности насоса (или рабочего объема гидродвигателя) в процессе его работы. Изменять производительность насоса, при постоянстве скорости вращения его вала, можно тремя путями: изменением длины рабочего хода замыкателя (поршня или пластины), изменением эффективной величины зон нагнетания и всасывания в распределителе и изменением величины сдвига фаз работающих попарно замыкателей.
Гидроприводы с объемным регулированием являются наиболее сложными гидравлическими агрегатами и с точки зрения КПД наиболее совершенными. Впервые их стали использовать в военной технике, которая и в настоящее время является одним из основных потребителей этих машин.
Объемное регулирование присуще, как правило, силовому приводу. Наиболее характерным признаком этого способа регулирования является то, что упорядоченное движение жидкости осуществляется по замкнутому контуру и что давление на выходе насоса незначительно отличается от давления на входе в гидродвигатель. При этом давление нагнетания определяется величиной нагрузки на выходе привода.
Принцип дроссельного регулирования базируется на законе гидравлики, выводится из уравнения Бернулли и обычно записывается в следующем виде
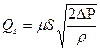
где m= 0,6-0,75 - коэффициент расхода (опытная величина),
S - площадь щели (отверстия),
DР - перепад давлений в полостях до щели и за ней,
r - плотность жидкости 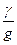 .
.
Приводы с дроссельным регулированием также широко используются в военной технике и особенно в системах управления и автоматики. Эти приводы дешевле (стоимость регулируемого насоса приблизительно в 4-5 раз выше нерегулируемого той же конструктивной схемы). Правда, у них ниже КПД. Характерной особенностью гидроприводов с дроссельным регулированием является наличие разомкнутости в контуре циркуляции жидкости и независимость давления на выходе из насоса от нагрузки на гидродвигатель (Р1 = const - поэтому и КПД ниже при малых нагрузках).
В гидроприводах с комбинированным регулированием используются оба вышеуказанных принципа. На практике они встречаются редко.
Лекция № 16
Особенности гидроприводов и области их применения
В современной технике наиболее широко применяются четыре типа приводов: электрические, механические, гидравлические и пневматические. Все они… Для правильной ориентировки в выборе типа привода для того или иного рабочего… Говоря об особенностях гидравлических приводов в первую очередь необходимо заметить, что они обладают удачным…Лекция № 17
НАСОСЫ И ГИДРАВЛИЧЕСКИЕ ДВИГАТЕЛИ
По конструктивно-кинематическим признакам все существующие ротационно-поршневые насосы и гидромоторы чаще всего…Универсальный регулятор скорости (УРС)
Рис. 8.1 В блоке цилиндров 1 расположены поршни 2. Золотниково-распределительное устройство 3 обеспечивает образование двух…Рис. 8.3
Величина хода поршня, пропорциональна a, и, при прочих равных условиях, определяет количество подаваемой насосом жидкости. Если в процессе вращения вала с одной и той же скоростью и в одну сторону изменять угол a, например, от 20о до 0о, то будет изменяться и количество перекачиваемой жидкости от какого-то значения Q до 0 (естественно a не может быть равен или превышать 45о, обычно a = 15¸30о).
При переходе шайбы через вертикальную ось (ось “мертвых положений”), направление потока жидкости изменится на противоположное, т.е. произойдет реверс потока жидкости и, в итоге, реверс движения выходного вала.
Так эта машина работает в роли насоса. Если же под поршни такой машины, через распределитель, подавать жидкость под давлением от какого-либо источника, то она будет гидродвигателем, в котором энергия потока жидкости будет преобразовываться в механическую энергию и через его вал передаваться управляемому рабочему органу.
То есть ротационно-поршневые машины, как и всякие другие типы гидравлических машин, в принципе обратимы (необратимыми являются машины лишь с клапанным распределением) и в этом плане они аналогичны электрическим машинам постоянного тока.
Поскольку это так, то очевидно гидропривод может быть образован из двух принципиально одинаковых машин, одна из которых регулируема и используется, например, в качестве насоса, вращаясь в одну и ту же сторону с w1 = const, а другая нерегулируема и используется в качестве гидродвигателя (гидромотора), для которого w2 = var.
Именно по такой схеме в 1905 году в Америке, инженером Дженни был изобретен первый высококачественный гидравлический агрегат, предназначенный для передачи механической энергии от какого-либо источника к рабочему органу машины и регулирования скорости движения этого органа.
Этот аппарат, названный вначале “муфтой Дженни”, не был признан на родине создателя. Однако, был сразу же оценен русскими инженерами военно-морского флота, прошедшими Цусимское сражение, в результате которого для русского флота трагическую роль сыграл электропривод на башенных артиллерийских установках.Машина очень хорошо отработана, обладает большой долговечностью и надежностью. Однако, по ряду параметров (частота вращения 500 об/мин), давление 15¸75 кГ/см2) не удовлетворяет требованиям некоторых современных отраслей техники, и в частности требованиям к приводам летательных аппаратов, пусковых и артиллерийских установок, танков, самоходных кранов и т.п. Пониженные скорости и рабочие давления обусловлены кинематическими особенностями машины - одношарнирным (несинхронным) соединением ведущего и ведомого звеньев (вал-блок цилиндров и ведомая шайба-блок цилиндров). Одношарнирное соединение валов, как известно, ведет к неравномерности текущей скорости ведомого звена (шайба), что в свою очередь вызывает дополнительные динамические нагрузки, в первую очередь на штоки поршней, что ведет к ограничению вышеуказанных параметров. Поэтому в дальнейшем были изобретены более совершенные аксиально-поршневые машины.
8.1.1.2 Машины с качающимся блоком цилиндров
В машинах данного типа введено двух шарнирное соединение. При этом, шайба
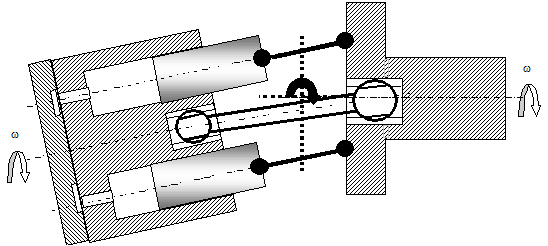
|
названа диском, который располагается перпендикулярно к оси вращения, а блок цилиндров располагается в так называемой “люльке” и может изменять положение в пространстве.
Рис. 8.4
Двух шарнирное (синхронное) соединение ведущего и ведомого звеньев позволило повысить скорость вращения валов до 1000 об/мин для мощных машин и до 10000 об/мин относительно маломощных. Удалось также повысить рабочее давление до 150¸210 кГ/см2 (280¸320 кГ/см2). Габариты и веса гидродвигателей при этом по сравнению с гидродвигателями УРС той же мощности сократились в 10 и более раз. Правда, габариты регулируемого насоса (рис. 8.4) остались практически такими же, ибо для изменения положения в пространстве блока цилиндров в корпусе насоса требуется больший объем, чем для качающейся шайбы. Этот тип машин выпускается серийно во всех развитых странах мира. Причем по сравнению с другими типами объем их выпуска самый большой.
Машина с поворотным диском и косой шайбой
Рис. 8.5Радиально-поршневые машины
В процессе вращения ротора поршень также совершает два движения: переносное и… В основу заложен механизм вращающейся кулисы, который сам по себе образован из кривошипно-шатунного механизма (рис.…Эксцентриковые машины
Ход поршня определяется точно такой же формулой, как и для радиальных машин: h =2e. В принципе в этих машинах можно также найти подобие… Распределение жидкости чаще всего клапанное, хотя есть и с золотниковым… Заключая краткий обзор основных разновидностей ротационно-поршневых машин, отметим, что наиболее распространенными…Список использованной литературы
1. Башта Т.М. Гидравлические приводы летательных аппаратов. М.: Машиностроение, 1967, 495 с.
2. Башта Т.М. Машиностроительная гидравлика. Справочное пособие. М.: Машиностроение, 1971, 671 с.
3. Мелик-Гайказов В.И. и др. Гидропривод тяжелых грузоподъемных машин и самоходных агрегатов. М.: Машиностроение, 1968, 264 с.
4. Дубровский О.Н. и др. Гидравлические приводы судовых механизмов. Л.: Судостроение, 1969, 383 с.
5. Сырицын Т.А. Надежность гидро- и пневмопривода. М.: Машиностроение,
1981, 216 с.
6. Башта Т.М. Объемные насосы и гидравлические двигатели гидросистем. М.: Машиностроение, 1974, 606 с.
7. Кабаков М.Г. Стесин С.П. Технология производства гидроприводов. М.: Машиностроение, 1974, 192 с.
8. Дубровский О.Н. Судовые гидравлические приводы. Л.: Судостроение, 1966, 155 с.
9. Минеев Ю.И. Чернигин Ю.П. Гидравлические системы и приводы судов
на подводных крыльях. Л.: Судостроение, 1972, 176 с.
10. Васильченко В.А. Гидравлическое оборудование мобильных машин. Справочник. М.: Машиностроение, 1983, 301 с.
11. Транспортно - заряжающая машина 2Т6. Техническое описание. Альбом рисунков и схем. Воениздат, 1977.
12. Кран 9Т 35. Альбом рисунков. Техническое описание. Воениздат, 1984
13. Беленков Ю.А. и др. Надежность объемных гидроприводов и их элементов. М.: Машиностроение, 1977, 168 с.
14. Лозовский В.Н. Надежность гидравлических агрегатов. М.: Машиностроение, 1974, 319 с.
– Конец работы –
Используемые теги: Гидросистемы, гидромашины0.04
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Гидросистемы и гидромашины
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?









Новости и инфо для студентов