рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Введение в анализ. Дифференциальное исчисление. Функций одной переменной
Реферат Курсовая Конспект
Введение в анализ. Дифференциальное исчисление. Функций одной переменной
Введение в анализ. Дифференциальное исчисление. Функций одной переменной - раздел Философия, Министерство Образования И Науки Российской Федерации ...
Министерство образования и науки Российской Федерации
Волжский институт строительства и технологий
(филиал) государственного образовательного учреждения
высшего профессионального образования
«Волгоградский государственный архитектурно-строительный университет»
Кафедра высшей математики
Введение в анализ.
Дифференциальное исчисление
Функций одной переменной
Методические указания по самостоятельной работе и
Задания контрольной работы
Для студентов заочной формы обучения
по направлениям «Строительство» и
«Наземные транспортно-технологические комплексы»
Волжский, 2012
УДК 65в631
Введение в анализ. Дифференциальное исчисление функций одной переменной: методические указания по самостоятельной работе и задания контрольной работы для студентов заочной формы обучения по направлениям «Строительство» и «Наземные транспортно-технологические комплексы» / ВИСТех (филиал) ВолгГАСУ ; [сост. Е. В. Абрамов, Е. Д. Илларионова, В. Н. Торопшина]. – Волжский : ВИСТех (филиал) ВолгГАСУ, 2012. – 36 с.
Представлен необходимый теоретический материал и варианты контрольной работы по теме «Введение в анализ. Дифференциальное исчисление функций одной переменной» с примером ее выполнения, а также требования к оформлению контрольных работ, вопросы для самопроверки и список рекомендуемой литературы.
Предназначено для студентов, обучающихся в 1 семестре на заочной форме обучения по направлениям «Строительство» и «Наземные транспортно-технологические комплексы».
Библиогр. 4 Табл. 2 Ил. 6
Содержание
| 1. Методические указания по самостоятельной работе……………… | |
| 2. Требования к оформлению контрольной работы………………….. | |
| 3. Рекомендуемая литература для самостоятельной работы………… | |
| 4. Контрольная работа «Введение в анализ. Дифференциальное исчисление функций одной переменной» | |
| 4.1. Основные теоретические сведения…………………………….. | |
| 4.2. Контрольные задания…………………………………………… | |
| 4.3. Пример решения контрольной работы………………………… | |
| 4.4. Вопросы для самопроверки…………………………………….. | |
| 5. Список литературы ………………………………………………….. |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО САМОСТОЯТЕЛЬНОЙ
РАБОТЕ
Важной формой обучения любого студента является самостоятельная работа, которая состоит из изучения материала по учебникам, решения задач, самопроверки и выполнения контрольных работ. В помощь студенту проводятся лекции, практические и лабораторные занятия. Кроме того, студент может обращаться к преподавателю с вопросами.
Изучение учебника должно проводиться систематически. Переходить к следующему вопросу можно только после правильного понимания предыдущего. Особое внимание надо обращать на определение основных понятий и формулировки основных теорем. Правильному пониманию теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в теоремах. Полезно внимательно разбирать геометрический смысл различных понятий и утверждений. При изучении материала по учебнику полезно вести конспект, на полях которого отмечать вопросы для консультации с преподавателем.
Составление листа, содержащего важнейшие и наиболее часто используемые формулы курса не только помогает их запоминанию, но и дает возможность использовать этот лист как справочник при решении задач.
Чтение учебника должно сопровождаться решением задач, для чего следует завести специальную тетрадь. При решении задач надо обосновывать каждый этап решения, исходя из теоретических положений курса.
Решение задач надо записывать подробно, вычисления располагать в строгом порядке и обязательно выполнять проверку.
Умение решать задачи необходимо для хорошего усвоения теории, но не является доказательством такого усвоения, так как часто при решении задач формулы и утверждения используются чисто механически.
После изучения какой-либо темы следует провести самопроверку, для чего воспроизвести по памяти основные понятия, определения, формулы и формулировки теорем, вспомнить их выводы.
Если в процессе работы у студента возникают вопросы, которые не удается разрешить самостоятельно, то он может обратиться к преподавателю за письменной или устной консультацией.
В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Контрольные работы должны выполняться самостоятельно. Это дает рецензенту возможность указать студенту на недостатки в его работе, в усвоении им учебного материала.
На экзаменах и зачетах выясняется усвоение теоретических и прикладных вопросов программы и умение применять полученные знания к решению задач. При подготовке к экзамену учебный материал рекомендуется повторять по учебнику и конспекту.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ
РАБОТЫ
При выполнении контрольных работ следует придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены и возвращены студенту для доработки.
1. Каждую контрольную работу следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны номер контрольной работы, название дисциплины, фамилия, имя, отчество студента, номер зачетной книжки, номер варианта, специальность и группа, в которой обучается студент. В конце работы следует проставить дату ее выполнения и расписаться.
3. Для студентов заочной формы обучения номер варианта контрольной работы соответствует последней цифре номера зачетной книжки. Если номер зачетной книжки оканчивается цифрой «0», то студент выполняет 10-й вариант. Студенты-дневники получают номер варианта по усмотрению преподавателя.
4. В работу включаются все задачи строго по положенному варианту. Работа, содержащая не все задачи варианта или задачи не своего варианта, не зачитывается.
5. Решения задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Перед решением каждой задачи надо выписать полностью ее условие. Решения задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.
6. Если работа не зачтена или сделаны замечания по решению задач, следует выполнить работу над ошибками в той же тетради. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ДЛЯ
САМОСТОЯТЕЛЬНОЙ РАБОТЫ
2. Данко, П. Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А.. Г. Попов, Т. Я. Кожевников. В 2-х ч. Ч. 1. – 4-е изд., испр. и доп. –… 3. Кудрявцев, В.А. Краткий курс высшей математики / В. А. Кудрявцев, Б. П.… 4. Меркулов, В. А. Курс высшей математики. Избранные разделы : учеб. пособие / В. А. Меркулов. – Волгоград : ВолгГАСУ,…Комплексные числа
Основные понятия
1. Алгебраическая форма комплексного числа:  , где
, где  – действительная часть,
– действительная часть,  – мнимая часть, i – мнимая единица, такая что
– мнимая часть, i – мнимая единица, такая что  .
.
2. Комплексное число  есть противоположное к комплексному числу
есть противоположное к комплексному числу  .
.
3. Комплексное число  есть сопряженное к комплексному числу
есть сопряженное к комплексному числу  .
.
4. Два комплексных числа 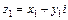 и
и  равны, если x1 = x2 и y1 = y2.
равны, если x1 = x2 и y1 = y2.
5. Сумма (разность) двух комплексных чисел 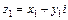 и
и  есть комплексное число
есть комплексное число  .
.
6. Произведение двух комплексных чисел 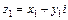 и
и  есть комплексное число
есть комплексное число  .
.
7. Частное двух комплексных чисел 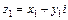 и
и  есть комплексное число
есть комплексное число
 .
.
8.  где
где  – натуральное число.
– натуральное число.
9. Комплексное число  на плоскости можно изобразить точкой
на плоскости можно изобразить точкой  или радиус-вектором
или радиус-вектором  точки
точки  (рис. 1).
(рис. 1).
 |
Рис. 1
10. Модуль комплексного числа  есть действительное число
есть действительное число  (рис. 1).
(рис. 1).
11. Аргумент комплексного числа  есть угол
есть угол  (рис. 1), вычисляемый по формулам:
(рис. 1), вычисляемый по формулам: 
12. Тригонометрическая форма комплексного числа:  .
.
13. Произведение двух комплексных чисел в тригонометрической форме  и
и 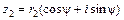 есть комплексное число
есть комплексное число  .
.
14. Частное двух комплексных чисел в тригонометрической форме  и
и 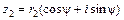 есть комплексное число
есть комплексное число  .
.
15. Степень комплексного числа в тригонометрической форме  есть комплексное число
есть комплексное число  , где
, где  – натуральное число (формула Муавра).
– натуральное число (формула Муавра).
16. Корень натуральной степени n из комплексного числа в тригонометрической форме  есть комплексное число
есть комплексное число  , где
, где  (формула Муавра).
(формула Муавра).
17. Показательная форма комплексного числа:  .
.
18. Произведение двух комплексных чисел в показательной форме  и
и  есть комплексное число
есть комплексное число  .
.
19. Частное двух комплексных чисел в показательной форме  и
и  есть комплексное число
есть комплексное число  .
.
20. Степень комплексного числа в показательной форме  есть комплексное число
есть комплексное число 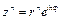 , где
, где  – натуральное число.
– натуральное число.
Элементы теории пределов
Основные понятия
1. Постоянное число a называется пределом переменной x, если для любого сколь угодно малого числа d > 0 можно указать такое значение х, что все последующие значения будут удовлетворять неравенству
|x – a| < d. Обозначение: lim x = a или x ® a.
Неравенство |x – a| < d перепишем в виде –d < x – a < d или
a – d < x < a + d. Интервал (a – d; a + d) называется окрестностью точки x = a радиуса d.
2. Постоянное число l называется пределом функции y = f(x) при x ® a, если для всех значений х, достаточно близких к а, значение f(x) сколь угодно мало отличается от l. Обозначение:  или
или 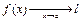 . (1)
. (1)
Определение включает так же случаи, когда числа а и l будут заменены символами «¥», «–¥», «+¥».
В определении не требуется, чтобы функция y = f(x) была определена в самой точке x = a.
3. Если существует предел (1) и x < a, то его называют пределом слева и обозначают  . (2) Аналогично, если существует предел (1) и x > a, то его называют пределом справа и обозначают
. (2) Аналогично, если существует предел (1) и x > a, то его называют пределом справа и обозначают 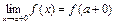 . (3)
. (3)
Пределы (2) и (3) называются односторонними пределами.
Если a = 0, то вместо x ® 0 – 0 и x ® 0 + 0 пишут соответственно x ® –0 и x ® +0.
4. Связь односторонних пределов с пределом (1) выражается следующей теоремой: для того, чтобы существовал предел (1) необходимо и достаточно, чтобы выполнялось равенство f(a – 0) = f(a + 0).
5. Пусть функция y = f(x) определена в некоторой окрестности точки x = х0, кроме, быть может, самой точки х0. Функция y = f(x) называется бесконечно малой при x ® х0, если  и называется бесконечно большой при x ® х0, если
и называется бесконечно большой при x ® х0, если  .
.
Здесь и в дальнейшем под символом х0 подразумевается либо точка а либо ¥. Аналогично определяются бесконечно малые и бесконечно большие функции в случае односторонних пределов.
6. Если a(x) – бесконечно малая функция при x ® х0 и a(x) ¹ 0 при x ¹ х0, то обратная величина  есть бесконечно большая функция при x ® х0. И наоборот, если a(x) – бесконечно большая, то
есть бесконечно большая функция при x ® х0. И наоборот, если a(x) – бесконечно большая, то  – бесконечно малая функция.
– бесконечно малая функция.
При решении задач удобно пользоваться следующей символической записью. Пусть число a > 0, тогда  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Основные теоремы о действиях над функциями, имеющими конечный предел
8. . 9. при . 10. , где C = const.Виды неопределенностей
16. Если и , то разность f(x) – g(x) при x → х0 называется неопределенностью вида (¥ – ¥), а частное при x → х0 называется… 17. Если и , то произведение f(x) × g(x) при x → х0 называется… Существуют и другие виды неопределенностей.Замечательные пределы
19. Некоторые следствия из первого замечательного предела: 1) ; 2) ; 3) ; 4) ;Непрерывность функции в точке. Точки разрыва
1) существует ; 2) существует f(a); 3) .Дифференциальное исчисление функций одной переменной
Основные понятия
1. Пусть функция  определена на интервале (a; b). Производной функции
определена на интервале (a; b). Производной функции  в точке x0 называется предел отношения приращения функции Df(x0) = f(x0 + Dx) – f(x0) в точке x0 к приращению аргумента Dx, когда
в точке x0 называется предел отношения приращения функции Df(x0) = f(x0 + Dx) – f(x0) в точке x0 к приращению аргумента Dx, когда  , т. е.
, т. е.  .
.
2. Производная от функции  в точке
в точке  имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции
имеет геометрический смысл углового коэффициента касательной, проведенной к графику функции  в точке
в точке  (рис. 2).
(рис. 2).

Рис. 2
Уравнение касательной:  .
.
Уравнение нормали:  .
.
3. Производная от пути по времени при прямолинейном движении материальной точки по закону S = S(t) имеет механический смысл мгновенной скорости в момент времени t = t0, т. е.  .
.
4. Выражение  называется дифференциалом функции y = f(x) в точке x = x0 и обозначается символом
называется дифференциалом функции y = f(x) в точке x = x0 и обозначается символом  , где по определению обозначено dx = Dx.
, где по определению обозначено dx = Dx.
Дифференциал в произвольной точке х равен:  .
.
5. Дифференциал функции y = f(x) имеет геометрический смысл части приращения функции в точке х0 при перемещении не по графику функции, а по графику касательной, проведенной в точке (х0; f(x0)) (рис. 2).
Таблица производных
6.  . 7.
. 7.  , a – любое.
, a – любое.
8.  . 9.
. 9.  .
.
10.  . 11.
. 11.  .
.
12.  . 13.
. 13.  .
.
14.  . 15.
. 15.  .
.
16.  . 17.
. 17.  .
.
18.  . 19.
. 19.  .
.
Основные правила дифференцирования
22. , C = const. 23. . 24. Дифференцирование сложной функции: пусть сложная функция y = f(j(x))… .Производные и дифференциалы высших порядков
28. Производная второго порядка от пути по времени при прямолинейном неравномерном движении материальной точки по закону S = S(t) имеет механический… 29. Производная второго порядка от функции, заданной параметрически находится… 30. Для нахождения производной второго порядка функции, заданной неявно нужно сначала найти первую производную (см. п.…Применения производной
33. Если функция непрерывна в точке и при переходе через точку первая производная меняет знак с «+» на «–», то в точке функция имеет максимум; если… 34. График дифференцируемой на интервале (a; b) функции y = f(x) называется… Если на некотором промежутке , то на этом промежутке функция вогнута; если , то функция выпукла.Рис. 3
36. Для нахождения наибольшего или наименьшего значения функции  на отрезке
на отрезке 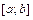 нужно:
нужно:
1) найти критические точки – точки, в которых производная функции  , не существует или равна бесконечности;
, не существует или равна бесконечности;
2) найти значения функции в критических точках, принадлежащие отрезку 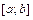 и на концах отрезка;
и на концах отрезка;
3) выбрать среди полученных чисел наибольшее или наименьшее.
37. Для исследования функции  и построения ее графика пользуются следующей схемой:
и построения ее графика пользуются следующей схемой:
1) определить область определения функции, найти точки разрыва;
2) проверить четность, нечетность, периодичность графика;
3) определить наличие вертикальных, горизонтальных и наклонных асимптот;
4) найти производную  , определить интервалы возрастания
, определить интервалы возрастания  , убывания
, убывания  и критические точки (
и критические точки ( или не существует) функции, найти экстремумы;
или не существует) функции, найти экстремумы;
5) найти вторую производную  , определить интервалы выпуклости вверх
, определить интервалы выпуклости вверх  , выпуклости вниз
, выпуклости вниз 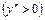 и точки перегиба графика;
и точки перегиба графика;
6) если необходимо, найти дополнительные точки;
7) используя всю полученную информацию, строят график функции  .
.
Вектор-функция скалярного аргумента
Основные понятия
1. Пусть дан радиус-вектор  , концом которого является точка A(x; y; z). Выражая этот вектор через проекции на оси координат, получим
, концом которого является точка A(x; y; z). Выражая этот вектор через проекции на оси координат, получим
 . (1)
. (1)
Пусть проекции вектора  есть функции некоторого параметра t:
есть функции некоторого параметра t:
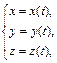 (2)
(2)
тогда формула (1) примет вид
 или коротко
или коротко  . (3)
. (3)
При изменении t изменяются x, y, z – координаты точки А и, следовательно, изменяется вектор  по величине и по направлению, поэтому вектор
по величине и по направлению, поэтому вектор  называют вектор-функцией скалярного аргумента t.
называют вектор-функцией скалярного аргумента t.
Линию в пространстве, которую описывает точка А – конец вектора  называют годографом этого вектора. Уравнения (2) называются параметрическими уравнениями линии в пространстве, а уравнение (3) – векторным уравнением линии в пространстве.
называют годографом этого вектора. Уравнения (2) называются параметрическими уравнениями линии в пространстве, а уравнение (3) – векторным уравнением линии в пространстве.
2. Пусть 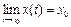 ,
,  ,
,  , тогда говорят, что вектор
, тогда говорят, что вектор  есть предел вектора
есть предел вектора  , и пишут
, и пишут
 . (4)
. (4)
3. Производной вектор-функции  по скалярному аргументу t называют предел отношения приращения вектор-функции
по скалярному аргументу t называют предел отношения приращения вектор-функции  к приращению Dt скалярного аргумента t, т. е.
к приращению Dt скалярного аргумента t, т. е.
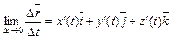 (5)
(5)
и обозначают символом  или
или  .
.
Таким образом, по определению
 . (6)
. (6)
4. Производная вектор-функции  является новой вектор-функцией и называется производной первого порядка. Производная от производной
является новой вектор-функцией и называется производной первого порядка. Производная от производной  называется производной второго порядка и обозначается
называется производной второго порядка и обозначается  или
или  , т. е.
, т. е.
 . (7)
. (7)
Аналогично определяются производные вектор-функций более высоких порядков. Производные вектор-функций порядка старше первого называются производными высших порядков.
5. Касательная к пространственной кривой определяется так же как и в случае плоской кривой. Так как производная  – это вектор, направленный по касательной к пространственной кривой в точке касания M(x(t0); y(t0); z(t0)), то уравнения касательной к кривой
– это вектор, направленный по касательной к пространственной кривой в точке касания M(x(t0); y(t0); z(t0)), то уравнения касательной к кривой  в этой точке (при t = t0) имеют вид:
в этой точке (при t = t0) имеют вид:
 . (8)
. (8)
6. Так же как и в случае плоской кривой, прямая, перпендикулярная к касательной и проходящая через точку касания, называется нормалью к пространственной кривой в данной точке. Нормалей к данной пространственной кривой в данной точке можно провести бесчисленное множество. Все они лежат в плоскости, перпендикулярной к касательной прямой. Эта плоскость называется нормальной плоскостью. Уравнение нормальной плоскости к кривой  в точке t = t0 имеет вид:
в точке t = t0 имеет вид:
 . (9)
. (9)
7. Пусть дана кривая, которая не пересекает саму себя и имеет касательную в каждой своей точке. Проведем две касательные к кривой в некоторых точках А и В и обозначим через j угол поворота касательной при переходе от точки А к точке В (рис. 4). Этот угол называется углом смежности дуги АВ. У двух дуг, имеющих одинаковую длину, больше изогнута та дуга, у которой угол смежности больше. С другой стороны, степень искривленности дуг различной длины не характеризуется только соответствующим углом смежности. Для этого используют кривизну линии, которая характеризует форму кривой, степень ее искривленности, изогнутости.
 |
Рис. 4
Кривизной пространственной кривой в точке А называется предел отношения угла смежности j к длине дуги АВ = Ds, когда длина этой дуги стремится к нулю (когда точка В приближается к точке А), т. е.
 , (10)
, (10)
где величина R, обратная кривизне линии в данной точке, называется радиусом кривизны в этой точке.
Кривизна пространственной линии  в точке t = t0 определяется по формуле:
в точке t = t0 определяется по формуле:
 , (11)
, (11)
где  ,
,  .
.
4.2. Контрольные задания
1. Дано комплексное число z. Требуется:
1) записать число z в алгебраической и тригонометрической формах;
2) найти  .
.
1.  . 2.
. 2.  . 3.
. 3.  .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  .
.
2. Найти пределы функций, не пользуясь правилом Лопиталя.
1. 1)  при: а)
при: а)  ; б)
; б) 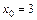 ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
2. 1)  при: а)
при: а)  ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
3. 1)  при: а)
при: а) 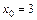 ; б)
; б)  ; в)
; в)  ;
;
2) 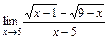 ; 3)
; 3)  .
.
4. 1)  при: а)
при: а)  ; б)
; б) 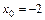 ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
5. 1)  при: а)
при: а)  ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
6. 1)  при: а)
при: а)  ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3) 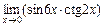 .
.
7. 1) 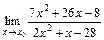 при: а)
при: а)  ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
8. 1)  при: а)
при: а)  ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
9. 1)  при: а)
при: а) 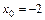 ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
10. 1)  при: а)
при: а) 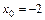 ; б)
; б)  ; в)
; в)  ;
;
2)  ; 3)
; 3)  .
.
3. Задана функция y = f(x). Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
1.  . 2.
. 2.  . 3.
. 3.  .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10. 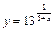 .
.
4. Найти производные  заданных функций.
заданных функций.
1. 1)  ; 2)
; 2)  ;
;
3)  .
.
2. 1)  ; 2)
; 2)  ;
;
3)  .
.
3. 1)  ; 2)
; 2)  ;
;
3)  .
.
4. 1)  ; 2)
; 2)  ;
;
3)  .
.
5. 1)  ; 2)
; 2)  ;
;
3)  .
.
6. 1)  ; 2)
; 2)  ;
;
3)  .
.
7. 1)  ; 2)
; 2)  ;
;
3)  .
.
8. 1)  ; 2)
; 2)  ;
;
3)  .
.
9. 1)  ; 2)
; 2)  ;
;
3)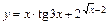 .
.
10. 1)  ; 2)
; 2)  ;
;
3)  .
.
5. Найти производные  и
и  функции, заданной параметрически.
функции, заданной параметрически.
1.  2.
2.  3.
3. 
4.  5.
5. 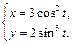 6.
6. 
7.  8.
8.  9.
9. 
10. 
6. Провести полное исследование функции и построить ее график.
1.  . 2.
. 2.  . 3.
. 3.  .
.
4.  . 5.
. 5.  . 6.
. 6.  .
.
7.  . 8.
. 8.  . 9.
. 9.  .
.
10.  .
.
7. Найти уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии  в точке t0.
в точке t0.
1.  ,
,  .
.
2.  ,
,  .
.
3.  ,
,  .
.
4.  ,
,  .
.
5.  ,
,  .
.
6.  ,
,  .
.
7.  ,
,  .
.
8. 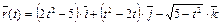 ,
,  .
.
9.  ,
,  .
.
10. 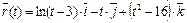 ,
,  .
.
4.3. Пример решения контрольной работы
Задание 1. Дано комплексное число  . Требуется:
. Требуется:
1) записать число z в алгебраической и тригонометрической формах;
2) найти  .
.
Решение. 1) Для записи комплексного числа  в алгебраической форме z = x + yi умножим числитель и знаменатель дроби на выражение 1 + i, сопряженное знаменателю и упростим:
в алгебраической форме z = x + yi умножим числитель и знаменатель дроби на выражение 1 + i, сопряженное знаменателю и упростим:

 .
.
Для записи числа  в тригонометрической форме z = r(cos j+sin j×i) найдем r и j:
в тригонометрической форме z = r(cos j+sin j×i) найдем r и j:
 ,
,
 .
.
Следовательно, получим  .
.
2) Воспользуемся формулой Муавра:
 , где k = 0, 1, 2, …, n – 1.
, где k = 0, 1, 2, …, n – 1.
Полагая k = 0, 1, 2, получим:

 ;
;
 ;
;

 .
.
Это означает, что число  имеет три различных значения.
имеет три различных значения.
Ответ: 1)  – алгебраическая форма комплексного числа,
– алгебраическая форма комплексного числа, 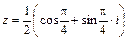 – тригонометрическая форма комплексного числа; 2)
– тригонометрическая форма комплексного числа; 2)  ,
,  ,
,
 .
.
Задание 2. Найти пределы функций, не пользуясь правилом Лопиталя.
1) 
2) 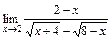 ; 3)
; 3)  .
.
Решение. 1) Данный предел в зависимости от значений  вычисляется разными способами.
вычисляется разными способами.
а)  . Найдем значения функций, стоящих в числителе и в знаменателе дроби,
. Найдем значения функций, стоящих в числителе и в знаменателе дроби, 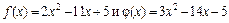 в точке
в точке  :
: 
 . Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:
. Так как полученные значения конечны и отличны от нуля, то по теореме о пределе частного, учитывая непрерывность функций, предел равен значению частного в предельной точке:  ;
;
б)  . Найдем новые значения
. Найдем новые значения  и
и 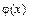 в точке
в точке  :
: 
 . Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке
. Так как числитель и знаменатель дроби оба равны нулю, то заданное отношение в точке  является неопределенностью вида
является неопределенностью вида  и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель
и применять теорему о пределе частного нельзя. Для нахождения предела в этом случае выделим в числителе и знаменателе критический множитель  , создающий неопределенность вида
, создающий неопределенность вида  при
при  . С этой целью найдем корни уравнений
. С этой целью найдем корни уравнений  и
и  , затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель
, затем разложим квадратные трехчлены на линейные множители и после сокращения дроби на общий критический множитель  найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):
найдем предел оставшегося выражения, применяя теорему о пределе частного как в случае пункта а):


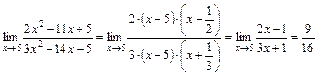 ;
;
в)  . При
. При 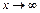 имеем
имеем  и
и  , т. е. заданное отношение при
, т. е. заданное отношение при 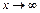 является неопределенностью вида
является неопределенностью вида  и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной
и теорему о пределе частного применять нельзя. Для нахождения в этом случае предела дроби опять выделим в числителе и знаменателе критический множитель, который представляет собой старшую степень переменной  . В данном случае это есть
. В данном случае это есть 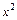 . После сокращения дроби на критический множитель
. После сокращения дроби на критический множитель 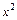 применим теорему о пределе частного и следующие равенства, известные из теории пределов:
применим теорему о пределе частного и следующие равенства, известные из теории пределов:  ,
, 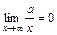 ,
, 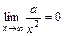 .
.
Получим:
 .
.
2) Найдем значения функций  и
и  , стоящих в числителе и знаменателе дроби, в точке
, стоящих в числителе и знаменателе дроби, в точке 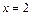 :
:  ,
,  . Следовательно, заданное отношение
. Следовательно, заданное отношение  при
при  является неопределенностью вида
является неопределенностью вида  . Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель
. Для нахождения предела отношения выделим в числителе и в знаменателе критический множитель  , создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю
, создающий неопределенность, и сократим на него дробь. С этой целью умножим числитель и знаменатель на выражение сопряженное знаменателю  и используем формулу сокращенного умножения разности квадратов:
и используем формулу сокращенного умножения разности квадратов:  :
:
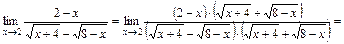


 .
.
По теореме о пределе корня  , получим:
, получим:
 .
.
3)  . Найдем значения функций
. Найдем значения функций  и
и  в точке
в точке  :
:  и
и  . Следовательно, заданное отношение представляет собой при
. Следовательно, заданное отношение представляет собой при 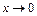 неопределенность вида
неопределенность вида  . Вычислим этот предел, применяя формулу первого замечательного предела:
. Вычислим этот предел, применяя формулу первого замечательного предела:  и равенство
и равенство  , вытекающее из непрерывности в точке
, вытекающее из непрерывности в точке  функции
функции  . С этой целью преобразуем заданный предел следующим образом:
. С этой целью преобразуем заданный предел следующим образом:

 .
.
Ответ: 1), а)  ; б)
; б)  ; в)
; в)  . 2)
. 2)  . 3) 3.
. 3) 3.
Задание 3. Задана функция  . Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
. Построить схематически график функции, вычислив пределы слева и справа в точке разрыва и предел на бесконечности.
Решение. Рассмотрим точку х = 1. Найдем пределы слева и справа функции в данной точке:
 ,
,
 .
.
Так как предел справа равен бесконечности, то х = 1 – точка разрыва второго рода.
Предел функции на бесконечности равен:
 .
.
Строим схематически график функции  , используя полученные результаты (рис. 5).
, используя полученные результаты (рис. 5).

Рис. 5
Задание 4. Найти производные  заданных функций.
заданных функций.
1)  ; 2)
; 2)  ;
;
3) 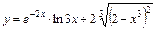 .
.
Решение. 1)  .
.
Используем правило дифференцирование суммы  и правила дифференцирования сложной функции вида
и правила дифференцирования сложной функции вида  , где
, где  , а также таблицу производных. Получим:
, а также таблицу производных. Получим:


 .
.
2) 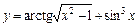 .
.
Используем правило дифференцирование суммы  и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
 ,
,
где  , а также таблицу производных. Получим:
, а также таблицу производных. Получим:

 .
.
3) 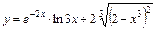 .
.
Используем правило дифференцирования суммы  , правило дифференцирования произведения
, правило дифференцирования произведения  и правила дифференцирования сложных функций вида
и правила дифференцирования сложных функций вида
 ,
,
где  , а также таблицу производных. Получим:
, а также таблицу производных. Получим:


 .
.
Ответ: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Задание 5. Найти производные  и
и  функции
функции  заданной параметрически.
заданной параметрически.
Решение. Производная  функции
функции  , заданной параметрически, вычисляется по формуле:
, заданной параметрически, вычисляется по формуле:
 .
.
Вторую производную найдем по формуле:
 .
.
Ответ:  ,
,  .
.
Задание 6. Провести полное исследование функции  и построить ее график.
и построить ее график.
Решение. 1) Найдем область определения, интервалы непрерывности и точки разрыва функции.
Функция определена на всей числовой оси, кроме точки  , т. е.
, т. е.  . В каждой точке области определения функция непрерывна. Точка
. В каждой точке области определения функция непрерывна. Точка  есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
есть точка разрыва функции, т. к. знаменатель функции в этой точке равен нулю, а числитель отличен от нуля.
2) Выясним четность, нечетность и периодичность функции.
 , т. е.
, т. е.  . Следовательно, функция не является ни четной, ни нечетной.
. Следовательно, функция не является ни четной, ни нечетной.
Функция непериодична, т. к. 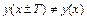 , где Т – некоторое действительное число.
, где Т – некоторое действительное число.
3) Найдем асимптоты графика функции (вертикальные, горизонтальные и наклонные):
|
Так как точка  оси Ox есть точка разрыва функции, то прямая линия
оси Ox есть точка разрыва функции, то прямая линия  , перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки
, перпендикулярная оси Ox, есть вертикальная асимптота графика. Исследуем поведение графика функции вблизи вертикальной асимптоты по односторонним пределам функции. Возьмем слева от точки  близкое значение, например,
близкое значение, например,  и вычислим в нем значение функции и ее знак:
и вычислим в нем значение функции и ее знак:
 .
.
Так как это значение отрицательно, и функция слева от точки  непрерывна, то она сохраняет знак и
непрерывна, то она сохраняет знак и  .
.
Теперь возьмем справа от точки  близкое значение, например,
близкое значение, например,  :
:
 .
.
Так как это значение положительно, и функция справа от точки  непрерывна, то при переходе к пределу функция сохраняет знак и
непрерывна, то при переходе к пределу функция сохраняет знак и  .
.
Таким образом, слева от точки  функция отрицательна, а справа от точки
функция отрицательна, а справа от точки  – положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции);
– положительна и имеет односторонние пределы, равные бесконечности. Такая точка называется точкой разрыва второго рода (или точкой бесконечного разрыва функции);
б) Горизонтальные асимптоты.
Для нахождения горизонтальной асимптоты нужно найти предел функции при 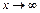 , раскрывая неопределенность вида
, раскрывая неопределенность вида  . Если существует конечный предел
. Если существует конечный предел  , то прямая, определяемая уравнением
, то прямая, определяемая уравнением  , есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
, есть горизонтальная асимптота графика. Если же этот предел равен бесконечности, то горизонтальной асимптоты нет. Найдем предел:
 .
.
Предел равен бесконечности, значит горизонтальной асимптоты нет;
в) Наклонные асимптоты.
Наклонная асимптота имеет уравнение прямой линии с угловым коэффициентом вида  , где
, где  ,
,  . Если
. Если  , то наклонной асимптоты не существует.
, то наклонной асимптоты не существует.
Найдем оба указанных предела для заданной функции:
 ,
,
 .
.
Таким образом, график имеет наклонную асимптоту 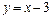 .
.
4) Найдем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции.
Находим сначала первую производную функции:

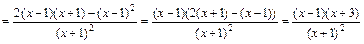 .
.
Так как точка  , в которой
, в которой  не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых
не существует, не принадлежит области определения функции, то критическими точками первого рода являются лишь точки, в которых  или
или  , т. е.
, т. е.  .
.
Критические точки и точка разрыва  разбивают ось Ox на 4 интервала монотонности функции. По знаку производной
разбивают ось Ox на 4 интервала монотонности функции. По знаку производной  в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
в этих интервалах определяем интервалы возрастания и убывания функции, точки экстремума и экстремумы функции. Полученные данные заносим в табл. 1.
Таблица 1

| 
| 
| 
| 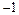
| 
| 
| |

| + | – | не сущ. | – | + | ||

| ä | –8 max | æ | не сущ. | æ | min | ä |
5) Найдем интервалы выпуклости и вогнутости графика функции, точки перегиба.
Находим сначала вторую производную функции:


 .
.
Так как точка не принадлежит области определения функции и
не принадлежит области определения функции и  , то критических точек второго рода нет.
, то критических точек второго рода нет.
Точка разрыва разбивают числовую ось Ox на 2 интервала, в которых по знаку второй производной  определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
определяем интервалы выпуклости и вогнутости графика. Полученные данные заносим в табл. 2.
Таблица 2

| 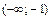
| 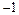
| 
|

| – | не сущ. | + |

| Ç выпуклый | не сущ. | È вогнутый |
6) Находим точки пересечения графика функции с осями координат, решая две системы уравнений.
С осью Ox: 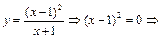 А(1; 0) – точка пересечения графика с осью Ox.
А(1; 0) – точка пересечения графика с осью Ox.
С осью Oy:  В(0; 1) – точка пересечения графика с осью Oу.
В(0; 1) – точка пересечения графика с осью Oу.
7) Используя результаты исследования, строим график функции в такой последовательности: а) строим вертикальную асимптоту  и наклонную асимптоту
и наклонную асимптоту 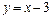 , подписываем их; б) изображаем максимум функции в точке
, подписываем их; б) изображаем максимум функции в точке  и минимум в точке
и минимум в точке  ; в) наносим на осях точки А(1; 0) и В(0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот (рис. 6).
; в) наносим на осях точки А(1; 0) и В(0; 1) пересечения графика с осями координат; г) нанесенные на плоскость точки соединяем гладкими линиями с учетом табл. 1 и 2 и поведения функции вблизи асимптот (рис. 6).
Задание 7. Найти уравнения касательной, уравнение нормальной плоскости и вычислить кривизну линии  в точке t0 = 1.
в точке t0 = 1.
Решение. 1)Для составления уравнений касательной в точке t0 = 1 воспользуемся формулой  . Имеем:
. Имеем:
 ,
,  ,
, 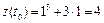 ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  .
.
Таким образом, получим:  .
.
 |
Рис. 6
2) Запишем уравнение нормальной плоскости в точке t0 = 1 по формуле  и упростим:
и упростим:
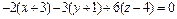 или
или  или
или  .
.
3) Для нахождения кривизны линии в точке t0 = 1 применим формулу  , где
, где  ,
,  . Имеем:
. Имеем:
 ;
;
 ;
;
 ,
,
 ;
;

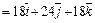 ,
,
 .
.
Таким образом, окончательно получим:  .
.
Ответ: 1)  – уравнения касательной в точке t0 = 1; 2)
– уравнения касательной в точке t0 = 1; 2)  – уравнение нормальной плоскости в точке t0 = 1.
– уравнение нормальной плоскости в точке t0 = 1.
4.4. Вопросы для самопроверки
1. Основные понятия о комплексных числах. Геометрическое изображение комплексного числа. Тригонометрическая и показательная формы записи комплексных чисел.
2. Действия над комплексными числами в алгебраической форме.
3. Действия над комплексными числами в тригонометрической форме. Формулы Муавра.
4. Действия над комплексными числами в показательной форме.
5. Предел переменной. Окрестность точки. Предел функции в точке и на бесконечности. Односторонние пределы.
6. Бесконечно малые и бесконечно большие функции, ограниченные функции. Их свойства.
7. Основные теоремы о пределах функций. Неопределенности.
8. Теорема о сжатой функции. Первый замечательный предел.
9. Основные понятия о числовых последовательностях.
10. Число е. Второй замечательный предел.
11. Непрерывность функции в точке. Точки разрыва. Свойства непрерывных функций.
12. Свойства функций непрерывных на отрезке.
13. Определение производной функции в точке и на интервале.
14. Геометрический и механический смысл производной.
15. Дифференцируемость и непрерывность функций. Дифференциал функции.
16. Формулы и правила дифференцирования функций.
17. Дифференцирование сложной функции, неявной функции и функции, заданной параметрически.
18. Производные и дифференциалы высших порядков.
19. Экстремум функции. Необходимые и достаточные условия экстремума.
20. Выпуклость и вогнутость графика функции. Точки перегиба.
21. Асимптоты графика функции.
22. Наибольшее и наименьшее значения функции на отрезке.
23. Полное исследование функции и построение ее графика.
24. Понятие вектор-функции скалярного аргумента.
25. Как определяется предел и производная вектор-функции скалярного аргумента?
26. Понятие кривизны плоской линии. Формула для ее вычисления.
27. Касательная и нормальная плоскость пространственной линии в точке. Их уравнения.
Список литературы
1. Лунгу, К. Н. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу [и др.]. – М.: Рольф, 2001. – 576 с.
2. Методические указания для студентов специальности 060800 «Экономика и управление на предприятии (строительство)» заочной формы обучения по дисциплине «Высшая математика» / ВИСТех (филиал) ВолгГАСУ; [сост. Е.В. Абрамов, Е.Д. Илларионова, Е.Ю. Волченко]. – Волжский: ВИСТех (филиал) ВолгГАСУ, 2010. – 95 с.
3. Письменный, Д. Т. Конспект лекций по высшей математике. 1 часть. / Д. Т. Письменный. – М.: Рольф, 2001. – 288 с.
4. Рябушко, А. П. Сборник индивидуальных заданий по высшей математике. Часть 1 / А. П. Рябушко [и др.]. – Мн.: Выш. шк., 1992
План уч.-метод. докум. 2012 г., поз. № 20
Составители: Е.В. Абрамов, Е.Д. Илларионова, В.Н. Торопшина
Введение в анализ.
Дифференциальное исчисление
функций одной переменной
Методические указания по самостоятельной работе и
задания контрольной работы
для студентов заочной формы обучения
по направлениям «Строительство» и
«Наземные транспортно-технологические комплексы»
Редактор Е. В. Румянцева
Подписано в печать 19.05.2010 г. Формат 60 х 84 / 16.
Гарнитура Times New Roman. Бумага UNION PRINTS.
Печать трафаретная.
Усл. печ. л. 5,52. Уч.-изд. л. 5,94. Т. 62 экз.
Волжский институт строительства и технологий (филиал)
Волгоградского государственного архитектурно-строительного университета
404111 г. Волжский, пр. Ленина, 72
– Конец работы –
Используемые теги: Введение, анализ, ДИФФЕРЕНЦИАЛЬНОЕ, исчисление, функций, одной, переменной0.086
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Введение в анализ. Дифференциальное исчисление. Функций одной переменной
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?








Новости и инфо для студентов