Методы линейного программирования, двойственность в линейном программировании

СОДЕРЖАНИЕ

 

1. Методы линейного программирования, двойственность в линейном программировании 3

Задание 2. 10

Задание 3. 17

Задание 4. 19

Задание 5. 25

Список использованных источников. 28

 

Методы линейного программирования, двойственность в линейном программировании

Методы и модели линейного программирования широко применяются при оптимизации процессов во всех отраслях народного хозяйства: при разработке… Особенностью задач линейного программирования является то, что экстремума… Форма записи задачи линейного программирования выглядит следующим образом.

Задание 2

Фирма выпускает два вида комплексных удобрений для газонов в упаковке – обычное и улучшенное. Обычное удобрение стоит 3 дн. ед./уп. и включает 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений. Улучшенное удобрение стоит 4 ден. ед./уп. и включает 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений.

Для подкормки некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений.

Определите, сколько и каких удобрений нужно купить, чтобы обеспечить эффективное питание растений и минимизировать стоимость покупки.

Постройте экономико-математическую модель задачи, дайте необходимые комментарии к ее элементам и получите решение графическим методом. Что произойдет, если решать задачу на максимум, и почему.

Осуществите проверку правильности решения с помощью средств MS Excel (надстройка Поиск решения).

 

Решение.

Обозначим через х₁ и х₂, соответственно, количество обычных и улучшенных наборов удобрений.

Составим целевую функцию и систему ограничений.

min

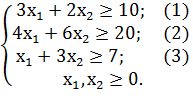
Прямые ограничения означают, что область решений будет лежать в первой четверти декартовой системы координат. По ограничениям строим область всех допустимых решений.

Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением уравнения служат точки прямой 3х₁ + 2х₂ –10 = 0. Построим прямую по двум точкам: (0; 5) и (2; 2). На рис. 2.1 обозначим ее цифрой I.

Определим множество решений второго неравенства. Построим линию по точкам: (5;0) и (2;2). На рис. 2.1 обозначим ее цифрой II.

Определим множество решений третьего неравенства. Построим линию по точкам: (7;0) и (1;2). На рис. 2.1 обозначим ее цифрой III.

Пересечением всех плоскостей является неограниченная область ABCDEF (рис. 2.1).

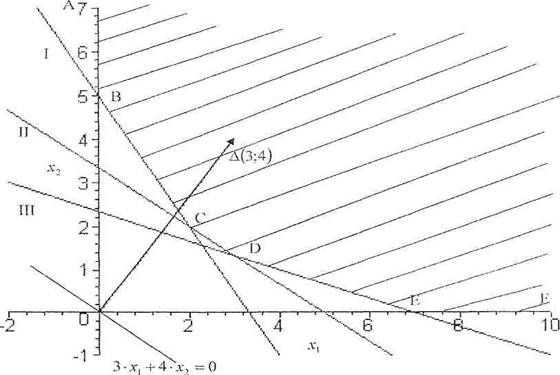
Рис. 2.1. Графическое решение задачи

 

Для определения направления движения к оптимуму построим вектор-градиент, соединив его вершину ∆(3;4) с началом координат.

Построим линию уровня 3x + 4y = 0 по точкам: (0;0) и (4;-3). Эта линия будет перпендикулярна вектору-градиенту.

При минимизации целевой функции необходимо перемещать линию уровня в направлении, противоположном вектору-градиенту. В данном примере, первое касание прямой области допустимых решений произойдет в точке С (2;2). В точке С значение функции будет наименьшим:

f(min) = f(2;2) = 3 * 2 + 4 * 2 = 14 ден. ед.

Таким образом, чтобы минимизировать стоимость удобрений, необходимо купить 2 обычных набора удобрений и 2 улучшенных набора удобрений. При этом минимальные затраты на покупку удобрений составят 14 ден. ед.

Построенная область допустимых решений не ограничена сверху, следовательно, если задачу решать на максимум, то f(max) = ∞, т.е. не имеет конечного оптимума, так как область допустимых значений не ограничена сверху.

Проведем проверку правильности решения задачи с помощью средств MS Excel (надстройка Поиск решения).

Подготовим форму и введем в нее данные (рис. 2.2).

Рис. 2.2. Исходные данные

 

Введем зависимость для целевой функции (ЦФ) с помощью математической функции СУММПРОИЗВ(). В строке «Массив1» вводим C3:D3; в строке «Массив 2» – С4:D4. Нажимаем ОК (рис. 2.3).

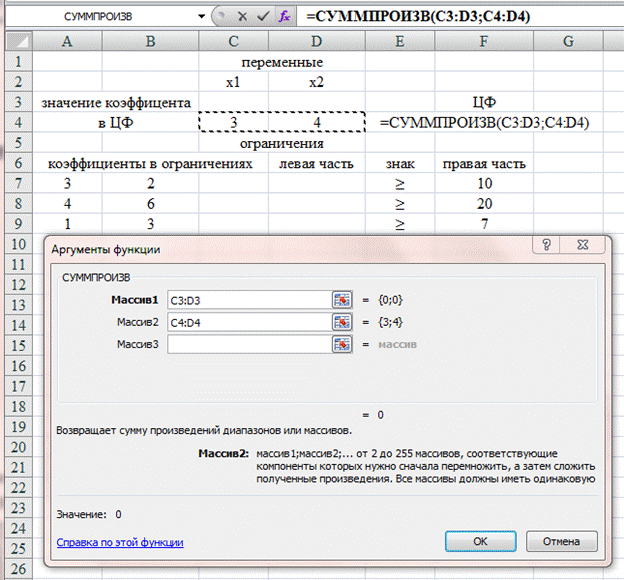
Рис. 2.3. Зависимость для целевой функции

 

Далее аналогично введем с помощью математической функции СУММАПРОИЗВ() зависимости для всех ограничений:

- строка «Массив 1» - С3:D3; строка «Массив 2» - А7:В7;

- строка «Массив 1» - С3:D3; строка «Массив 2» - А8:В8;

- строка «Массив 1» - С3:D3; строка «Массив 2» - А:В9.

Далее для решения воспользуемся надстройкой Поиск решения.

Курсор в поле «Установить целевую ячейку», вводим адрес $F$4, вводим направление целевой функции – «минимальному значению».

Вводим адрес искомых переменных: курсор в поле «Изменяя ячейки», вводим адреса $C$3:$D$3.

Далее вводим ограничения. Курсор в поле «Добавить». В поле «Ссылка на ячейку» вводим адрес $D$7; знак ограничения «>=»; курсор в поле «Ограничение», вводится $F$7$, нажимаем «Добавить». Далее вводим второе и третье ограничение. Нажимаем «ОК».

На экране появится диалоговое окно «Поиск решения» с введенными условиями (риc. 2.4).

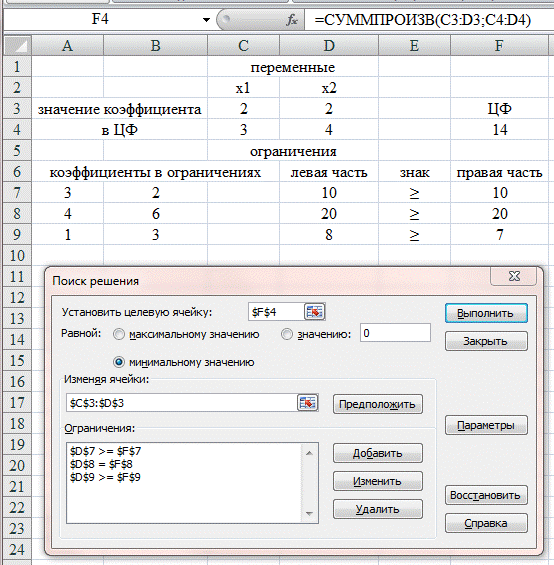
Рис. 2.4. Условия для решения задачи

 

Далее нажимаем «Параметры» в окне «Поиск решения».

Устанавливаем флажок на «Линейная модель», что обеспечивает применение симплекс-метода. Устанавливаем флажок на «Неотрицательные значения» (рис. 2.5).

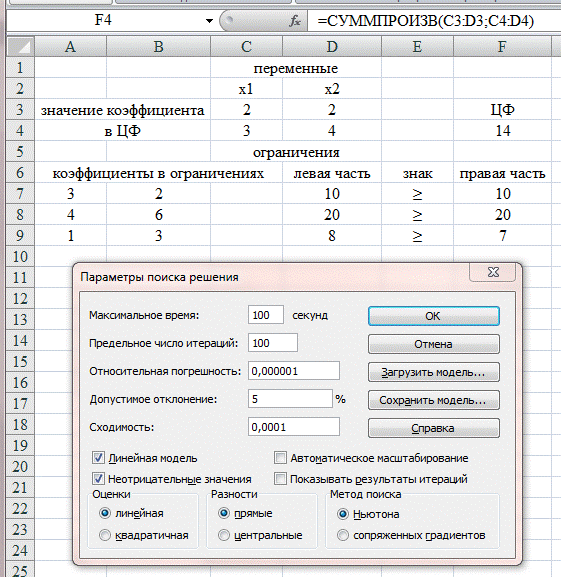
Рис. 2.5. Параметры поиска решения

 

Далее нажимаем «ОК» в окне «Параметры поиска решения».

Затем нажимаем «Выполнить» в окне «Поиск решения».

В окне «Результаты поиска решения» переводим курсор на «Сохранить найденное решение» и «Результаты». Нажимаем «ОК».

Полученное решение означает, что максимум функции равен 14 при х₁ = 2, х₂ = 2 (рис. 2.6).

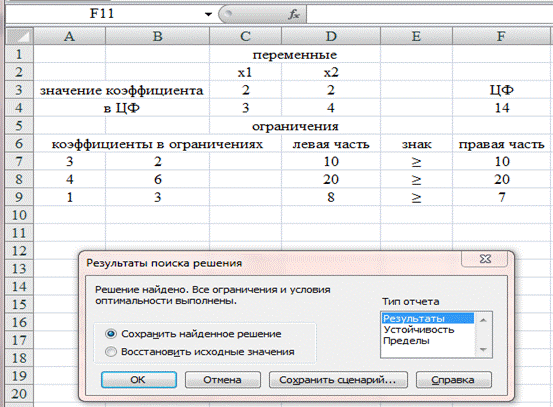
Рис. 2.6. Результаты поиска решения

 

Отчет по результатам решения задачи представлен на рис. 2.7.

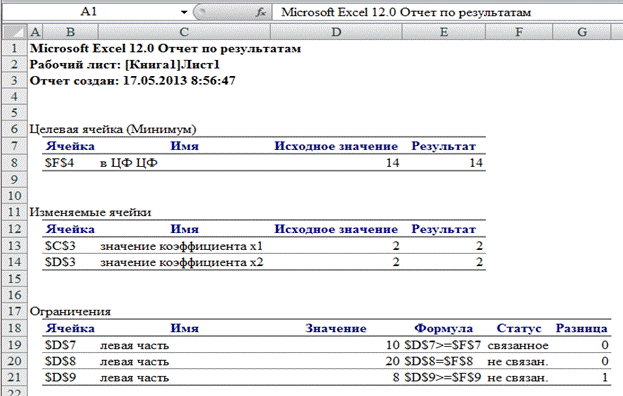
Рис. 2.7. Отчет по результатам решения задачи

Задание 3

 

Рассчитайте параметры моделей экономически выгодных размеров заказываемых партий.

Хозяйственный отдел крупного больничного комплекса использует за год 900 упаковок моющего средства «Comet» весом 400 гр. Стоимость заказа – 200 руб., стоимость хранения одной упаковки в год – 2 руб. 60 коп. Доставка заказа осуществляется в течение трех дней. Хозяйственный отдел работает 300 дней в году.

Определите:

- оптимальный объем заказа;

- годовые расходы на хранение запасов;

- период поставок;

- точку заказа.

 

Оптимальный размер заказываемой партии рассчитывается по формуле Уилсона:

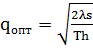, (3.1)

где λ – годовой спрос;

s – накладные расходы;

Т – период (год);

h – стоимость хранения.

Рассчитаем оптимальный объем заказа:

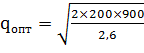= 372 уп.

Рассчитаем годовые расходы на хранение:

2,6 * 372 / 2 = 483,6 руб.

Рассчитаем период поставки:

372 / 900 * 300 = 134 дня.

Рассчитаем точку заказа:

3 * 900 / 300 = 9 уп.

 

Задание 4

 

В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.) в тот момент, когда оба бухгалтера заняты обслуживанием ранее обратившихся коллег, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно λ = 16 , а среднее время, которое затрачивает бухгалтер на оформление документа, – 10 мин. (Т_ср = 1 / μ).

Оцените основные характеристики работы данной бухгалтерии как системы массового обслуживания (СМО) с отказами (указание руководства не допускать непроизводительных потерь рабочего времени!). Определите, сколько бухгалтеров должно работать в бухгалтерии в отведенные дни с сотрудниками, чтобы вероятность обслуживания сотрудников была выше 85%.

 

Решение:

 

Вероятность отказа в обслуживании рассчитывается по формуле:

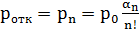, (4.1)

где 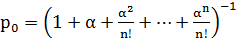; (4.2)

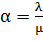. (4.3)

Относительная пропускная способность (В), т.е. вероятность того, что заявка будет обслужена, рассчитывается по формуле:

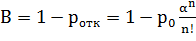. (4.4)

Абсолютную пропускную способность (А) получим, умножив поток сотрудников, обращающихся в бухгалтерию (λ) на (В):

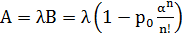. (4.5)

Среднее число занятых каналов рассчитывается по формуле:

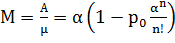. (4.6)

Рассчитаем нагрузку на систему (рис. 4.1).

Рис. 4.1. Расчет нагрузки на систему

 

Рассчитаем вероятность P₀ в ячейке С6 без степени (-1) для числа (1) первого канала (рис. 4.2).

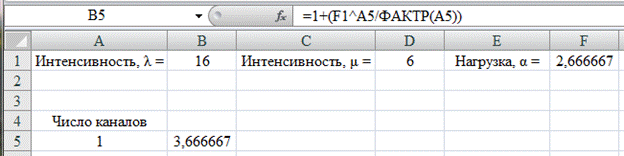
Рис. 4.2. Расчет вероятности

 

Рассчитаем вероятность для остальных каналов меняя в формуле число (1) первого канала на ячейку выше и скопируем для ячеек В6:В14 (рис. 4.3).

Далее рассчитаем вероятность Р₀ в ячейке С5 ставя ячейку В5 в степень (-1) и скопируем формулу в ячейки С6:С14 (рис. 4.4).

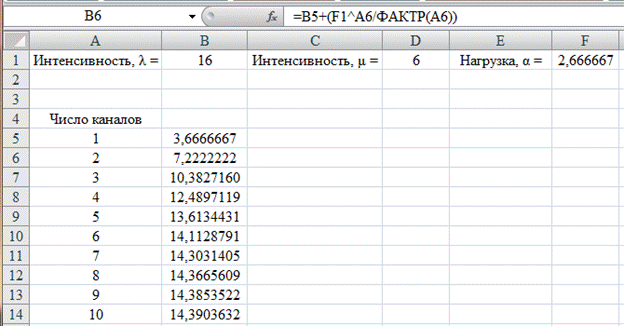
Рис. 4.3. Расчет вероятности

 

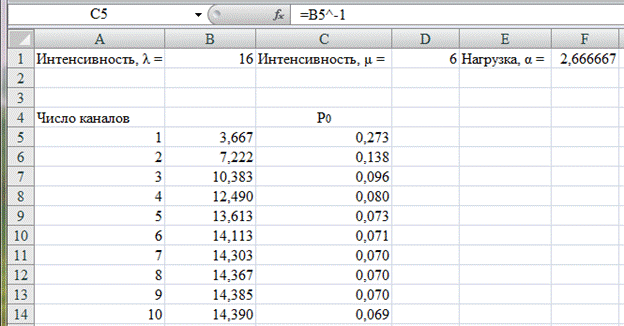
Рис. 4.4. Расчет вероятности Р₀

 

Рассчитаем вероятность отказа в обслуживании (Р_отк) в ячейке D5 и скопируем формулу в ячейки D6:D14 (рис. 4.5).

Расчет относительной пропускной способности (В), т.е. вероятности того, что заявка будет обслужена представлен на рис. 4.6.

 

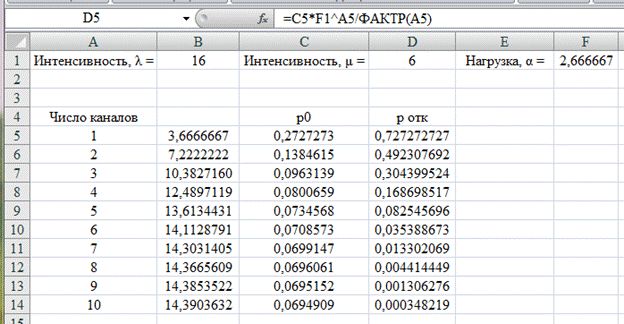
Рис. 4.5. Расчет вероятности отказа в обслуживании

 

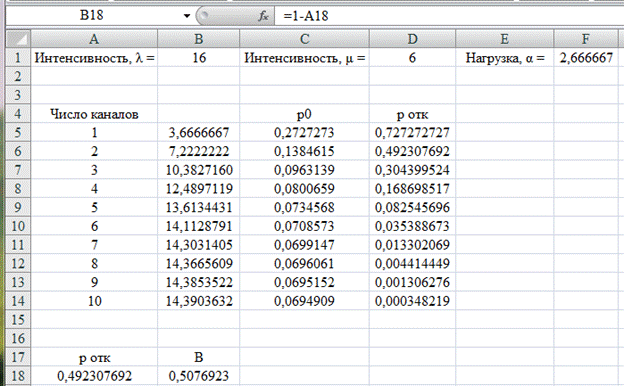
Рис. 4.6. Расчет вероятности обслуживания заявки

 

Расчет абсолютной пропускной способности (А) представлен на рис. 4.7.

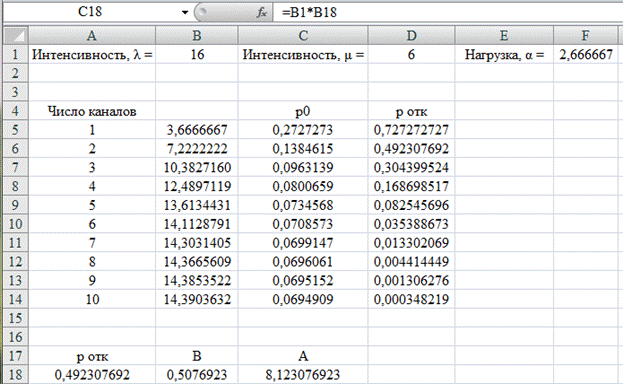
Рис. 4.7. Расчет абсолютной пропускной способности

 

Расчет среднего числа занятых каналов представлен на рис. 4.8.

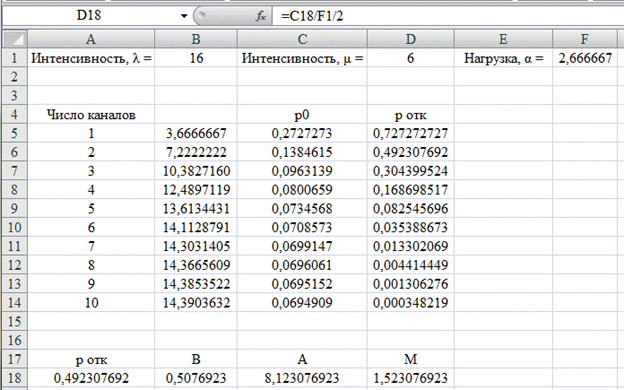
Рис. 4.8. Расчет среднего числа занятых каналов

 

Таким образом, можно сказать, что СМО в значительной мере перегружены: из двух бухгалтеров занято в среднем 1,5, а из обращающихся в бухгалтерию сотрудников около 49,2% остаются необслуженными.

Из графика на рис. 4.9 (Мастер диаграмм Excel / Точечная) видно, что минимальное число каналов обслуживания, при котором вероятность обслуживания бухгалтерией сотрудников будет выше 85%, равно n = 4.

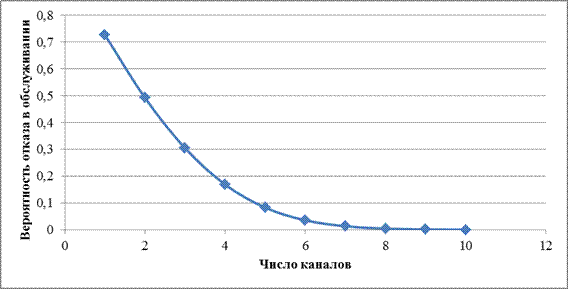
Рис. 4.9. График вероятности отказа в обслуживании

 

 

Задание 5

 

Статистический анализ показал, что случайная величина Х (длительность обслуживания клиента в парикмахерской) следует показательному закону распределения с параметром µ = 0,5), а число клиентов, поступающих в единицу времени (случайная величина Y), – закону Пуассона с параметром λ = 1,8.

Организуйте датчики псевдослучайных чисел для целей статистического моделирования (использования метода Монте-Карло).

Получите средствами MS Excel 15 реализаций случайной величины Х и 15 реализаций случайной величины Y.

 

Решение.

 

Непрерывное равномерное распределение моделирует функция Excel = CЛЧИС() (рис. 5.1).

Рис. 5.1. Случайные числа

 

Пятнадцать реализаций случайных величин длительности интервала между очередными клиентами парикмахерской содержаться в ячейках C4:Q4. Для получения, например, содержимого ячейки С4 использована функция =(-1/1,8*LN(С3) (рис. 5.2).

Рис. 5.2. Расчет времени между клиентами парикмахерской

Соответственно, кумулятивным образом (строка 6 рис. 5.3) на временной оси [0, Т] зафиксировано время T_i (i = 1, 2, …, 15) поступления клиентов (в минутах, с округлением!).

Для получения реализации случайной величины длительности обслуживания клиентов в соответствующую ячейку электронной таблицы (строки 7 и 9 рис. 5.3) записывается формула =60*(1/0,5)*LN(СЛЧИС()).

Расчет времени окончания обслуживания клиентов работниками парикмахерской осуществляется по первому работнику – суммирование строк 6 и 7 рис. 5.3, по второму работнику – суммирование строк 6 и 9 рис. 5.3.

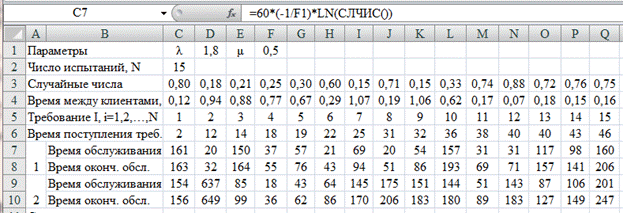
Рис. 5.3. Расчет времени обслуживания по работникам

 

Далее последовательно сравниваются время окончания обслуживания каналами (строки 8 и 10 рис. 5.4) и время поступления клиентов (строка 6 рис. 5.4). Соответственно, в счетчике отказов (строка 11 рис. 5.4) фиксируется 0 (клиент принят к обслуживанию) или 1 (клиенту отказано в обслуживании).

В соответствии со счетчиком отказов зафиксировано 9 отказов. Статистическая оценка вероятности отказа данной СМО при N = 15 составляет 0,6 (9 / 15).

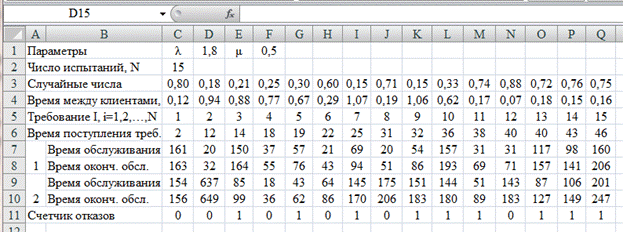
Рис. 5.4. Табличное представление имитации

Список использованных источников

1. Гетманчук А.В., Ермилов М.М. Экономические методы и модели: учеб. пособие. – М.: Дашков и К°, 2013. – 188 с. 2. Гармаш А.Н., Орлова И.В. Математические методы в управлении: учеб.… 3. Математическое программирование: учебник / под ред. К.В. Балдина. – 2-е изд., перераб. и доп. – М.: Дашков и К°,…