рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Информатика
- /
- Решение оптимизационных задач средствами EXCEL
Реферат Курсовая Конспект
Решение оптимизационных задач средствами EXCEL
Решение оптимизационных задач средствами EXCEL - раздел Информатика, ...

КАФЕДРА ЭКОНОМИКО-МАТЕМАТИЧЕСКИХ МЕТОДОВ И МОДЕЛЕЙ
Орлова И. В., Орлов П.В.
Решение оптимизационных задач средствами EXCEL.
Краткий конспект лекций и лабораторная работа № 1 по курсу «Экономико-математические методы и прикладные модели»
Москва
2001 г.
Оглавление
решение систем линейных уравнений методом жордана - гаусса............................... 3
Общая задача оптимизации................................................................................................... 5
Графический метод решения задач линейного программирования................................. 6
Симплексный метод решения задачи линейного программирования........................... 14
Технология решения задач линейного программирования с помощью Поиска решений в среде EXCEL...................................................................................................................................... 17
Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений.................................................................................................................................... 32
Задания к контрольной работе.......................................................................................... 40
ЗАДАЧА 1................................................................................................................................. 40
ЗАДАЧА 2................................................................................................................................. 40
Список литературы, имеющейся в библиотеке ВЗФЭИ................................................ 44
решение систем линейных уравнений
методом жордана - гаусса
Пример 1.Решить методом Жордана-Гаусса систему линейных уравнений:
а) Х1 + Х2 + 2Х3 = -1
2Х1 - Х2 + 2Х3 = -4
4Х1 + Х2 + 4Х3 = -2
Решение:
Составим расширенную матрицу
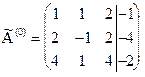
1 Итерация.
В качестве направляющего элемента выбираем элемент  . Преобразуем первый столбец в единичный. Для этого к второй и третьей строкам прибавляем первую строку, соответственно умноженную на -2 и -4. Получим матрицу:
. Преобразуем первый столбец в единичный. Для этого к второй и третьей строкам прибавляем первую строку, соответственно умноженную на -2 и -4. Получим матрицу:
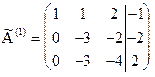
На этом первая итерация закончена.
2 Итерация.
Выбираем направляющий элемент 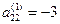 . Так как
. Так как  , то делим вторую строку на -3. Затем умножаем вторую строку на 1 и 3 и складываем соответственно с первой и третьей строками. Получим матрицу:
, то делим вторую строку на -3. Затем умножаем вторую строку на 1 и 3 и складываем соответственно с первой и третьей строками. Получим матрицу:

3 Итерация.
Выбираем направляющий элемент  . Так как
. Так как 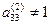 , то делим третью строку на -2. Преобразуем третий столбец в единичный. Для этого умножаем третью строку на -4/3 и -2/3 и складываем соответственно с первой и второй строками. Получим матрицу:
, то делим третью строку на -2. Преобразуем третий столбец в единичный. Для этого умножаем третью строку на -4/3 и -2/3 и складываем соответственно с первой и второй строками. Получим матрицу:

откуда Х1 = 1, Х2 = 2, Х3 = -2.
Пример 2.Решить методом Жордана - Гаусса систему линейных уравнений:
Х1 + 2Х2 + 2Х3 +22Х4 –4Х5= 11
Х1 +2Х2 + Х3 +16Х4–4Х5= 9
Х1 + Х2 + Х3 +12Х4 -2Х5= 6
Решение:
Составим расширенную матрицу
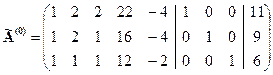
1 Итерация.
В качестве направляющего элемента выбираем элемент  . Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на -1. Получим матрицу:
. Преобразуем первый столбец в единичный. Для этого ко второй и третьей строкам прибавляем первую строку, соответственно умноженную на -1. Получим матрицу:
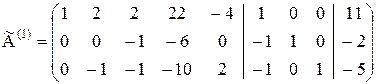
На этом первая итерация закончена.
2 Итерация.
Выбираем направляющий элемент  . Умножаем третью строку на -1. Преобразуем второй столбец в единичный. Для этого к первой строке прибавляем третью строку, соответственно умноженную на -2.
. Умножаем третью строку на -1. Преобразуем второй столбец в единичный. Для этого к первой строке прибавляем третью строку, соответственно умноженную на -2.
Получим матрицу:

3 Итерация.
Выбираем направляющий элемент  . Так как
. Так как  , то умножаем вторую строку на –1. Преобразуем третий столбец в единичный. Для этого вторую строку складываем с третьей строкой. Получим матрицу:
, то умножаем вторую строку на –1. Преобразуем третий столбец в единичный. Для этого вторую строку складываем с третьей строкой. Получим матрицу:

| Х1 | Х2 | Х3 | Х4 | Х5 | |||||
| -4 | |||||||||
| -4 | |||||||||
| -2 | |||||||||
| -4 | |||||||||
| -1 | -6 | -1 | -2 | ||||||
| -1 | -1 | -10 | -1 | -5 | |||||
| -1 | |||||||||
| -1 | -6 | -1 | -2 | ||||||
| -2 | -1 | ||||||||
| -1 | |||||||||
| -1 | |||||||||
| -2 | -1 | ||||||||
| -1 | |||||||||
| -2 | -1 | ||||||||
| -1 |
Исходная система эквивалентна следующей системе уравнений:
Х1 + 2Х4 = 1
Х2 +4Х4 -2Х5= 3
Х3 +6Х4= 2
Система уравнений имеет бесконечное множество решений.
Общее решение имеет вид:
Х1 = 1-2Х4
Х2 = 3-4Х4 +2Х5
Х3 = 2-6Х4.
переменные Х1, Х2, Х3 являются основными (или базисными). Любое частное решение получается из общего путем придания конкретных значений свободным переменным. Если свободные переменные Х4 и Х5 положить равными нулю, то получим первое базисное решение Х1 = 1, Х2 = 3, Х3 = 2, Х4 = 0, Х5=0.
Первое базисное решение имеет вид: (1,3,2,0,0).
Общее число групп основных переменных, т.е. базисных решений не более, чем  =
=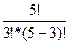 =
=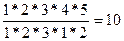 .
.
Если все компоненты базисного решения неотрицательны, то такое решение называется опорным.
Общая задача оптимизации
Целью работы коммерческой фирмы является получение прибыли. Любое управленческое решение (будь то решение о количестве приобретаемого товара, или решение о назначении цены на реализуемый товар, или решение о подаче рекламы в газету и т.д.) будет влиять на прибыль в большую или меньшую сторону. Эти решения являются оптимизационными, то есть всегда существует возможность выбрать лучшее решение из нескольких возможных. Представим себе, что все управленческие решения принимаются наилучшим образом. То есть, все параметры, на которые может влиять фирма, являются оптимальными. Тогда фирма будет получать максимальную прибыль (больше получить при данных условиях невозможно). Для того чтобы определить, насколько управленческие решения, принимаемые работниками фирмы оптимальны, можно использовать методы математического программирования.
В экономике оптимизационные задачи возникают в связи с многочисленностью возможных вариантов функционирования конкретного экономического объекта, когда возникает ситуация выбора варианта, наилучшего по некоторому правилу, критерию, характеризуемому соответствующей целевой функцией (например, иметь минимум затрат, максимум продукции).
Оптимизационные модели отражают в математической форме смысл экономической задачи, и отличительной особенностью этих моделей является наличие условия нахождения оптимального решения (критерия оптимальности), которое записывается в виде функционала. Эти модели при определенных исходных данных задачи позволяют получить множество решений, удовлетворяющих условиям задачи, и обеспечивают выбор оптимального решения, отвечающего критерию оптимальности.
В общем виде математическая постановка задачи математического программирования состоит в определении наибольшего или наименьшего значения целевой функции f (х1, х2, ..., хn) при условиях gi(х1, х2, ..., хn) £ bi; (i =1,2,…m), где f и gi; – заданные функции, а bi – некоторые действительные числа.
задачи математического программирования делятся на задачи линейного и нелинейного программирования. если все функции f и gi линейные, то соответствующая задача является задачей линейного программирования. Если же хотя бы одна из указанных функций нелинейная, то соответствующая задача является задачей нелинейного программирования.
В общем виде задача линейного программирования (ЗЛП) ставится следующим образом:
Найти вектор 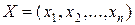 , максимизирующий линейную форму
, максимизирующий линейную форму
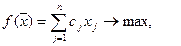 (1)
(1)
и удовлетворяющий условиям
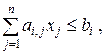 (2)
(2)
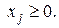
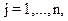 (3)
(3)
Линейная функция 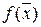 называется целевой функцией задачи. Условия (2) называются функциональными, а (3) - прямыми ограничениями задачи.
называется целевой функцией задачи. Условия (2) называются функциональными, а (3) - прямыми ограничениями задачи.
Вектор 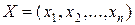 , компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.
, компоненты которого удовлетворяют функциональным и прямым ограничениям задачи, будем называть планом, или допустимым решением ЗЛП.
Все допустимые решения образуют область определения задачи линейного программирования, или область допустимых решений. Допустимое решение, максимизирующее целевую функцию f(x), называется оптимальным планом задачи

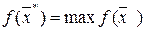 ,
,
где 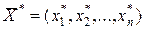 - оптимальное решение ЗЛП. Будем считать, что ЗЛП записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательны.
- оптимальное решение ЗЛП. Будем считать, что ЗЛП записана в канонической форме, если ее целевая функция максимизируется, ограничения имеют вид равенств с неотрицательной правой частью и все переменные неотрицательны.
На практике хорошо зарекомендовали себя следующие модели, относящиеся к оптимизационным: модели определения оптимальной производственной программы, модели оптимального смешивания компонентов, оптимального раскроя, оптимального размещения предприятий некоторой отрасли на определенной территории, модели формирования оптимального портфеля ценных бумаг, модели транспортной задачи.
Графический метод решения задач линейного программирования.
Наиболее простым и наглядным методом линейного программирования (ЛП) является графический метод. Он применяется для решения задач ЛП с двумя переменными.
Рассмотрим задачу ЛП в стандартной форме записи:

Положим n=2, т.е. рассмотрим эту задачу на плоскости. Пусть система неравенств совместна (имеет хотя бы одно решение).
Каждое неравенство этой системы геометрически определяет полуплоскость с граничной прямой ai1 x1 + ai2 x2 = bi , i=1,2,…m. Условия неотрицательности определяют полуплоскости, соответственно, с граничными прямыми x1=0,x2 =0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, многоугольником, неограниченной многоугольной областью.
Таким образом, геометрически задача линейного программирования (ЗЛП) представляет собой отыскание такой точки многоугольника решений, координаты которой доставляют линейной функции цели максимальное (минимальное) значение, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости. Определим, какую часть плоскости описывает неравенство 2х1+3х2£ 12. Во-первых, построим прямую 2х1+3х2=12. Эта прямая проходит через точки (6, 0) и (0, 4). Для того чтобы определить, какая полуплоскость удовлетворяет неравенству необходимо выбрать любую точку на графике, не принадлежащую прямой, и подставить ее координаты в неравенство. Если неравенство будет выполняться, то данная точка является допустимым решением и полуплоскость, содержащая точку, удовлетворяет
неравенству. Удобной для использования при подстановке в неравенство является начало координат. Подставим х1=х2=0 в неравенство 2х1+3х2£12. Получим 2´0+3´0£12. Данное утверждение является верным, следовательно, неравенству 2х1+3х2£12 соответствует нижняя полуплоскость, содержащая точку (0.0). Это отражено на графике, изображенном на рис.1.
 |
Рис. 1. Неравенству 2х1+3х2£12 соответствует нижняя полуплоскость.
Аналогично можно изобразить графически каждое ограничение задачи линейного программирования.
Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее. Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью допустимых решений или областью определения. Необходимо помнить, что область допустимых решений удовлетворяет
.
условиям неотрицательности (xj ³0, j=1,…,n). Координаты любой точки, принадлежащей области определения являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении задач ЛП используют вектор–градиент, координаты которого являются частными производными целевой функции, т.е.
 .
.
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая 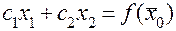 , перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.
, перпендикулярная вектору–градиенту, является линией уровня целевой функции. В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине “a”. Меняя значение “a”, получим семейство параллельных прямых, каждая из которых является линией уровня.
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – убывает.
С геометрической точки зрения в задаче линейного программирования ищется такая угловая точка или набор точек из допустимого множества решений, на котором достигается самая верхняя (нижняя) линия уровня, расположенная дальше (ближе) остальных в направлении наискорейшего роста.
Графический метод решения ЗЛП состоит из следующих этапов.
1. Строится многоугольная область допустимых решений ЗЛП – ОДР,
2. Строится вектор-градиент ЦФ в какой-нибудь точке Х0 принадлежащей ОДР –
 .
.
3. Линия уровня C1x1+C2x2 = а (а–постоянная величина) - прямая, перпендикулярная вектору –градиенту 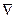 – передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
– передвигается в направлении этого вектора в случае максимизации f(x1,x2) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x1,x2).
4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x1,x2), найденное в получаемой точке, является максимальным.
При минимизации f(x1,x2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x1,x2) не существует.
Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
Рассмотрим графическое решение задач линейного программирования на следующем примере.
Задача 1. о планировании выпуска продукции пошивочному предприятию. (Задача о костюмах).
Намечается выпуск двух видов костюмов - мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм - 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат. Tребуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского - 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.
Модель задачи.
Введем следующие обозначения: х1 - число женских костюмов; x2 - число мужских костюмов.
Прибыль от реализации женских костюмов составляет 10х1, а от реализации мужских 20х2, т.е. необходимо максимизировать целевую функцию
f(x) = 10´ х1 + 20´ х2 -> max.
Ограничения задачи имеют вид:
х1 + х2 £ 150
2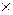 х1 + 0.5
х1 + 0.5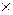 х2 £ 240
х2 £ 240
х1 + 3.5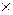 х2 £ 350
х2 £ 350
х2³ 60
х1 ³ 0
Первое ограничение по труду х1 + х2 £ 150. Прямая х1 + х2 = 150 проходит через точки (150, 0) и (0, 150).

Рис. 2. Решением первого неравенства является нижняя полуплоскость.
Второе ограничение по лавсану 2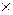 х1 + 0.5
х1 + 0.5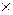 х2 £ 240. Прямая 2
х2 £ 240. Прямая 2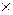 х1 + 0.5
х1 + 0.5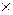 х2 = 240 проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х1 + 3.5
х2 = 240 проходит через точки (120, 0) и (0, 480). Третье ограничение по шерсти х1 + 3.5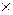 х2 £ 350. Добавим четвертое ограничение по количеству мужских костюмов х2 ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60. На рис.3. заштрихована область допустимых решений.
х2 £ 350. Добавим четвертое ограничение по количеству мужских костюмов х2 ³ 60. Решением этого неравенства является полуплоскость, лежащая выше прямой х2 = 60. На рис.3. заштрихована область допустимых решений.
Рис. 3. Заштрихована область допустимых решений.

Для определения направления движения к оптимуму построим вектор-градиент Ñ, координаты которого являются частными производными целевой функции, т.е. 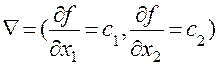 = (10;20).
= (10;20).
Что бы построить этот вектор, нужно соединить точку (10;20) с началом координат. При максимизации целевой функции необходимо двигаться в направлении вектора-градиента, а при минимизации — в противоположном направлении. Для удобства можно строить вектор, пропорциональный вектору Ñ. Так, на рис. 2.1.6. изображен вектор градиент (30;60).
В нашем случае движение линии уровня будем осуществлять до ее выхода из области допустимых решений. в крайней, угловой точке достигается максимум целевой функции. Для нахождения координат этой точки достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума: х1 + 3.5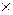 х2 = 350
х2 = 350
х1 + х2 = 150 .
Отсюда легко записать решение исходной ЗЛП: max f(x) = 2300 и достигается при x1=70 и x2=80 (рис. 4.)


Рис.4. Максимум целевой функции достигается в точке (70, 80).
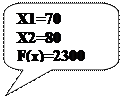 |
Задача 2.Для изготовления двух видов продукции А1 и А2 используют три вида ресурсов S1, S2, S3, запасы которых составляют 18, 16 и 5 усл.ед. Расход ресурсов на 1 ед. продукции приведен в таблице:
| Виды ресурсов | Запасы ресурсов | Расходы ресурсов на 1 изд. | |
| А1 | А2 | ||
| S1 | 18 | 1 | 3 |
| S2 | 16 | 2 | 1 |
| S3 | 5 | - | 1 |
| Прибыль | 2 руб. | 3 руб. |
Необходимо составить такой план производства продукции, который обеспечит наибольшую прибыль от ее реализации.
Составим экономико-математическую модель (ЭММ) задачи.
Пусть надо выпустить изделий A1 - x1 шт., а изделий А2 - x2 шт. Тогда прибыль F = 2x1 + 3x2 Þ max
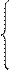 x1 + 3x2 £ x1 + 3x2 £
| 18 |
| 2x1 + x2 £ | 16 |
| x2 £ | 5 |
| x1 ³ 0, | x2 ³ 0 |
Решим задачу графически.
max F достигается в т. С т.С x1 + 3 x2 = 18 Þ - …Симплекс-метод с естественным базисом
Для определенности предположим, что первые m векторов матрицы системы уравнений составляют единичную матрицу. Тогда первоначальный опорный план… Проверка на оптимальность опорного плана проходит с помощью признака… Математический признак оптимальности состоит из следующих двух теорем:Сформулируем экономико-математическую модель задачи.
Прибыль от реализации женских костюмов составляет 10х1, а от реализации мужских 20х2, т.е. необходимо максимизировать целевую функцию f(x) = 10´ х1 + 20´ х2 -> max. Ограничения задачи имеют вид:Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
Обозначьте через Х1, Х2 количество костюмов каждого типа.В нашей задаче оптимальные значения вектора Х =(Х1, Х2,) будут помещены в ячейкахA2:B2, оптимальное значение целевой функции в ячейке C3.
Ввести исходные данные.
Введите исходные данные задачи, как показано на рис.1.

Рис. 1.
Ввести зависимость для целевой функции
•Курсор на кнопку «Мастер функций»,расположенную на панели инструментов. •М1.На экране появляется диалоговое окно «Мастер функций шаг 1 из 2» • Курсор в окно«Категория» накатегорию «Математические».Ввести ограничения
•Указатель мышки на кнопку «Добавить.Появляется диалоговое окно «Добавление ограничения» •В строке «Ссылка на ячейку» введите адрес $С$4. •Ввести знак ограничения ≤.Ввести параметры для решения ЗЛП
Рис.11Решение
Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
Обозначьте через Х1, Х2, Хз, Х4 количество ковров каждого типа.В нашей задаче оптимальные значения вектора Х =(Х1, Х2, Хз, Х4) будут помещены в ячейкахВЗ:ЕЗ, оптимальное значение целевой функции в ячейке F4.
Ввести исходные данные.
)Введем исходные данные в созданную форму. В результате получим (Рисунок 14):
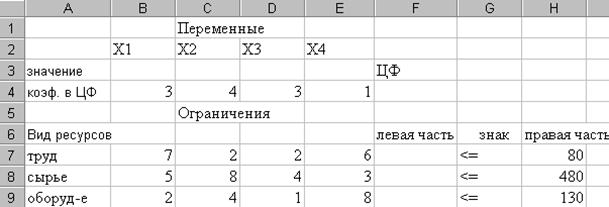 Рисунок 14. Данные введены.
Рисунок 14. Данные введены.
Введем зависимость для целевой функции
• Курсор на кнопку Мастер функций. На экране диалоговое окно Мастер функций шаг 1 из 2. • Курсор в окно Категория на категорию Математические.Ввод ограничений.
Задача 5.
в планируемом периоде необходимо обеспечить производство 300 тыс. однородных новых изделий, которые могут выпускаться на четырех филиалах… Необходимо найти такой вариант распределения объемов производства продукции и… Таблица Показатель Филиал предприятия …Решение
Xi - объем выпускаемой продукции на i-м филиале предприятия. = 83X1+89X2+95X3+98X4 -> min, ОграниченияВариант 1
Max f ( x ) = 3X1 + 2X2
X1 + 2X2 ≤ 11
2X1 - X2 ≥ 5
X1 + 3X2 ≥ 14
X1 , X2 ≥ 0
Вариант 2
Max f ( x ) = 3X1 + 2X2
X1 + 2X2 ≤ 12
2X1 - X2 ≥ 7
X1 + 3X2 ≥ 14
X1 , X2 ≥ 0
Вариант 3
Max f ( x ) = 3X1 + 2X2
X1 + 2X2 ≥ 10
2X1 - X2 ≤ 18
X1 + 3X2 ≤ 13
X1 , X2 ≥ 0
Вариант 4
Min f ( x ) = 3X1 + 2X2
X1 + 2X2 ≥10
2X1 - X2 ≥ 10
X1 + 3X2 ≤ 13
X1 , X2 ≥ 0
Вариант 5
Max f ( x ) = 4х1+ 3х2
х1 + 2х2 £ 10
х1 + 2х2 ³ 2
2х1 + х2 £ 10
х1 ³ 0, х2 ³ 0
Вариант 6
Min f ( x ) = 3X1 + 2X2
X1 + 2X2 ≥12
2X1 - X2 ≥ 12
X1 + 3X2 ≤ 14
X1 , X2 ≥ 0
Вариант 7
Max f ( x ) = 3х1+ 5х2
х1 + х2 £ 5
3х1 + 2 х2 £ 8
х1 ³ 0, х2 ³ 0
Вариант 8
Min f ( x ) = 3X1 + 2X2
X1 + 2X2 ≤ 11
2X1 - X2 ≥ 5
X1 + 3X2 ≥ 14
X1 , X2≥ 0
Вариант 9
Max f ( x ) = 3х1+ х2
2х1 + 3х2 ³ 12
-х1 + х2 £ 2
2х1 - х2 £ 2
х1 ³ 0, х2 ³ 0
Вариант 10
Max f ( x ) = 3х1+ х2
х1 + х2 £ 5
0.5х1 + х2 ³ 3
х1 - х2 ³ 1
ЗАДАЧА 2.
Используя Поиск решения, решить задачу оптимального использования ресурсов на максимум общей стоимости. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.
В каждой задаче требуется:
1. Определить план выпуска продукции из условия максимизации его стоимости.
2. Определите ценность каждого ресурса (двойственные оценки) и его приоритет при решении задачи увеличения запаса ресурсов.
3. Определите суммарную стоимостную оценку ресурсов, используемых при производстве единицы каждого изделия. Выпуск какой продукции нерентабелен?
4. На сколько уменьшится стоимость выпускаемой продукции при принудительном выпуске единицы нерентабельной продукции?
Кроме того, в каждом варианте необходимо выполнить еще два пункта задания.
Вариант 1
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Тип | Нормы расхода сырья на одно изделие | Запасы | |||
| сырья | А | Б | В | Г | сырья |
| I | |||||
| II | |||||
| III | |||||
| Цена изделия |
5. Определить, как изменятся общая стоимость продукции и план ее выпуска при увеличении запасов сырья I и II вида на 4 и 3 единицы соответственно и уменьшении на 3 единицы сырья III вида.
6. Определить целесообразность включения в план изделия «Д» ценой 10 ед., на изготовление, которого расходуется по две единицы каждого вида сырья ед.
Вариант 2
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Тип | Нормы расхода сырья на одно изделие | Запасы | ||||
| сырья | А | Б | В | Г | сырья | |
| I | ||||||
| II | ||||||
| III | ||||||
| Цена изделия |
5. Определить, как изменятся общая стоимость продукции и план выпуска при увеличении запасов сырья II и III вида на 120 и 160 ед. соответственно и одновременном уменьшении на 60 ед. запасов сырья I вида;
6. Определить целесообразность включения в план изделия «Д» ценой 12 ед., на изготовление которого расходуется по две единицы каждого вида сырья.
Вариант 3
Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Тип | Нормы расхода сырья на одно изделие | Запасы | ||
| Сырья | А | Б | В | сырья |
| I | ||||
| II | ||||
| III | ||||
| Цена |
5. Определить, как изменится общая прибыль продукции и план выпуска при увеличении запасов сырья I и III вида на 4 ед. каждого;
6.Определить целесообразность включения в план изделия «Г», на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого вида сырья ценой 13 ед. и изделия «Д» на изготовление которого расходуется по две единицы каждого вида сырья ценой 12 ед.
Вариант 4
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Тип | Нормы расхода сырья на одно изделие | Запасы | ||||
| Сырья | А | Б | В | Г | сырья | |
| I | ||||||
| II | ||||||
| III | ||||||
| Цена изделия |
5. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья I и II вида на 8 и 10 ед. соответственно и одновременном уменьшении на 5 ед. запасов сырья III вида;
6. Определить целесообразность включения в план изделия «Д» на изготовление которого расходуется по две единицы каждого вида сырья и ожидается прибыль 10 ед.
Вариант 5
На основании информации приведенной в таблице была решена задача оптимального использования ресурсов на максимум общей стоимости.
| Ресурсы | Нормы затрат ресурсов на единицу продукции | Запасы | ||
| I вид | II вид | III вид | ||
| Труд | ||||
| Сырье | ||||
| Оборудование | ||||
| Цена |
5. Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья на 18 единиц;.
6. Определить целесообразность включения в план изделия четвертого вида на изготовление которого расходуется по две единицы каждого вида ресурсов ценой 70 ед.
Вариант 6
На предприятии выпускается три вида изделий, используется при этом три вида сырья:
| Сырье | Нормы затрат ресурсов на единицу продукции | Запасы | ||||
| А | Б | В | сырья | |||
| I | ||||||
| II | ||||||
| III | ||||||
| Цена | ||||||
5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 45 кг., а II - уменьшить на 9кг.?
6. Целесообразно ли выпускать изделие Г ценой 11 единиц, если нормы затрат сырья 9, 4 и 6 кг.?
Вариант 7
Для изготовления трех видов продукции используют четыре вида ресурсов. Запасы ресурсов, нормы расхода и цена каждого продукта приведены в таблице.
| Ресурсы | Нормы затрат ресурсов на единицу продукции | Запасы | ||
| I вид | II вид | III вид | ||
| Труд | ||||
| Сырье 1 | ||||
| Сырье 2 | ||||
| Оборудование | ||||
| Цена |
5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 24?
6. Целесообразно ли выпускать изделие четвертого вида ценой 11 единиц, если нормы затрат ресурсов 8, 4, 20 и 6 единиц.?
Вариант 8
Предприятие выпускает 4 вида продукции и использует 3 типа основного оборудования: токарное, фрезерное, шлифовальное. Затраты на изготовление единицы продукции приведены в таблице; там же указан общий фонд рабочего времени, а также цена изделия каждого вида.
| Тип | Нормы расхода сырья на одно изделие | Общий фонд | ||||
| оборудования | А | Б | В | Г | раб. времени | |
| Токарное | ||||||
| Фрезерное | ||||||
| Шлифовальное | ||||||
| Цена изделия |
5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если фонд времени шлифовального оборудования увеличить на 24 часа ?
6. Целесообразно ли выпускать изделие «Д» ценой 11 единиц, если нормы затрат оборудования 8, 2 и 2 ед.?
Вариант 9
На предприятии выпускается три вида изделий, используется при этом три вида сырья:
| Сырье | Нормы затрат ресурсов на единицу продукции | Запасы | |||
| А | Б | В | сырья | ||
| I | 430 кг | ||||
| II | 460 кг | ||||
| III | 420 кг | ||||
| Цена |
5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 80 кг., а II - уменьшить на 10кг.?
6. Целесообразно ли выпускать изделие Г ценой 7 единиц, если нормы затрат сырья 2, 4 и 3 кг.?
Вариант 10
Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта приведены в таблице.
| Тип | Нормы расхода сырья на одно изделие | Запасы | ||||
| Сырья | А | Б | В | Г | сырья | |
| I | 0,5 | |||||
| II | ||||||
| III | ||||||
| Цена изделия | 7,5 |
5. Как изменится общая стоимость выпускаемой продукции и план ее выпуска, если запас сырья I вида увеличить на 100 кг, а II - уменьшить на 150кг.?
6. Целесообразно ли выпускать изделие «Д» ценой 10 единиц, если нормы затрат сырья 2, 4 и 3 кг?
Список литературы, имеющейся в библиотеке ВЗФЭИ.
1. Федосеев В.В., Гармаш А.Н., Дайитбегов Д.М., Орлова И.В., Половников В.А. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В.Федосеева. – М.: ЮНИТИ, 1999. – 391 с.
2. Орлова И.В. Экономико-математические методы и модели. Выполнение расчетов в среде ЕХСЕL/ Практикум: Учебное пособие для вузов. - М.:ЗАО Финстатинформ, 2000.-136 с.
[1] Примечание:Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.
[2] Относительные и абсолютные ссылки. В зависимости от выполняемых задач в Excel можно использовать относительные ссылки, определяющие положение ячейки относительно положения ячейки формулы, или абсолютные ссылки, которые всегда указывают на конкретные ячейки. Если перед буквой или номером стоит знак доллара, например, $A$2, то ссылка на столбец или строку является абсолютной. Относительные ссылки автоматически корректируются при их копировании, а абсолютные ссылки — нет.
[3] Адреса ячеек во все диалоговые окна удобно вводить не с клавиатуры, а протаскивая мыщь по ячейкам, чьи адреса следует ввести.
– Конец работы –
Используемые теги: Решение, оптимизационных, задач, средствами, Excel0.089
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение оптимизационных задач средствами EXCEL
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов