Математический анализ
Математический анализ
Семестр
Содержание
Числовые ряды. Критерий Коши сходимости. Свойства сходящихся рядов.
Ряды с неотрицательными членами. Теоремы сравнения. Признаки Даламбера, Коши, Гаусса.
3. Интегральный признак сходимости. Сходимость ряда 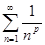 .
.
Абсолютная сходимость. Свойства абсолютно сходящихся рядов.
Условная сходимость. Теорема Лейбница.
Равномерная сходимость функциональной последовательности, ряда. Признак Вейерштрасса.
Непрерывность суммы равномерно сходящегося ряда из непрерывных функций. Почленное интегрирование и дифференцирование ряда.
Степенные ряды. Радиус сходимости. Непрерывность суммы. Почленное интегрирование и дифференцирование.
Разложение элементарных функций в степенные ряды.
Ортонормированные системы функций. Обобщенные ряды Фурье. Тригонометрические ряды Фурье. Теорема сходимости.
11. Дифференциальные уравнения 1-го порядка. Уравнение  . Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида
. Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида  .
.
Линейное дифференциальное уравнение 1-го порядка.
13. Дифференциальное уравнение n-ного порядка. Задача Коши для уравнения 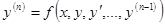 . Понижение порядка дифференциального уравнения.
. Понижение порядка дифференциального уравнения.
14. Линейное дифференциальное уравнение n-ного порядка. Свойства линейного однородного дифференциального уравнения.
Линейная зависимость функций. Определитель Вронского.
Фундаментальная система решений линейного однородного уравнения.
Линейное неоднородное уравнение. Принцип суперпозиции.
Метод вариации постоянных.
Линейное однородное дифференциальное уравнение с постоянными коэффициентами. Характеристическое уравнение. Общее решение.
Метод неопределенных коэффициентов для нахождения частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами.
Определение. Если существует , то говорят, что сходится бесконечный ряд (другое обозначение ) (2) и его сумма равна .
Если же не существует, либо бесконечен, то говорят, что ряд (2) расходится.… Пример. (геометрическая прогрессия). Из элементарной алгебры: . Если , то при и , т.е. ряд сходится. Если , то при и…
. Ряд сходится Þ существует . Но частичная сумма ряда имеет вид . Величина не зависит от . Кроме того, при . Поэтому существует . Утверждение… Итак, исследование сходимости ряда и исследование сходимости любого его… Теорема. (1).
Теорема. (Критерий сходимости рядов с неотрицательными членами). Ряд сходится .
. Пусть . Поскольку , последовательность возрастает и, по условию, ограничена. Следовательно, по теореме Вейерштрасса (см. 1-ый семестр), она имеет… Простые следствия из этого критерия – очень полезные теоремы сравнения.
Теорема 1. Пусть для всех и пусть ряд - сходится. Тогда сходится ряд .
Легко доказать, что из сходимости ряда вытекает сходимость ряда . По критерию Коши, примененному к , получаем: . Из полученного неравенства следует,… Обозначим , т.е. , . Очевидны равенства: . Рассмотрим ряды и . Если они…
Теорема. (Лейбниц). Пусть для ряда выполнены условия:
1. ;
2. .
Без доказательства.
Теорема. (Признак Дирихле). Если частичные суммы ряда 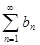 , т.е. суммы
, т.е. суммы 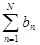 ограниченны в совокупности (т.е.
ограниченны в совокупности (т.е.  ), а последовательность
), а последовательность 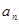 монотонно стремится к 0, то ряд
монотонно стремится к 0, то ряд 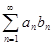 сходится.
сходится.
Без доказательства.
Определение. поточечно сходится к на , если , т.е. .
Пример. Пусть , . Тогда при имеем: . При и . Таким образом, последовательность… Если рассматривать функциональный ряд , составленный из определенных на множестве функций, то под его поточечной…
Следствие. (Необходимый признак сходимости ряда). Положим в критерий Коши . Тогда получаем: , т.е. .
Теорема. (Признак Вейерштрасса). Пусть выполняется неравенство . Пусть, кроме… Доказательство. Достаточно проверить справедливость критерия Коши, т.е. доказать, что . Но последнее неравенство…
Доказательство. Требуется доказать, что функция непрерывна в точке , т.е. . Зафиксируем произвольное . Ввиду равномерной сходимости . В частности, .… Следствие. Сумма равномерно сходящегося ряда, члены которого являются… Доказательство. Применим предыдущую теорему к последовательности частичных сумм ряда.
Теорема 1. Если степенной ряд сходится в точке , то он сходится абсолютно для любого значения такого, что .
Доказательство. Поскольку - сходится, . Следовательно, . (Действительно, взяв… Эта теорема позволяет выяснить структуру множества, на котором сходится степенной ряд.
Доказательство. Так как , ряд сходится. Так как , можно применить теорему Вейерштрасса, из которой и следует утверждение леммы.
Замечание. Лемма отнюдь не утверждает равномерной сходимости степенного ряда… Пусть теперь , т.е. . Выберем так, чтобы . Тогда, по доказанной лемме, ряд сходится на абсолютно и равномерно.…
Лемма. Если для любого отрезка при любом , то .
Доказательство. Для произвольного выберем так, чтобы . Применим к формулу… Для получения разложения заметим, что , и для любого отрезка . Поэтому лемма применима с , и мы получаем: .
Термин “ортогональность” требует некоторых пояснений. Функции на отрезке образуют (бесконечномерное) векторное пространство (сумма функций и… 1. ;
2. ;
Решим сначала вспомогательное уравнение . Это – уже знакомое уравнение с разделяющимися переменными, имеющее решение . Для нахождения решения… В общем случае уравнения , где - непрерывные на функции мы поступаем вполне… Уравнения, не разрешенные относительно производной. Общее уравнение первого порядка можно пытаться решать разными…
Это уравнение называется линейным, поскольку все величины входят в него в первой степени, т.е. линейным образом. Если , то это уравнение называется… Если же , то (1) – линейное неоднородное уравнение.
Удобно записывать уравнения (1) и (2) в операторной форме: и , соответственно, где величину можно рассматривать как…
Определение. Пусть - функции, имеющие все производные до порядка включительно. Определителем Вронского функций называется величина (3).
Определение. Пусть определены ны интервале . Мы назовем их линейно зависимыми,… Функции, которые не являются линейно зависимыми, называются линейно независимыми. Линейная независимость означает, что…
Из предыдущих теорем сразу следует еще одна важная теорема.
Теорема 7. Решения уравнения (2) образуют фундаментальную систему решений… Доказательство. Равносильная переформулировка утверждения теоремы – решения линейно зависимы тогда и только тогда,…
Доказательство. Пусть . Тогда, по лемме 1 (Билет 14), . Таким образом, есть некоторое решение однородного уравнения (2).
Обратно, если и , то и, следовательно, удовлетворяет уравнению (1).
Теорема 3 доказана.
Для того, чтобы отыскать следует воспользоваться системой (14), рассматривая ее как систему линейных уравнений относительно неизвестных с…
Для этого будем искать решения уравнения в виде . При этом (3). Подставим полученные величины в уравнение (1): , или . Поскольку при всех , из… Таким образом, функция удовлетворяет уравнению (1) тогда и только тогда, когда… Далее мы установим вид фундаментальной системы решений уравнения (1) в зависимости от свойств корней уравнения (4).
…
В случае уравнения с постоянными коэффициентами мы указали способы нахождения его фундаментальной системы решений. Используя метод вариации… Пусть (3), где - многочлены, - действительные числа. Согласно принципу… Решения уравнения (4) имеют различный вид в зависимости от того, является или нет число корнем характеристического…
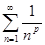 .
. . Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида
. Теорема существования и единственности решения задачи Коши. Уравнения с разделяющимися переменными, однородные уравнения. Уравнения вида  .
.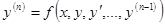 . Понижение порядка дифференциального уравнения.
. Понижение порядка дифференциального уравнения.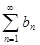 , т.е. суммы
, т.е. суммы 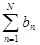 ограниченны в совокупности (т.е.
ограниченны в совокупности (т.е.  ), а последовательность
), а последовательность 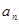 монотонно стремится к 0, то ряд
монотонно стремится к 0, то ряд 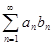 сходится.
сходится.