рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Линейное дифференциальное уравнение 1-го порядка.
Реферат Курсовая Конспект
Линейное дифференциальное уравнение 1-го порядка.
Линейное дифференциальное уравнение 1-го порядка. - раздел Математика, Математический анализ Пример. Разберем Пример: ...
Пример. Разберем пример: 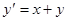 .
.
Решим сначала вспомогательное уравнение 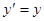 . Это – уже знакомое уравнение с разделяющимися переменными, имеющее решение
. Это – уже знакомое уравнение с разделяющимися переменными, имеющее решение  . Для нахождения решения исходного уравнения используем метод вариации постоянной. Он состоит в следующем. Ищем решение нашего уравнения в виде:
. Для нахождения решения исходного уравнения используем метод вариации постоянной. Он состоит в следующем. Ищем решение нашего уравнения в виде:  , где
, где 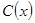 - некоторая дифференцируемая функция. Тогда
- некоторая дифференцируемая функция. Тогда 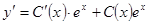 и, подставляя в уравнение, получаем:
и, подставляя в уравнение, получаем:  или
или 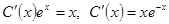 . Интегрируя, находим:
. Интегрируя, находим: 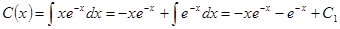 . Тогда
. Тогда 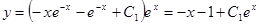 . Итак, мы нашли решение исходного уравнения. Других решений у него нет, поскольку выполнены все условия теоремы о существовании и единственности решения задачи Коши (
. Итак, мы нашли решение исходного уравнения. Других решений у него нет, поскольку выполнены все условия теоремы о существовании и единственности решения задачи Коши (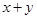 - непрерывная функция от
- непрерывная функция от 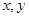 , а ее производная по
, а ее производная по 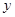 , равная 1, тоже).
, равная 1, тоже).
В общем случае уравнения 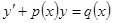 , где
, где  - непрерывные на
- непрерывные на 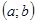 функции мы поступаем вполне аналогично. Сначала решаем вспомогательное однородное уравнение:
функции мы поступаем вполне аналогично. Сначала решаем вспомогательное однородное уравнение: 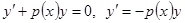 ,
, 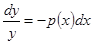 (мы не рассматриваем решение
(мы не рассматриваем решение 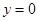 ), откуда, обозначая
), откуда, обозначая 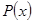 любую первообразную для функции
любую первообразную для функции 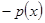 , находим, ограничиваясь случаем
, находим, ограничиваясь случаем 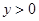 , для определенности,
, для определенности, 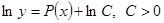 , или
, или 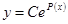 . Далее используем метод вариации постоянных: ищем решение неоднородного уравнения в виде
. Далее используем метод вариации постоянных: ищем решение неоднородного уравнения в виде 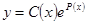 . При этом
. При этом 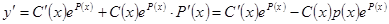 . Подстановка в уравнение дает
. Подстановка в уравнение дает 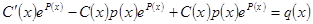 или
или 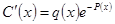 . Интегрируем и, обозначая
. Интегрируем и, обозначая  первообразную для
первообразную для 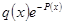 , получаем
, получаем  . Тогда
. Тогда  . Эту формулу иногда записывают в виде
. Эту формулу иногда записывают в виде  , понимая под знаком интеграла не все множество первообразных, а одну произвольно выбранную первообразную.
, понимая под знаком интеграла не все множество первообразных, а одну произвольно выбранную первообразную.
Уравнения, не разрешенные относительно производной. Общее уравнение первого порядка  можно пытаться решать разными методами.
можно пытаться решать разными методами.
Во-первых, можно попытаться все-таки его решить и свести исходное уравнение к одному или нескольким уравнениям вида  .
.
Например, 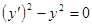 . Уравнение, после преобразования к виду
. Уравнение, после преобразования к виду 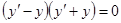 даст равносильную ему совокупность
даст равносильную ему совокупность 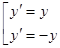 , откуда
, откуда  .
.
Другой способ – введение параметра.
Например, уравнение 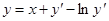 можно решить так: введем параметр
можно решить так: введем параметр 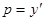 . Тогда
. Тогда 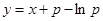 , откуда
, откуда 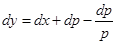 . Но
. Но 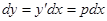 и мы приходим к уравнению
и мы приходим к уравнению 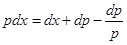 или
или  . При
. При 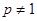 из этого уравнения получаем
из этого уравнения получаем  . Тогда
. Тогда 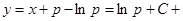
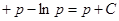 и мы получаем параметрические уравнения:
и мы получаем параметрические уравнения:  . В этом случае параметр
. В этом случае параметр  удается исключить:
удается исключить: 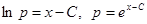 и
и  - явное решение. В случае
- явное решение. В случае 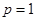 из
из 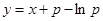 получаем
получаем  .
.
Указанный прием применим к уравнениям Лагранжа и Клеро.
Уравнение Лагранжа имеет вид  , где
, где 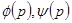 - дифференцируемые функции. Полагая
- дифференцируемые функции. Полагая 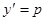 , получаем
, получаем 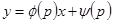 . Дифференцируя, получаем:
. Дифференцируя, получаем:  или
или 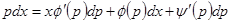 , откуда
, откуда 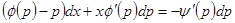 . Предполагая, что
. Предполагая, что 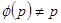 , получаем уравнение
, получаем уравнение 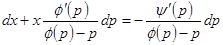 , линейное относительно
, линейное относительно 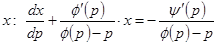 . Решаем его указанным выше методом и получаем выражение для
. Решаем его указанным выше методом и получаем выражение для  через
через  и произвольную постоянную
и произвольную постоянную 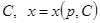 . Тогда
. Тогда 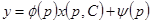 .
.
Уравнение Клеро – это частный случай уравнения Лагранжа: 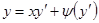 . Вводя параметр
. Вводя параметр 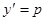 , получаем
, получаем  (т.е.
(т.е. 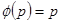 , как раз оставшийся случай),
, как раз оставшийся случай), 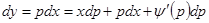 или
или  . Тогда, если
. Тогда, если 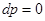 , то
, то 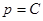 и
и 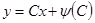 - это общее решение уравнения Клеро. Если же
- это общее решение уравнения Клеро. Если же  , то
, то 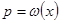 . Тогда
. Тогда 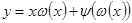 .
.
13. Дифференциальное уравнение n-ного порядка. Задача Коши для уравнения 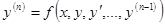 . Понижение порядка дифференциального уравнения
. Понижение порядка дифференциального уравнения
Теорема. Пусть функция 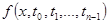 определена и непрерывна в области
определена и непрерывна в области 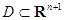 . Пусть
. Пусть  непрерывны в
непрерывны в 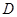 . Тогда задача Коши, состоящая в нахождении решения уравнения
. Тогда задача Коши, состоящая в нахождении решения уравнения 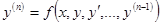 с начальными условиями
с начальными условиями 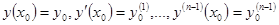 (где точки
(где точки 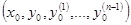 принадлежат области
принадлежат области 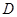 ) имеет, притом единственное, непродолжаемое (максимальное) решение.
) имеет, притом единственное, непродолжаемое (максимальное) решение.
Теорема сформулирована без доказательства.
Методы понижения порядка уравнения. Существуют разные методы снижения порядка (и, тем самым, некоторого упрощения) уравнения. Мы изложим здесь самые простые.
Если уравнение имеет вид 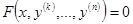 (т.е. не содержит
(т.е. не содержит  , то введение новой переменной
, то введение новой переменной 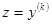 уменьшит порядок уравнения, которое примет вид
уменьшит порядок уравнения, которое примет вид 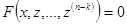 . Если удастся решить это уравнение, то
. Если удастся решить это уравнение, то 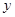 затем можно получить последовательным интегрированием
затем можно получить последовательным интегрированием 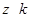 раз.
раз.
Если уравнение не содержит  , т.е. имеет вид
, т.е. имеет вид  , то его порядок можно понизить, взяв
, то его порядок можно понизить, взяв 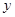 за независимую переменную и считая производную
за независимую переменную и считая производную 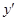 функцией от
функцией от 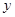 . Поясним это на примере.
. Поясним это на примере.
Пример. Решить уравнение  . Пусть
. Пусть 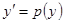 . Тогда
. Тогда 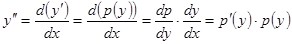 , откуда
, откуда  ;
; 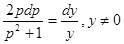 (пусть
(пусть 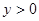 );
);  ;
; 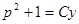 ;
; 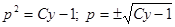 . Таким образом,
. Таким образом,  . Далее находим:
. Далее находим: 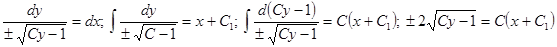 ;
;  .
.
– Конец работы –
Эта тема принадлежит разделу:
Математический анализ
На сайте allrefs.net читайте: "Математический анализ"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейное дифференциальное уравнение 1-го порядка.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов