рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Фундаментальная система решений линейного однородного уравнения
Реферат Курсовая Конспект
Фундаментальная система решений линейного однородного уравнения
Фундаментальная система решений линейного однородного уравнения - раздел Математика, Математический анализ Определение. Любые ...
Определение. Любые  линейно независимых решений линейного однородного дифференциального уравнения
линейно независимых решений линейного однородного дифференциального уравнения  -ного порядка называется фундаментальной системой решений этого уравнения.
-ного порядка называется фундаментальной системой решений этого уравнения.
Из предыдущих теорем сразу следует еще одна важная теорема.
Теорема 7. Решения 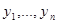 уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского
уравнения (2) образуют фундаментальную систему решений этого уравнения тогда и только тогда, когда их определитель Вронского 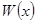 отличен от 0 хотя бы в одной точке
отличен от 0 хотя бы в одной точке 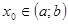 .
.
Доказательство. Равносильная переформулировка утверждения теоремы – решения 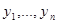 линейно зависимы тогда и только тогда, когда
линейно зависимы тогда и только тогда, когда 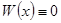 на
на 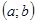 . Но это утверждение сразу следует из теорем 5 и 6.
. Но это утверждение сразу следует из теорем 5 и 6.
Теорема 8. Для любого линейного однородного дифференциального уравнения (2) существует фундаментальная система его решений.
Доказательство. Построим такую фундаментальную систему решений. Для этого возьмем произвольную точку 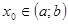 и поставим
и поставим  различных задач Коши:
различных задач Коши:  .
.
По теореме 1 о существовании и единственности у каждой из этих задач имеется решение, и мы обозначим  - решение 1-й задачи,
- решение 1-й задачи,  - решение 2-й задачи, …,
- решение 2-й задачи, …, 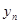 - решение
- решение  -ной задачи. Мы получили
-ной задачи. Мы получили 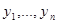 - решения уравнения (2). Найдем
- решения уравнения (2). Найдем 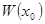 для этих функций:
для этих функций: 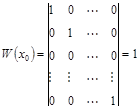 . Следовательно, по теореме 7, функции
. Следовательно, по теореме 7, функции 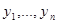 образуют искомую фундаментальную систему решений уравнения (2).
образуют искомую фундаментальную систему решений уравнения (2).
Теорема 9. Пусть 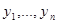 - фундаментальная система решений уравнения (2). Тогда для любого решения
- фундаментальная система решений уравнения (2). Тогда для любого решения 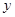 этого уравнения существуют постоянные
этого уравнения существуют постоянные 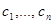 такие, что
такие, что  .
.
Доказательство. Возьмем произвольную точку 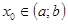 и рассмотрим систему уравнений относительно неизвестных
и рассмотрим систему уравнений относительно неизвестных 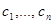 :
: 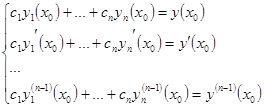 (11). Определитель этой системы
(11). Определитель этой системы 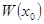 не равен 0, т.к.
не равен 0, т.к. 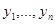 - фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение
- фундаментальная система решений. Поэтому у нее существует (и притом единственное) решение 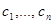 . Рассмотрим теперь функцию
. Рассмотрим теперь функцию  . По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка
. По теореме 2 она является решением уравнения (2). Ввиду равенств (11) значения этой функции и ее производных до порядка  включительно в точке
включительно в точке 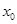 совпадают со значениями
совпадают со значениями 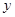 и ее последовательных производных в точке
и ее последовательных производных в точке 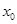 . По теореме 1 о единственности решения задачи Коши
. По теореме 1 о единственности решения задачи Коши  ,
, 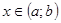 .
.
Замечание. Теоремы 8 и 9 означают, что размерность векторного пространства решений уравнения (2) равна  , а любая фундаментальная система решений представляет собой базис этого пространства.
, а любая фундаментальная система решений представляет собой базис этого пространства.
– Конец работы –
Эта тема принадлежит разделу:
Математический анализ
На сайте allrefs.net читайте: "Математический анализ"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Фундаментальная система решений линейного однородного уравнения
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов