Основные теоремы о дифференцируемых функциях

Теорема Ферма. Пусть функция f(x) определена, непрерывна на интервале (a, b) и в некоторой точке x₀ этого интервала принимает свое наибольшее или наименьшее значение. Если в точке x₀ существует производная этой функции, то 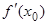= 0.

Доказательство. Пусть f(x₀) = M – наибольшее значение функции на (a, b). Покажем, что f'(x₀) = 0. По определению производной

= .

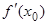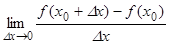Так как f(x₀) – наибольшее значение, то при любом знаке Dx имеем
f(x₀ + Dx) – f(x₀) £ 0. Отсюда, если Dx > 0, то 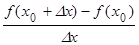£ 0, а поэтому
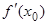£ 0 (см. глава 1).

Если Dx < 0, то 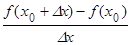³ 0, поэтому 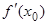³ 0. Так как – определенное число, то получаем, что = 0. Теорема доказана.

Геометрически теорему Ферма поясняет рис. 2.7. В точке x₁ функция принимает наибольшее значение M, а в точке x₂ – наименьшее значение m, касательные к графику y = f (x) в точках A и B параллельны оси Ox, так как f'(x₁) = 0 и f'(x₂) = 0.

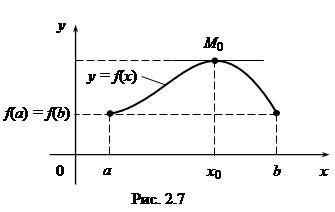Теорема Ролля. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема в каждой внутренней точке и f(a) = f(b), то существует, по крайней мере, одна внутренняя точка x₀ отрезка [a, b], что f'(x₀) = 0.

Доказательство. Так как функция непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и своего наименьшего значения m (см. главу 1)

Если M = m, то функция f(x) постоянна на отрезке [a, b], а потому f'(x) = 0 для любого x Î (a, b).

Рассмотрим случай, когда M ¹ m. Так как f(a) = f(b), то либо M ¹ f(a), либо
m ¹ f(a), тогда либо наибольшее значение M, либо наименьшее значение m достигается во внутренней точке x₀, x₀Î(a, b). Следовательно, по теореме Ферма 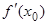= 0. Теорема доказана.

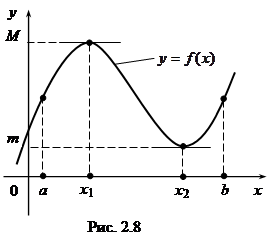
Геометрически теорема Ролля утверждает (рис. 2.8), что если функция непрерывная на [a, b] и дифференцируемая на (a, b), имеет на концах отрезка [a, b] одинаковые значения, то найдется точка x₀ Î (a, b), для которой касательная к графику параллельна оси абсцисс.

Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется хотя бы одна внутренняя точка x₀ отрезка
[a, b], такая, что

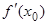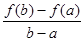=. . (2.14)

Доказательство. Рассмотрим вспомогательную функцию:

F(x) = f(x) – 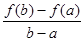(x – a)

и покажем, что она удовлетворяет условиям теоремы Ролля. Функция F(x) непрерывна на [a, b], так как на [a, b] непрерывны функции f(x) и (x – a). Производная

F'(x) = 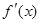– 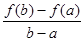(2.15)

существует в интервале (a, b). Вычислим F(x) на концах отрезка [a, b]:

F(a) = f(a) – 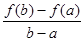(a – a) = f(a),

F(b) = f(b) – 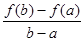(b – a) = f(b) – f(b) + f(a) = f(a).

Значит, F(a) = F(b). По теореме Ролля найдется точка x₀ Î (a, b), такая, что
F'(x₀) = 0. Подставив x₀ в равенство (2.15) получи F'(x₀) = 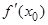– 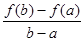, откуда = .

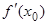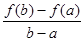Теорема доказана.

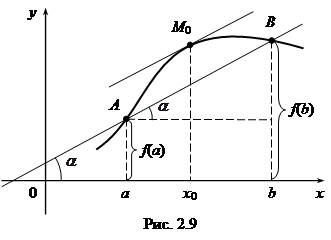
Поясним теорему Лагранжа геометрически (рис. 2.9).

Отношение 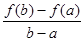есть угловой коэффициент tga хорды AB, соединяющей точки A(a, f(a)), B(b, f(b)), f'(x₀) – угловой коэффициент касательной к графику y = f(x), проведенной в точке M₀(x₀, f(x₀)), и 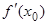= tga. Теорема Лагранжа утверждает, что на графике функции y = f(x) найдется хотя бы одна точка M₀, в которой касательная к графику параллельна хорде AB.

Заметим, что формулу (2.14) можно записать в виде:

f(b) – f(a) = 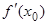(b – a). (2.16)

Обозначив x₀ = c, a = x₀, b – a = Dx, b = x₀ + Dx, из формулы (2.16) получаем формулу:

f(x₀ + D x) – f(x₀) = (c)Dx. (2.17)

Формулы (2.16), (2.17) называют формулами конечных приращений, а теорему Лагранжа – теоремой о конечных приращениях. При этом теорема Лагранжа переформулируется следующим образом: приращение дифференцируемой функции на отрезке равно произведению длины отрезка на значение производной этой функции в некоторой внутренней точке отрезка.

Получим следствие из теоремы Лагранжа. Известно, что производная постоянной функции равна нулю. Докажем обратное утверждение.

Следствие. Если функция f(x) непрерывна на отрезке [a, b] и во всех внутренних точках этого отрезка (x) = 0, то функция f(x) постоянна на отрезке [a, b].

Доказательство. Пусть x – произвольная точка отрезка [a, b], не совпадающая с a, тогда по формуле (2.16) конечных приращений применительно к отрезку [a, x] имеем: f(x) – f(a) = (x₀)(x – a), где x₀ Î (a, x). Но (x₀) = 0, поэтому f(x) = f(a).

Следовательно, "x Î [a, b]: f(x) = f(a) и f(x) – постоянна на [a, b].

Теорема Коши. Пусть функции f(x), g(x) непрерывны на отрезке [a, b], дифференцируемы на (a, b), причем g'(x) ¹ 0 для любой точки x из интервала (a, b). Тогда существует внутренняя точка x₀ отрезка [a, b], такая, что

=.

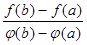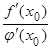Доказательство. Отметим, что j(b) ¹ j(a), так как в противном случае по теореме Ролля j'(x) = 0 в некоторой точке x₀Î(a, b).

Введем вспомогательную функцию: F(x) = f(x) – 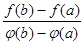(j(x) – j(a)) и покажем, что F(x) удовлетворяет теореме Ролля. Очевидно, что F(x) непрерывна на отрезке [a, b], дифференцируема на (a, b) и F'(x) = f'(x) –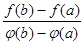 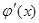, и на концах отрезка [a, b] имеет равные значения: F(a) = f (a), F(b) = f (a).

Следовательно, по теореме Ролля найдется точка x₀Î(a, b) такая, что F'(x₀) = 0:

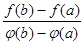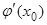F'(x₀) = (x₀) – ×= 0.

Отсюда 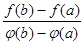=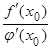. Теорема доказана.

Теоремы Ферма, Ролля, Лагранжа, Коши будут многократно применяться на протяжении курса математического анализа.