Экстремумы функции

Дадим точные определения точкам максимума и минимума функции. Пусть функция f(x) определена на промежутке X и x₀ Î X.

Говорят, что в точке x₀ функция f(x) имеет максимум, если существует такая окрестность точки x₀, что для любого x из этой окрестности f(x) < f(x₀).

Точка x₀ называется точкой минимума, если существует такая окрестность точки x₀, что для любого x из этой окрестности f(x) > f(x₀).

Точки максимума и минимума называются точками экстремума.

Замечание. Точки экстремума всегда являются внутренними точками промежутка, т.е. не могут быть его концом.

Теорема 1. (Необходимое условие экстремума)

Если функция f(x) дифференцируема в точке x₀ и некоторой ее окрестности и
x₀ – точка экстремума, то (x₀) = 0.

Доказательство. Пусть для определенности x₀ – точка максимума, тогда найдется окрестность (x₀ – d, x₀ + d) точки x₀ такая что, для любого xÎ(x₀ – d, x₀ + d)
f(x) < f(x₀), т.е. f(x₀) – наибольшее значение функции f(x) на интервале (x₀ – d, x₀ + d). Тогда по теореме Ферма (разд. 2.9) (x₀) = 0. Теорема доказана.

Следствие. Если x₀ – точка экстремума, то (x₀) = 0 или (x₀) не существует.

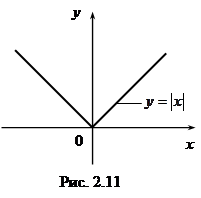
В качестве примера приведем функцию f(x) = |x| (рис. 2.11).

Очевидно, что x₀ = 0 является точкой минимума, так как |0| < |x| для любого x ¹ 0. А в точке x₀ = 0 производной f'(0) не существует.

 

 

Если f'(x₀) = 0 или f'(x₀) не существует, то точку x₀ будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.

Теорема 2. (Первое достаточное условие экстремума)

Пусть функция f (x) определена и непрерывна в точке x₀ и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, может быть, точки x₀, и x₀ – критическая точка для функции f (x) (т.е. (x₀) = 0 или (x₀) не существует). Тогда: 1) если при x < x₀ производная (x) > 0, а для x > x₀: (x) < 0, то x₀ – точка максимума; 2) если при x < x₀: (x) < 0, а при x > x₀: (x) > 0, то x₀ – точка минимума.

Доказательство. Пусть для x < x₀: (x) > 0, а для x > x₀: (x) < 0, т.е. при переходе через точку x₀ слева направо производная меняет знак с + на –. Тогда слева от x₀ функция f(x) возрастает, а справа от x₀ функция f(x) убывает, следовательно, x₀ – точка максимума. Аналогично доказывается вторая часть теоремы.

Теорема 3. (Второе достаточное условие экстремума).

Пусть функция f (x) дважды дифференцируема в точке x₀ и некоторой ее окрестности и пусть (x₀) = 0. Если (x₀) > 0, то x₀ – точка минимума. Если (x₀) < 0, то x₀ – точка максимума.

Доказательство. Пусть (x₀) = 0 и (x₀) > 0. Покажем, что x₀ – точка минимума:

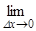
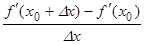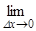
f''(x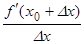₀) = = > 0.

Тогда в некоторой окрестности точки x₀ выполняется неравенство
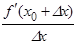> 0. Отсюда, если Dx < 0, то (x₀ + Dx) < 0, а если Dx > 0, то (x₀ + Dx) > 0, т.е. слева от точки x₀ функция f(x) убывает, а справа – возрастает, это означает, что
x₀ – точка минимума. Аналогично доказывается вторая часть теоремы для (x₀) < 0.

При исследовании функции на монотонность и экстремумы бывает удобно результаты заносить в таблицу. Как это делается, покажем в следующем примере.

Пример 1. Исследовать на монотонность и экстремумы функцию f(x) = x²e^–x. Построить ее график.

Решение. Эта функция определена и непрерывна на всей числовой оси (–¥, ¥). Найдем производную: (x) = 2xe^–x – x²e^–x = xe^–x(2 – x). Тогда (x) = 0 при x₁ = 0 и
x₂ = 2, где x1, x₂ – критические точки. Эти точки разбивают всю числовую ось на три интервала: (–¥; 0), (0; 2), (2; +¥). Составим таблицу, в первой строке которой поместим указанные точки и интервалы, во второй строчке – сведения о производной (x) в точках и на интервалах, а в третьей – поведение данной функции f(x):

 

x		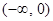x1 = 0	(0, 2)	x2 = 0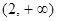
(x)	(x) < 0		(x) > 0		(x) < 0
f(x)	убывает		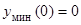возрастает		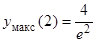убывает

 

Определим знак (x) на каждом из интервалов: если xÎ(–¥, 0), то (x) < 0; если xÎ(0, 2), то (x)>0; если xÎ(2, +¥), то (x) < 0. Отсюда определяется поведение функции f(x): на первом и последнем интервалах f(x) убывает, а на втором – возрастает. Отсюда следует, что x₁ = 0 является точкой минимума, y_мин(0) = 0, а x₂ = 2 – точка максимума, y_макс(2) =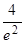» 0,54. Для построения графика заметим, что f (x) > 0 для всех x, отличных от нуля, и

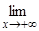x²e^–x = 0,

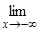x²e^–x = ¥, f(–1) = e » 2,7.

График этой функции изображен на рис. 2.12.

Отметим, что дальнейшее исследование этой функции (см. следующий раздел) позволит уточнить ее график.

Пример 2. Исследовать на экстремум функцию f (x) = x + .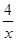

Решение. Область определения функции (-¥, 0)È(0, +¥), в каждом из этих интервалов функция непрерывна. Найдем f'(x) и f''`(x): f `(x) = 1 – 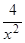, f''(x) = 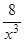. Теперь найдем критические точки функции, для этого решим уравнение f'(x) = 0:
1 – 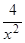= 0, отсюда x₁ = –2, x₂ = +2 – критические точки. Используем теорему 3 для исследования критических точек, для этого вычислим f''(x) в точках x₁ и x₂. Так как
f''(–2) = 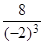= –1< 0, то x₁ = –2 является точкой максимума f_макс(–2) = –2 – 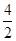= –4. Для x₂: f''(2) = 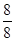= 1 > 0, поэтому x₂ = 2 – точка минимума, f_мин(2) = 2 + 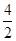= 4.

Таким образом, функция f(x) = x + 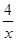имеет максимум при x₁ = –2, f(–2) = –4 и имеет минимум при x₂ = 2, f(2) = 4.

Известно, что если функция непрерывна на отрезке, то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения (см. гл. 1). Иногда требуется найти наименьшее или наибольшее значение такой функции.

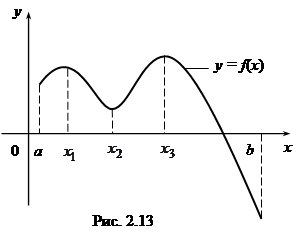
Если на отрезке [a, b] есть точки минимума и максимума функции f(x) (рис. 2.13), то наименьшее значение функция будет принимать либо в одной из точек минимума, либо на конце отрезка [a, b]. Аналогично для наибольшего значения.

Алгоритм нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке:

· найти критические точки x₁, x₂, ..., x_n функции f(x), принадлежащие отрезку ;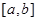

· вычислить значения функции f (x) в критических точках и на концах отрезка;

· из этих значений выбрать самое большое и самое малое, эти числа и будут наибольшим и наименьшим значениями f(x) на отрезке [a, b].

Пример 3. Найти наименьшее и наибольшее значения функции:

f(x) = x⁴ – 2x² + 5 на отрезке [–2, 2].

Решение. Найдем критические точки для данной функции:

(x) = 4x³ – 4x = 4x(x² – 1);

(x) = 0 при x₁ = 0, x₂ = –1, x₃ = +1, все три критические точки принадлежат данному отрезку. Вычислим значения функции в точках –2, –1, 0, 1, 2:

f(–2) = (–2)⁴ – 2×(–2)² + 5 = 16 – 8 + 5 = 13, f(–1) = 1 – 2 + 5 = 4,
f(0) = 5, f(1) = 4, f(2) =13.

Из найденных значений самое малое число 4, а самое большое число 13.

Итак, наименьшее значение функции равно 4, наибольшее значение равно 13.