Выпуклость, вогнутость графика функции, точки перегиба

Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x).

Кривая, заданная функцией y = f(x), называется выпуклой на интервале (a, b), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая называется вогнутой на интервале (a, b), если все точки кривой лежат выше любой ее касательной на этом интервале.

Точка кривой M₀(x₀, f(x₀)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.

Кривая y = f(x) (рис. 2.14) является выпуклой на интервалах (–2; –1,5) и (0; 1,5), вогнутой на интервалах (–1,5; 0) и (1,5; 2). Точки M₁(–1,5; f(–1,5)), O(0, 0),
M₂(1,5; f(1,5)) – точки перегиба.

Теорема 1. (Достаточные условия выпуклости и вогнутости графика функции).

Если во всех точках интервала (a, b) вторая производная функции f(x) отрицательна, т.е. f''(x) < 0, то кривая y = f(x) на этом интервале выпукла.

Если во всех точках интервала (a, b): 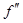(x) > 0, то кривая y = f(x) на этом интервале вогнута.

Доказательство. 1) Пусть 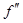(x) < 0 для xÎ(a, b). Возьмем на интервале (a, b) произвольную точку x₀ и проведем касательную M₀K к кривой y = f(x) в точке M₀(x₀, f(x₀)) (см. рис. 2.15).

Покажем, что все точки кривой y = f(x) лежат ниже точек касательной M₀K (за исключением общей точки M₀), т.е. при одном и том же значении x ордината y = f(x) кривой меньше ординаты касательной:

y_кас = f(x₀) + (x₀)(x – x₀)

(об уравнении касательной см. разд. 2.1). Покажем, что y – y_кас< 0. Действительно,

y – y_кас = f(x) – f(x₀) – (x₀)(x – x₀).

Применим к разности f(x) – f(x₀) теорему Лагранжа:

f(x) – f(x₀) = (с)(x – x₀),

где c лежит между x и x₀, тогда

y – y_кас = (с)(x – x₀) – (x₀)(x – x₀) = ((c) – (x₀))(x – x₀).

К разности f'(c) – f'(x₀) опять применим теорему Лагранжа:

(c) – (x₀) = 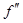(c₁)(c – x₀),

где c₁ лежит между x₀ и c, тогда

y – y_кас = 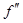(c₁)(c – x₀)(x – x₀).

Определим знак разности y – y_кас. По условию 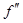(c₁) < 0. Покажем, что
(c – x₀)(x – x₀) > 0. Действительно, если x > x₀, то c > x₀ (так как c лежит между x и x₀), следовательно, в этом случае (c – x₀)(x – x₀) > 0. Если x < x₀, то c < x₀, то опять
(c – x₀)(x – x₀) > 0. Значит, y – y_кас < 0, т.е. y < y_кас.

Вторая часть теоремы доказывается аналогично.

Теорема 2 (достаточное условие точки перегиба)

Пусть кривая является графиком функции y = f(x). Если 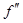(x₀) = 0 или 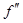(x₀) не существует и при переходе через x₀ вторая производная 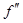(x) меняет свой знак, то точка M₀(x₀, f(x₀)) этой кривой является точкой перегиба.

Доказательство. Пусть для x < x₀: 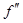(x) < 0, а для x > x₀: 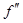(x) > 0, тогда слева от точки M₀(x₀, f(x₀)) график функции y = f(x) выпуклый, а справа от M₀ – вогнутый, т.е. M₀ – точка перегиба.

Пример. Исследовать на выпуклость, вогнутость и точки перегиба график функции y = x²e^–x (см. разд. 2.13).

Решение

f(x) = x²e^–x, f'(x) = 2xe^–x – x²e^–x, f''(x) =
= 2e^–x – 2xe^–x – 2xe^–x + x²e^–x = e^–x(2 – 4x + x²).

Найдем значения x, при которых 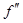(x) = 0 и интервалы знакопостоянства второй производной 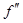(x):

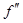(x) = 0, 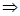e^-x(2 - 4x + x²) = 0,

Корни этого уравнения:

x₁= 2 – 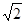» 0,58 и x₂ = 2 + 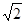» 3,41.

Значения функции f (x) в точках x₁, x₂:

y₁ = f(x₁) » 0,34 и y₂ = f(x₂) » 0,38.

Результаты исследования занесем в таблицу:

 

x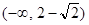
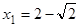
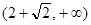
f»(x)	f»(x) > 0	f»(x1) = 0	f»(x) < 0	f»(x2) = 0	f»(x) > 0
f(x)	Кривая вогнутая	M1(x1, y1) – точка перегиба	Кривая выпуклая	M2(x2, y2) – точка перегиба	Кривая вогнутая

 

Построим график функции y = x²e^–x рис. (2.16) с учетом исследования примера 1 (разд.2.13)