рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование

Реферат Курсовая Конспект

Выберите учебное заведение

Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование

Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование - раздел Математика, ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ Пусть Переменные X, Y Связаны Между Собой Некоторым Уравнением ...

Пусть переменные x, y связаны между собой некоторым уравнением

F(x, y) = 0, (2.1)

причем y является функцией от x, тогда говорят, что функция y задана неявно уравнением (2.1).

Например, уравнение y³– 5x²– 3x = 0 задает неявно функцию y, которую можно из этого уравнения выразить через x явно: y = .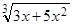

Уравнение x²+ y²= a² неявно задает две функции:

y = и y = –.

Однако не всегда, функции, заданные неявно могут быть выражены явно через элементарные функции. Так, из уравнения y + x = 2siny, которое неявно задает функцию y, нельзя выразить y явно через элементарные функции.

Как найти y' для функции, заданной неявно, уравнением (2.1)? Для этого надо найти производные по x от обеих частей этого уравнения, помня, что y – функция от x и приравнять эти производные. Из полученного уравнения найти y'.

Например, найдем y' для функции, заданной неявно уравнением x²+ y²= a²:

(x²+ y²= (a², 2x + 2y×y' = 0,

отсюда y' = –.

Применим этот метод для нахождения производной для показательно-степенной функции y = u(x)^v^(x), где u(x) > 0, u(x), v(x) – дифференцируемые функции.

Прологарифмируем равенство y = u^v, получим: lny = v×lnu. Дифференцируем полученное равенство: 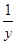y' = v'×lnu + v×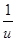×u', откуда y' = y(v'×lnu + v×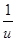×u'), подставляя сюда y = u^v, имеем: y' = u^v×lnu×v'+ v×u^v–¹×u'.

Этот прием нахождения производной называется логарифмическим дифференцированием.

Пример. y = x^sinx, (x > 0). Найти y'.

Решение.lny = sinx×lnx, (lny)' = (sinx×lnx)', 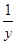×y' = cosx×lnx + sinx×,
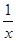y' = x^sinx(cosx×lnx + sinx×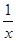) или y' = x^sinxcosx×lnx + sinx×x^{sinx – 1}.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Основные правила дифференцирования... Установим правила по которым можно находить производные суммы произведения... Теорема Если функции u x v x дифференцируемы в точке x то их сумма дифференцируема в этой точке причем...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Дифференцирование функций, заданных неявно. Логарифмическое дифференцирование

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Понятие производной, ее геометрический и механический смысл
Пусть функция y = f (x) определена в точке x0 и некоторой ее окрестности, x – точка из этой окрестности. Введем обозначения: разность x – x0

Решение
Если

Производные некоторых элементарных функций
Пусть функция y = f (x) определена на некотором промежутке X, x0ÎX и f(x) дифференцируема в точке x0, т.е. произв

Доказательство
Так как Du = u(x + Dx) – u(x), то u(x + Dx) = u(x) + Du.

Производные обратных тригонометрических и гиперболических функций
Используя теорему 5 (разд. 2.3) докажем следующие формулы: 1) ; 2)

Функции, заданные параметрически, и их дифференцирование
Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

Дифференциал функции
Пусть функция в точке x0 имеет производную. По определению: =

Решение
1) Dy = (x + Dx)2 – x2 = x2 + 2xDx + (Dx)2 – x2 = 2xDx + (Dx)2

Производные и дифференциалы высших порядков
Пусть функция f(x) определена и дифференцируема на некотором промежутке X, тогда ее производная (x) та

Основные теоремы о дифференцируемых функциях
Теорема Ферма. Пусть функция f(x) определена, непрерывна на интервале (a, b) и в некоторой точке x0 этого интервала принимает свое наи

Правило Лопиталя
В главе 1 мы познакомились с приемами нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа

Формула Тейлора
Формула Тейлора является одной из важнейших формул математического анализа, она имеет очень большое число теоретических и практических применений. Рассмотрим предварительно следующую задач

Возрастание и убывание функций
Теорема 1. (Достаточное условие возрастания функции) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (

Экстремумы функции
Дадим точные определения точкам максимума и минимума функции. Пусть функция f(x) определена на промежутке X и x0 Î X. Говорят, что в точ

Выпуклость, вогнутость графика функции, точки перегиба
Пусть f(x) – функция, дифференцируемая на интервале (a, b). Рассмотрим кривую, являющуюся графиком функции y = f(x). Кривая, заданная функцией

Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а, значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки