рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность.
Реферат Курсовая Конспект
Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность.
Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность. - раздел Математика, Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства Пусть Дана Система Векторов (1) ...
Пусть дана система векторов (1)  ,
, 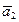 , …,
, …, 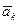 из векторного пространства V над полем Р.
из векторного пространства V над полем Р.
Определение 1. Максимальная линейно независимая подсистема системы векторов (1) называется базисом этой системы.
Теорема. Если система (2)  ,
, 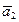 , …,
, …,  — базис системы векторов (1), то любой вектор системы векторов (1) является линейной комбинацией системы векторов (2), причем такое представление (разложение по базису) единственно.
— базис системы векторов (1), то любой вектор системы векторов (1) является линейной комбинацией системы векторов (2), причем такое представление (разложение по базису) единственно.
Доказательство. Пусть  — некоторый вектор из системы векторов (1). Если
— некоторый вектор из системы векторов (1). Если  принадлежит базису (2), то
принадлежит базису (2), то  =
=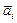 для некоторого iÎ{
для некоторого iÎ{ }. Тогда
}. Тогда  = 0
= 0 + … + 1
+ … + 1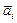 + … + 0
+ … + 0 — разложение вектора
— разложение вектора  по базису (2). Если
по базису (2). Если  не принадлежит базису (2), то рассмотрим систему векторов
не принадлежит базису (2), то рассмотрим систему векторов
(3)  ,
, 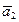 , …,
, …,  ,
,  .
.
По определению базиса, система векторов (3) является линейно зависимой. Это означает, что существуют скаляры a1, a2,..., ar, ar+1 принадлежащие полю Р и не равные нулю одновременно такие, что выполняется равенство (4) a1 + a2
+ a2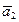 + … + ar
+ … + ar + ar+1
+ ar+1 =
=  . Допустим, что ar+1=0. Тогда ar+1
. Допустим, что ar+1=0. Тогда ar+1 =
= и a1
и a1 + a2
+ a2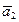 + … + ar
+ … + ar + ar+1
+ ar+1 =
=  , причём скаляры a1, a2,..., ar не равны нулю одновременно. Это означает, что система векторов (2) линейно зависима. Получили противоречие с определением базиса. Поэтому ar+1¹0. Выразим вектор
, причём скаляры a1, a2,..., ar не равны нулю одновременно. Это означает, что система векторов (2) линейно зависима. Получили противоречие с определением базиса. Поэтому ar+1¹0. Выразим вектор  из равенства (4). Получим
из равенства (4). Получим
 = -
= - 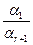
 -
- 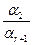
 - … -
- … - 
 ,
,
то есть вектор  является линейной комбинацией базисных векторов (2).
является линейной комбинацией базисных векторов (2).
Покажем, что такое представление единственно. Допустим, что существуют два представления вектора  в виде линейной комбинации базисных векторов (2):
в виде линейной комбинации базисных векторов (2):
(5)  = a1
= a1 + a2
+ a2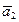 + … + ar
+ … + ar и (6)
и (6)  = b1
= b1 + b2
+ b2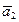 + … + br
+ … + br .
.
Вычтем из равенства (5) равенство (6). Получим (7)  = (a1 - b1)
= (a1 - b1) + (a2 - b2)
+ (a2 - b2)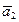 + … + (ar - br)
+ … + (ar - br) . Поскольку система векторов (2) линейно независима, то из равенства (7) следует, что все скаляры ai-bi равны нулю, i=
. Поскольку система векторов (2) линейно независима, то из равенства (7) следует, что все скаляры ai-bi равны нулю, i= . Это означает, что ai=bi для всех i=
. Это означает, что ai=bi для всех i= и представления (5) и (6) совпадают. Таким образом, существует единственное представление вектора
и представления (5) и (6) совпадают. Таким образом, существует единственное представление вектора  в виде линейной комбинации базисных векторов. Теорема доказана.
в виде линейной комбинации базисных векторов. Теорема доказана.
Определение 2. Представление вектора  в виде линейной комбинации базисных векторов
в виде линейной комбинации базисных векторов  ,
, 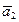 , …,
, …,  называется разложением вектора
называется разложением вектора  по базису
по базису  ,
, 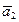 , …,
, …,  :
: = a1
= a1 + a2
+ a2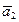 + … + ar
+ … + ar .
.
Кортеж (a1, a2, … , ar) называется координатной вектор-строкой вектора  в базисе (2). Коэффициенты a1, a2, …, ar разложения вектора
в базисе (2). Коэффициенты a1, a2, …, ar разложения вектора  по базису (2) называются координатами вектора
по базису (2) называются координатами вектора  в базисе (2).
в базисе (2).
Замечание.Из доказанной теоремы следует, что координаты единственным образом определяют вектор.
– Конец работы –
Эта тема принадлежит разделу:
Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Определение Матрицей размера m times n над полем Р называется прямоугольная таблица состоящая из n строк и m столбцов следующего вида... где aij P i j... Определение Квадратной матрицей n го порядка над полем P называется матрица размера n times n над полем P...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов