рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Ядерная техника
- /
- Особенности периодической системы элементов
Реферат Курсовая Конспект
Особенности периодической системы элементов
Особенности периодической системы элементов - раздел Ядерная техника, В данной теме мы начнем изучение квантовых закономерностей явлений природы Располагая Химические Элементы В Порядке Возрастания Атомного Веса, Менделеев...
Располагая химические элементы в порядке возрастания атомного веса, Менделееву пришлось отступить от этого исходного принципа и переставить места некоторых элементов, придавая большее значение периодичности химических свойств. Менделееву пришлось ввести понятие порядкового номера элемента  , не понимая точного смысла этого числа.
, не понимая точного смысла этого числа.
Позднее исследования Резерфорда и Мозли показали, что атомный номер равен заряду ядра, измеренному в единицах элементарного заряда. Порядковый номер равен числу протонов в ядре и числу электронов в нейтральном атоме.
Свойства атома определяются состоянием всей электронной оболочки атома и периодическая повторяемость свойств химических элементов является отражением изменений структуры электронной оболочки атома при увеличении числа электронов.
Поскольку задача многих тел в квантовой механике сложна не менее, чем в классической, то отыскание точной волновой функции, описывающей состояние всех электронов в атоме, невозможно методами современной математики. Поэтому для объяснения периодического закона используют приближенное представление о состоянии отдельных электронов в атоме.
При качественном рассмотрении системы электронов в многоэлектронных атомах в нулевом приближении можно положить, что электроны не взаимодействуют друг с другом и находятся в кулоновском поле ядра. В таком приближении волновые функции электронов 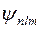 совпадают с волновыми функциями электрона в кулоновском поле ядра с зарядом
совпадают с волновыми функциями электрона в кулоновском поле ядра с зарядом 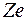 , а энергия электронов определяется главным квантовым числом
, а энергия электронов определяется главным квантовым числом 
 . (1)
. (1)
Таким образом, в таком подходе считается, что электроны в многоэлектронном атоме находятся в одночастичных состояниях, характеризуемых четверкой квантовых чисел «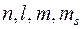 ». Это позволило учесть принцип Паули в самой простейшей его формулировке: в каждом одночастичном состоянии, характеризуемом четверкой квантовых чисел «
». Это позволило учесть принцип Паули в самой простейшей его формулировке: в каждом одночастичном состоянии, характеризуемом четверкой квантовых чисел «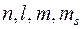 » может находиться только один электрон.
» может находиться только один электрон.
В силу того, что различные одночастичные состояния вырождены, одной энергии такого состояния соответствует  разных состояний, отличающихся величиной орбитального момента и проекциями орбитального и спинового моментов. Все одночастичные состояния с одинаковой энергией образуют электронную оболочку, емкости таких оболочек равны 2, 8, 18, 32, 50, … . число элементов в периодах таблицы Менделеева совпадает с этими числами, но последовательность чисел несколько другая: 2, 8, 8, 18, 18, 32, … .
разных состояний, отличающихся величиной орбитального момента и проекциями орбитального и спинового моментов. Все одночастичные состояния с одинаковой энергией образуют электронную оболочку, емкости таких оболочек равны 2, 8, 18, 32, 50, … . число элементов в периодах таблицы Менделеева совпадает с этими числами, но последовательность чисел несколько другая: 2, 8, 8, 18, 18, 32, … .
Каждая электронная оболочка может быть разбита на подоболочки с различными значениями орбитального квантового числа 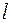 . Емкость подоболочек
. Емкость подоболочек  составляет ряд чисел: 2, 6, 10, 14, … .
составляет ряд чисел: 2, 6, 10, 14, … .
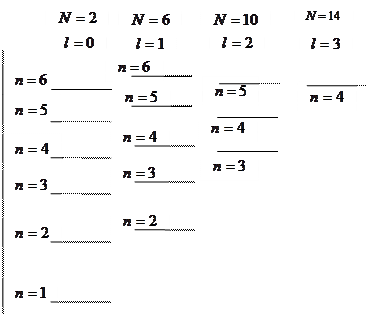 |
Основное (невозбужденное) состояние атома соответствует минимальному значению энергии электронов. Поэтому в соответствии с принципом Паули электроны занимают состояния с наименьшим значением главного квантового числа, а по мере исчерпания емкости соответствующей оболочки остальные электроны размещаются в состояниях с большими значениями главного квантового числа
 .
.
Первый период состоит всего из двух элементов, потому что электроны этих атомов размещаются в оболочке с  , емкость которой равна 2. следует отметить, что расчет энергии ионизации для
, емкость которой равна 2. следует отметить, что расчет энергии ионизации для  по формуле
по формуле  дает значение 54,4 эВ, тогда как измеренное значение составляет 24,45 эВ. Это значит, что для расчета энергии ионизации необходимо учитывать взаимное отталкивание электронов.
дает значение 54,4 эВ, тогда как измеренное значение составляет 24,45 эВ. Это значит, что для расчета энергии ионизации необходимо учитывать взаимное отталкивание электронов.
Второй период таблицы Менделеева содержит восемь химических элементов. Два электрона у этих элементов заполняют оболочку с  , остальные располагаются в состояниях с большей энергией, в которых
, остальные располагаются в состояниях с большей энергией, в которых 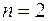 . Эта оболочка состоит из двух подоболочек с
. Эта оболочка состоит из двух подоболочек с 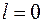 и
и  , емкости которых равны, соответственно, 2 и 6.
, емкости которых равны, соответственно, 2 и 6.
В конце обоих периодов находятся инертные газы  и
и 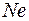 , которым соответствуют заполненные оболочки. Заполненным оболочкам соответствует наибольшая энергия ионизации в соответствующем периоде. При увеличении порядкового номера в периоде энергия ионизации возрастает от наименьшего значения у щелочного металла до наибольшего значения у инертного газа. Так у
, которым соответствуют заполненные оболочки. Заполненным оболочкам соответствует наибольшая энергия ионизации в соответствующем периоде. При увеличении порядкового номера в периоде энергия ионизации возрастает от наименьшего значения у щелочного металла до наибольшего значения у инертного газа. Так у  (
( ) энергия ионизации составляет 5,37 эВ, а у
) энергия ионизации составляет 5,37 эВ, а у 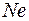 (
( ) энергия ионизации равна 21,48 эВ.
) энергия ионизации равна 21,48 эВ.
Элементы второго и третьего периодов
| Li 5,37 | Be 9,48 | B 8,4 | C 11,217 | N 14,47 | O 13,56 | F 18,6 | Ne 21,48 |
| Na 5,12 | Mg 7,61 | Al 5,96 | Si 7,39 | P 10,3 | S 10,31 | Cl 12,96 | Ar 15,69 |
Химические свойства элементов с увеличением порядкового номера изменяются именно из-за увеличения энергии ионизации. Щелочные металлы легко могут потерять электрон, а галогены (предпоследний элемент в периоде) легко присоединяют электрон.
Для  распределение электронов по оболочкам нельзя объяснить только с помощью принципа Паули. В атомах этих элементов существенное влияние на заполнение электронных оболочек оказывает взаимодействие электронов. В первом приближении его можно учесть, если считать, что каждый электрон движется не только в поле притяжения ядра с зарядом
распределение электронов по оболочкам нельзя объяснить только с помощью принципа Паули. В атомах этих элементов существенное влияние на заполнение электронных оболочек оказывает взаимодействие электронов. В первом приближении его можно учесть, если считать, что каждый электрон движется не только в поле притяжения ядра с зарядом 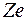 , но и в самосогласованном центральном поле остальных электронов.
, но и в самосогласованном центральном поле остальных электронов.
 |
Учет отталкивания электронов сводится к частичному экранированию ими ядра атома, что приводит к двум эффектам. Прежде всего, все уровни энергии в сравнении с (1) поднимаются за счет замены
 на эффективный заряд ядра
на эффективный заряд ядра 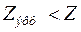 . Кроме того, влияние экранирования по-разному сказывается на электронах, принадлежащих разным подоболочкам (с разными
. Кроме того, влияние экранирования по-разному сказывается на электронах, принадлежащих разным подоболочкам (с разными 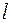 ). Это приводит к тому, что энергия электронов зависит не только от главного квантового числа, но и от орбитального. В результате схема уровней многоэлектронного атома существенно отличается от схемы уровней в атоме водорода. В частности уровень с
). Это приводит к тому, что энергия электронов зависит не только от главного квантового числа, но и от орбитального. В результате схема уровней многоэлектронного атома существенно отличается от схемы уровней в атоме водорода. В частности уровень с 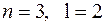 оказывается намного выше уровней с
оказывается намного выше уровней с  и даже чуть выше уровня с
и даже чуть выше уровня с  ,
,  . В многоэлектронном атоме электроны следовало бы распределять по подоболочкам с заданными числами
. В многоэлектронном атоме электроны следовало бы распределять по подоболочкам с заданными числами  и
и 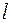 .
.
Если под оболочкой понимать совокупность электронов, занимающих близкие по величине уровни энергии и удаленные от других уровней так, что 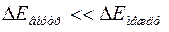 , где
, где  - расстояние между уровнями внутри одной оболочки, а
- расстояние между уровнями внутри одной оболочки, а  - расстояние между уровнями разных оболочек, то первоначальные оболочки расщепляются и частично перепутываются. Поэтому в оболочки, соответствующие четвертому, пятому и шестому периодам входят подоболочки из разных слоев. Не меняются только
- расстояние между уровнями разных оболочек, то первоначальные оболочки расщепляются и частично перепутываются. Поэтому в оболочки, соответствующие четвертому, пятому и шестому периодам входят подоболочки из разных слоев. Не меняются только  и
и 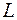 слои. При этом в третью оболочку входят только две подоболочки
слои. При этом в третью оболочку входят только две подоболочки  и
и 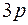 , в четвертую оболочку входят в порядке возрастания энергии
, в четвертую оболочку входят в порядке возрастания энергии  ,
, 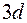 и
и 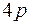 подоболочки, в пятую оболочку входят
подоболочки, в пятую оболочку входят  ,
,  и
и 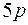 подоболочки, в шестую оболочку входят
подоболочки, в шестую оболочку входят  ,
,  ,
,  и
и 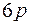 подоболочки, в седьмую оболочку входят
подоболочки, в седьмую оболочку входят  ,
, 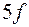 ,
,  .
.
Это приводит к тому, что емкости перестроенных в результате экранировки оболочек уже соответствуют числам элементов в периодах таблицы Менделеева. Удается объяснить и другие особенности расположения элементов в этой таблице.
Электроны атомов первого периода заполняют первую оболочку ( слой). Она состоит из одной подоболочки
слой). Она состоит из одной подоболочки 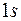 . Два электрона атомов второго периода так же располагаются в первой оболочке. Следующие два электрона заполняют подоболочку
. Два электрона атомов второго периода так же располагаются в первой оболочке. Следующие два электрона заполняют подоболочку  . Энергия этих состояний значительно больше энергии состояний
. Энергия этих состояний значительно больше энергии состояний 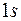 . Остальные электроны атомов этих элементов заполняют оболочку
. Остальные электроны атомов этих элементов заполняют оболочку  , емкость которой равна 6. Энергия этих состояний незначительно превышает энергию состояний
, емкость которой равна 6. Энергия этих состояний незначительно превышает энергию состояний  .
.
У элементов третьего периода 10 электронов располагаются на первых двух оболочках, а остальные электроны этих атомов занимают более высокие энергетические состояния сначала подоболочки  , а затем
, а затем 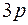 . Третья оболочка почти ничем не отличается от второй оболочки. Поэтому свойства атомов элементов этого периода повторяют свойства атомов второго периода. В приведенной таблице показаны энергии ионизации атомов. Энергия ионизации в обоих периодах возрастает с увеличением порядкового номера (заряда ядра). Это увеличение энергии ионизации связано с увеличением силы притяжения к ядру, в результате чего понижается каждый одночастичный уровень энергии. Но для элементов третьего периода энергия ионизации меньше, чем для соответствующих элементов второго периода, что связано с увеличением главного квантового числа. Соответственно повторяются химические и оптические свойства этих элементов.
. Третья оболочка почти ничем не отличается от второй оболочки. Поэтому свойства атомов элементов этого периода повторяют свойства атомов второго периода. В приведенной таблице показаны энергии ионизации атомов. Энергия ионизации в обоих периодах возрастает с увеличением порядкового номера (заряда ядра). Это увеличение энергии ионизации связано с увеличением силы притяжения к ядру, в результате чего понижается каждый одночастичный уровень энергии. Но для элементов третьего периода энергия ионизации меньше, чем для соответствующих элементов второго периода, что связано с увеличением главного квантового числа. Соответственно повторяются химические и оптические свойства этих элементов.
В четвертом периоде число элементов возрастает до 18. поэтому у некоторых из них нет аналогов в двух предыдущих периодах. Сначала происходит заполнение состояний  оболочки. Емкость этой подоболочки равна двум. Поэтому у элементов
оболочки. Емкость этой подоболочки равна двум. Поэтому у элементов  и
и  заполняются именно эти состояния. По своим свойствам они похожи на первые элементы второго и третьего периодов. Затем заполняются состояния
заполняются именно эти состояния. По своим свойствам они похожи на первые элементы второго и третьего периодов. Затем заполняются состояния 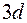 оболочки у десяти переходных элементов от
оболочки у десяти переходных элементов от  до
до  . После этого заполняется подоболочка
. После этого заполняется подоболочка 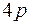 , емкостью шесть электронов. Последние шесть элементов этого периода от
, емкостью шесть электронов. Последние шесть элементов этого периода от  до
до  по своим свойствам повторяют шесть последних элементов второго и третьего периодов.
по своим свойствам повторяют шесть последних элементов второго и третьего периодов.
Пятый период таблицы так же содержит 18 элементов. И порядок заполнения электронных оболочек такой же, как в четвертом периоде. В элементах  и
и  заполняется подоболочка
заполняется подоболочка  и они обладают свойствами щелочного и щелочно-земельного металлов. Затем в десяти переходных элементах от
и они обладают свойствами щелочного и щелочно-земельного металлов. Затем в десяти переходных элементах от 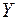 до
до  заполняется подоболочка
заполняется подоболочка  . Они аналогичны десяти элементам от
. Они аналогичны десяти элементам от  до
до  предыдущего периода. Наконец в шести элементах от
предыдущего периода. Наконец в шести элементах от 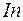 до
до  заполняется подоболочка
заполняется подоболочка 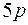 .
.
В шестом периоде таблицы содержится 32 элемента. Заполнение подоболочек идет в последовательности  ,
,  ,
,  ,
, 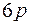 . Новая подоболочка
. Новая подоболочка  отвечает 14 элементам с близкими свойствами, которые называются лантанидами или редкоземельными элементами. Поэтому они все помещаются в одну клетку таблицы вместе с
отвечает 14 элементам с близкими свойствами, которые называются лантанидами или редкоземельными элементами. Поэтому они все помещаются в одну клетку таблицы вместе с 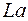 , аналогом
, аналогом  и
и 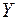 .
.
Такая же особенность наблюдается и в незавершенном седьмом периоде, где 14 элементов – актинидов, заполняющих подоболочку 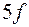 , помещаются в одну клетку с
, помещаются в одну клетку с 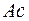 , близким по своим свойствам с
, близким по своим свойствам с 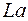 . Порядок заполнения подоболочек в седьмом периоде
. Порядок заполнения подоболочек в седьмом периоде  ,
, 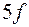 ,
,  - сходен с порядком заполнения шестого периода.
- сходен с порядком заполнения шестого периода.
В итоге периодичность в химических и оптических свойствах элементов обусловлена сходством внешних подоболочек их атомов. Так для щелочных металлов в этой подоболочке находится всего один электрон, связь которого с атомом мала. С ростом  она все более ослабевает (энергия ионизации уменьшается), так что свойство «щелочности» возрастает. В свою очередь, у галогенов в
она все более ослабевает (энергия ионизации уменьшается), так что свойство «щелочности» возрастает. В свою очередь, у галогенов в 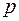 оболочке не хватает одного электрона до завершения. Поэтому все галогены стремятся приобрести лишний электрон (энергия ионизации у них больше чем у щелочных металлов), но свойство «галогенности» ослабевает с ростом
оболочке не хватает одного электрона до завершения. Поэтому все галогены стремятся приобрести лишний электрон (энергия ионизации у них больше чем у щелочных металлов), но свойство «галогенности» ослабевает с ростом  (из-за того, что уменьшается энергия ионизации).
(из-за того, что уменьшается энергия ионизации).
Аналогичным образом можно объяснить периодичность всех элементов в первых двух и последних шести столбцах таблицы Менделеева. Атомы переходных элементов в которых застраивается 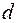 подоболочка (
подоболочка ( ), так же проявляют ряд сходных свойств. Зависимость их свойств от
), так же проявляют ряд сходных свойств. Зависимость их свойств от  слабая (энергия ионизации увеличивается медленнее, чем при застройке
слабая (энергия ионизации увеличивается медленнее, чем при застройке 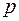 подоболочки). Полное объяснение химических свойств этих элементов, а также лантанидов и актинидов требует учета более тонких особенностей взаимодействия электронов в атомах.
подоболочки). Полное объяснение химических свойств этих элементов, а также лантанидов и актинидов требует учета более тонких особенностей взаимодействия электронов в атомах.
– Конец работы –
Эта тема принадлежит разделу:
В данной теме мы начнем изучение квантовых закономерностей явлений природы
Введение... В конце ХIX в даже у крупных ученых сложилось представление что в физике уже... Решение первой из указанных проблем привело к созданию Эйнштейном теории относительности а решение второй проблемы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Особенности периодической системы элементов
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов