Стационарные состояния. Свойства волновых функций - раздел Ядерная техника, В данной теме мы начнем изучение квантовых закономерностей явлений природы Особое Значение В Квантовой Механике Имеют Стационарные Состояния. Это Такие ...
Особое значение в квантовой механике имеют стационарные состояния. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция принципиально не наблюдаема, но с ее помощью определяются по определенным правилам значения физически наблюдаемых величин. Оказывается, что в стационарных состояниях
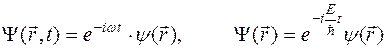 ,
,
где w - постоянная, а 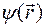 не зависит от времени.
не зависит от времени.
В стационарных состояниях плотность вероятности

от времени не зависит и является функцией только координат. Дифференцируя волновую функцию стационарных состояний по времени и подставляя результат в основное уравнение Шредингера запишем
 .
.
Это уравнение не содержит времени и называется уравнением Шредингера для стационарных состояний.
Решения этого уравнения зависят от вида потенциальной функции 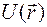 и существуют, вообще говоря, не при любых значениях величины Е. Избранные значения параметра Е, для которых имеются решения уравнения, называются собственными значениями величины Е, и соответствующие им волновые функции называются собственными функциями этого уравнения. Собственные значения Е принимаются за возможные значения энергии в стационарных состояниях.
и существуют, вообще говоря, не при любых значениях величины Е. Избранные значения параметра Е, для которых имеются решения уравнения, называются собственными значениями величины Е, и соответствующие им волновые функции называются собственными функциями этого уравнения. Собственные значения Е принимаются за возможные значения энергии в стационарных состояниях.
Собственные значения энергии могут быть дискретными (если  ) и их можно пронумеровать в порядке возрастания Е1, Е2, Е3, ..., а могут непрерывно заполнять конечный или бесконечный интервал (если Е < U(
) и их можно пронумеровать в порядке возрастания Е1, Е2, Е3, ..., а могут непрерывно заполнять конечный или бесконечный интервал (если Е < U( )). В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.
)). В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.
Квантование энергии возникает потому, что на волновые функции, являющиеся решениями уравнения Шредингера, накладываются определенные естественные ограничения. Они заключаются в том, что волновая функция  и ее первые производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции
и ее первые производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции  . Эти требования получили название стандартных условий.
. Эти требования получили название стандартных условий.
Требование однозначности волновой функции означает, что при обходе по любому замкнутому контуру (в том числе при обходе особых точек уравнения) волновая функция  должна возвращаться к своему прежнему значению. В противном случае для одной и той же точки
должна возвращаться к своему прежнему значению. В противном случае для одной и той же точки  будут иметься две или больше вероятностей
будут иметься две или больше вероятностей 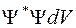 , что лишено всякого физического смысла.
, что лишено всякого физического смысла.
Требование конечности волновой функции обусловлено тем, что вероятность нахождения микрочастицы в окрестности любой точки пространства 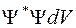 должна быть конечной.
должна быть конечной.
Требование непрерывности это естественное требование, предъявляемое к любой волновой функции (волна должна быть непрерывна в окрестности любой точки пространства).
Собственные функции  должны удовлетворять условию нормировки
должны удовлетворять условию нормировки
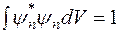 ,
,
Это означает, что вероятность обнаружения микрочастицы во всей области движения равна единице (вероятность достоверного события). Кроме того, волновые функции удовлетворяют условию ортогональности
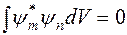 ,
,
которое означает, что интеграл от произведения различных волновых функций по всей области движения равен нулю.
Все темы данного раздела:
Равновесное тепловое излучение
1. В проблеме теплового излучения большое значение имеет понятие равновесного излучения. Чтобы представить, что это такое, рассмотрим замкнутую полость с неподвижными и непрозрачным
Формула Релея-Джинса
Чтобы определить число нормальных мод с частотами в интервале от до
Понятие вероятности. Средние значения случайных величин
1. Большинство физических величин изменяется хаотически, т.е. являются случайными величинами. Различают дискретные и непрерывные случайные величины. Дискретная величина принимает ст
Понятие о квантах. Средняя энергия осциллятора. Фотоны
1. Формирование электромагнитного поля равновесного излучения является случайным процессом, так как случайны процессы испускания света телами. Поэтому энергия любого нормального кол
Модели атома Томсона и Резерфорда
1. Согласно классическим представлениям атом мог бы испускать монохроматическую волну в том случае, когда электрон в атоме совершает гармонические колебания и следовательно, удерживается около поло
Столкновение заряженных частиц
В опытах Резерфорда применялись очень тонкие металлические фольги с толщиной порядка . Это и позволяло не учит
Формула Резерфорда и ее экспериментальная проверка
Планетарная модель атома, предложенная Резерфордом, являлась гипотезой и требовала экспериментальной проверки. Для этого Резерфорду пришлось детально проанализировать процесс рассеяния
Спектры излучения атомов.
1. С появлением первых спектральных приборов началось изучение спектров излучения и поглощения различных тел. К началу ХХ в. Было известно, что раскаленные тела излучают сплошной спектр, в котором
Постулаты Бора
Неустойчивость планетарной модели атома по Резерфорду и закономерности атомных спектров, в частности их дискре
Опыты Франка и Герца
Идея Бора о стационарных состояниях атомов получила экспериментальное подтверждение в том же 1913г. в опытах Джеймса Франка и Густава Герца.
Опыты Франка и Герца начались до появления теор
Принцип соответствия. Правило квантования
1. Н.Бор применил свои постулаты в первую очередь для анализа простейшей системы, состоящей из ядра с зарядом
Спектр излучения атома водорода
Комбинируя условие движения по окружности
и правило квантования
Орбитальный магнитный момент
При орбитальном движении электрона по круговой орбите радиусом со скоростью
Гипотеза де-Бройля. Волны де Бройля.
1. В 1923 году французский физик Луи де Бройль предположил, что корпускулярно-волновой двойственностью должны обладать не только фотоны, но и частицы вещества. Экспериментальное подтверждение этой
Дифракция микрочастиц. Опыты Дэвиссона и Джермера
2. Волновые свойства электронов были обнаружены в 1927 году в опытах Дэвиссона и Джермера, схема установки которых приведена на рис. 2.
Опыты Тартаковского и Томсона, опыты Фабриканта и Штерна
1. В последующем электронные пучки стали применять для анализа структуры кристалла. Метод этот давал более бог
Особенности поведения микрочастиц
Многочисленные эксперименты показали, что электроны, атомы, молекулы и другие частицы обладают волновыми свойствами. При этом они сохраняют свои корпускулярные свойства. Объекты, обладающие корпуск
Соотношения неопределенностей
1. Отсутствие траектории у микрочастицы указывает на то, что описывать ее состояние столь же подробно как для материальной точки нельзя.
Действительно, задание координат и импульса материа
Дифракция микрочастиц на щели
Причиной существования квантовых неопределенностей и соотношений Гейзенберга являются волновые свойства микрочастиц.
Пусть движение электрона описывается плоской волной де Бройля. Электрон
Минимальная энергия и размеры атома
Принцип неопределенности является одним из основных законов квантовой физики. Из принципа неопределенности вытекает ряд важных следствий. В частности состояние покоя для микрочастицы, движущейся в
Временное уравнение Шредингера
1. Плоская волна де Бройля
соответствует равномерному свободному движению частицы в определ
Потенциальный барьер. Решение стационарного уравнения
1. Рассмотрим рассеяние микрочастиц на преграде, испускаемых источником, удаленным на большое расстояние от нее. Силовое воздействие на микрочастицу определяется потенциальной энергией взаимодейств
Коэффициенты отражения и пропускания ступенчатого барьера
На опыте измеряются не амплитудные коэффициенты прошедшей и от-раженной волн, а коэффициенты отражения и пропускания для частиц, которые связаны с амплитудными коэффициентами вероятностными соотнош
Туннельный эффект
1. Теперь рассмотрим барьер конечной ширины (рис. 2). В этом случае в первой области будут существовать падаю
Микрочастица в одномерной прямоугольной потенциальной яме
1. Рассмотрим сначала одномерное движение микрочастицы, причем будем считать, что в области
Трехмерная потенциальная яма. Яма конечной глубины
1. В случае трехмерной потенциальной ямы решение уравнения Шредингера
,
то есть уравнение
Система двух взаимодействующих частиц
При классическом рассмотрении движение системы из двух частиц сводится к движению двух квазичастиц, одна из которых с массой
Модель гармонического осциллятора
Зависимость энергии взаимодействия двух атомов от расстояния между ними показана на рис. . При некотором расстоянии
Одномерного гармонического осциллятора
Освободившись от множителя перед второй производной, получим уравнение
, (1)
где
Момент импульса
1. Согласно классическому определению моментом импульса частицы относительно начала координат О называ
Проекции момента импульса
Выбрав за ось некоторое произвольное направление в пространстве, определим собственные функции и собственные
Координатах
1. Если силы, действующие на частицу в разных точках пространства, направлены вдоль прямых, проходящих через одну и ту же точку, называемую центром, и зависят только от расстояния до него
Спектр энергий в кулоновском поле
Используя выражение для оператора кинетической энергии радиального движения
,
уравнение (2)
Радиальные волновые функции в атоме водорода
7. Радиальные собственные функции , зависят от главного и орбитального квантовых чисел и выражаются через про
Сложение угловых моментов
1. Понятие углового момента можно распространить и на системы частиц. Для этого рассмотрим простейшую изолированную систему из двух невзаимодействующих микрочастиц: 1 и 2.
Оператором углов
Атома водорода.
В 1921 году Штерном и Герлахом был поставлен прямой опыт по обнаружению квантования магнитного момента атомов. В вакуумной камере устанавливался электромагнит со специальной формой наконечников, чт
Принцип Паули
1. Сочетание волновых и корпускулярных свойств у микрочастиц приводит к отличиям в поведении не только одиночных микрочастиц, но и в поведении коллективов частиц. Эти отличия касаются только систем
В системе однотипных микрочастиц реализуются только такие состояния, которые не меняются при перестановке местами двух любых микрочастиц.
2. Состояние системы микрочастиц описывается волновой функцией, зависящей от координат и спинов всех частиц. По-прежнему ограничимся рассмотрением системы из двух микрочастиц. Обозначим набор коорд
Особенности периодической системы элементов
Располагая химические элементы в порядке возрастания атомного веса, Менделееву пришлось отступить от этого исходного принципа и переставить места некоторых элементов, придавая большее значение пери
Спин-орбитальное взаимодействие
Основное взаимодействие электрона с ядром атома есть электростатическое взаимодействие их зарядов. Но так как электрон движется вокруг ядра, то возникает дополнительное взаимодействие, обусловленно
Энергетические уровни и спектральные серии щелочных металлов
В атомах щелочных металлов электронная оболочка содержит один наружный (валентный) электрон, сравнительно слабо связанный с ядром атома. Переходы между энергетическими уровнями валентного электрона
Результирующий механический момент атома
В многоэлектронных атомах все орбитальные и спиновые моменты электронов складываются в единый угловой момент атома. Конечно результирующий момент от порядка слагаемых не зависит, но, тем не менее,
Магнитный момент атома
С механическим моментом связан магнитный момент. Для орбитального момента
,
Сложный эффект Зеемана
Рассмотрим сначала сложный эффект Зеемана, т.е расщепление спектральных линий в слабом магнитном поле.
При наложении слабого магнитного поля появляется дополнительная энергия взаимодействи
Простой эффект Зеемана
В сильных магнитных полях воздействие на атом становится сравнимым или больше спин-орбитального взаимодействия. В этом случае уже нельзя рассматривать поведение каждой компоненты мультиплета тонкой
Гамильтониан и полная волновая функция дл атома гелия
Атом гелия является наиболее простым после атома водорода. Он содержит два электрона (Z=2). По два электрона содержат также эквивалентные ему ионы
Приближенная количественная теория атома гелия
Задача о движении двух электронов в поле ядра аналогична задаче о движении двух планет в гравитационном поле Солнца. В небесной механике разработаны достаточно точные приближенные методы расчета дв
Обменная энергия
Выпишем более подробно выражения для величин и
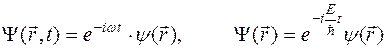 ,
,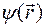 не зависит от времени.
не зависит от времени.
 .
.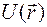 и существуют, вообще говоря, не при любых значениях величины Е. Избранные значения параметра Е, для которых имеются решения уравнения, называются собственными значениями величины Е, и соответствующие им волновые функции называются собственными функциями этого уравнения. Собственные значения Е принимаются за возможные значения энергии в стационарных состояниях.
и существуют, вообще говоря, не при любых значениях величины Е. Избранные значения параметра Е, для которых имеются решения уравнения, называются собственными значениями величины Е, и соответствующие им волновые функции называются собственными функциями этого уравнения. Собственные значения Е принимаются за возможные значения энергии в стационарных состояниях. ) и их можно пронумеровать в порядке возрастания Е1, Е2, Е3, ..., а могут непрерывно заполнять конечный или бесконечный интервал (если Е < U(
) и их можно пронумеровать в порядке возрастания Е1, Е2, Е3, ..., а могут непрерывно заполнять конечный или бесконечный интервал (если Е < U( )). В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный.
)). В первом случае говорят, что энергетический спектр дискретный, а во втором - непрерывный. и ее первые производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции
и ее первые производные должны быть конечны, однозначны и непрерывны даже в точках разрыва потенциальной функции  . Эти требования получили название стандартных условий.
. Эти требования получили название стандартных условий. должна возвращаться к своему прежнему значению. В противном случае для одной и той же точки
должна возвращаться к своему прежнему значению. В противном случае для одной и той же точки  будут иметься две или больше вероятностей
будут иметься две или больше вероятностей 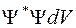 , что лишено всякого физического смысла.
, что лишено всякого физического смысла.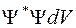 должна быть конечной.
должна быть конечной. должны удовлетворять условию нормировки
должны удовлетворять условию нормировки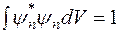 ,
,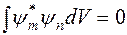 ,
,






Новости и инфо для студентов