Формула Резерфорда и ее экспериментальная проверка - раздел Ядерная техника, В данной теме мы начнем изучение квантовых закономерностей явлений природы Планетарная Модель Атома, Предложенная Резерфордом, Являлась Гипотезой И Треб...
Планетарная модель атома, предложенная Резерфордом, являлась гипотезой и требовала экспериментальной проверки. Для этого Резерфорду пришлось детально проанализировать процесс рассеяния 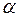 -частиц атомами тонкой металлической фольги и оценить вероятность рассеяния в телесный угол
-частиц атомами тонкой металлической фольги и оценить вероятность рассеяния в телесный угол 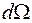 .
.
Представим, что параллельный пучок 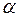 -частиц от радиоактивного источника Р площадью поперечного сечения
-частиц от радиоактивного источника Р площадью поперечного сечения 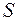 падает на тонкую металлическую фольгу Ф толщиной
падает на тонкую металлическую фольгу Ф толщиной 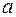 .
.
Прицельный параметр
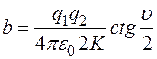 ,
,
определяющий угол рассеяния  является случайной величиной для любой частицы из потока.
является случайной величиной для любой частицы из потока.
 Для рассеяния в интервале углов
Для рассеяния в интервале углов 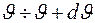 прицельный параметр должен находиться в интервале значений
прицельный параметр должен находиться в интервале значений 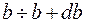 , где
, где
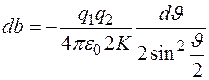 .
.
Знак минус в этом выражении отражает тот факт, что при увеличении параметра  угол рассеяния уменьшается на величину
угол рассеяния уменьшается на величину 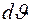 . Поэтому при оценке вероятности рассеяния мы его учитывать не будем.
. Поэтому при оценке вероятности рассеяния мы его учитывать не будем.
Величину
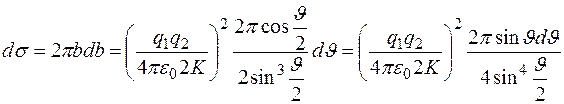
называют дифференциальным эффективным сечением рассеяния в интервале углов 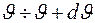 .
.
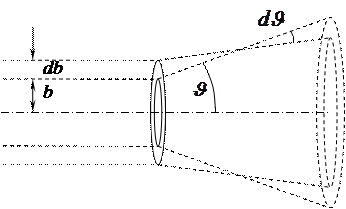
Величина 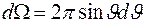 представляет собой телесный угол, заключенный между двумя коническими поверхностями с углами раствора
представляет собой телесный угол, заключенный между двумя коническими поверхностями с углами раствора 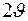 и
и 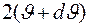 , соответственно.
, соответственно.
Толщина фольги, на которой происходило рассеяние, была порядка 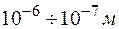 . При такой толщине ядра атомов, лежащие в различных слоях, не затеняют друг друга. Поэтому полное число центров рассеяния, попадающих в площадку
. При такой толщине ядра атомов, лежащие в различных слоях, не затеняют друг друга. Поэтому полное число центров рассеяния, попадающих в площадку 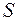 , равную площади поперечного сечения пучка
, равную площади поперечного сечения пучка 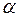 -частиц будет равно
-частиц будет равно 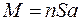 , где
, где  - концентрация атомов в фольге. Вероятность рассеяния
- концентрация атомов в фольге. Вероятность рассеяния 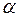 -частиц в телесный угол
-частиц в телесный угол 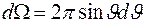 по определению представляет собой относительную долю частиц рассеянных в этот угол из всего потока частиц и равна отношению площадей
по определению представляет собой относительную долю частиц рассеянных в этот угол из всего потока частиц и равна отношению площадей  и
и 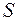
 ,
,
где 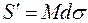 - эффективная площадь рассеяния всех ядер в телесный угол
- эффективная площадь рассеяния всех ядер в телесный угол 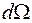 .
.
Таким образом,
 .
.
Данное соотношение называется формулой Резерфорда. В ней нужно положить заряд 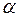 -частицы
-частицы  и заряд ядра
и заряд ядра 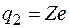 . В таком виде формула справедлива для любой площадки
. В таком виде формула справедлива для любой площадки 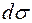 и, следовательно, для любого телесного угла
и, следовательно, для любого телесного угла 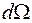 .
.
В эксперименте 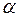 -частицы, рассеянные на угол
-частицы, рассеянные на угол  , ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр рассеивающей фольги. Весь прибор помещался в откачанный кожух с целью устранения рассеяния
, ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр рассеивающей фольги. Весь прибор помещался в откачанный кожух с целью устранения рассеяния 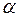 -частиц на молекулах воздуха. Так как расстояние от фольги до экрана оставалось постоянным, то телесный угол
-частиц на молекулах воздуха. Так как расстояние от фольги до экрана оставалось постоянным, то телесный угол 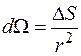 также оставался постоянным при повороте сернистого экрана на любой угол
также оставался постоянным при повороте сернистого экрана на любой угол  . Подсчитывалось число частиц, попадающих на экран за определенное время. Эксперимент подтвердил зависимость вероятности рассеяния от угла
. Подсчитывалось число частиц, попадающих на экран за определенное время. Эксперимент подтвердил зависимость вероятности рассеяния от угла  , от толщины фольги, и от энергии
, от толщины фольги, и от энергии 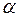 -частиц. Подтверждение формулы Резерфорда на опыте можно рассматривать как косвенное доказательство справедливости закона Кулона до расстояний
-частиц. Подтверждение формулы Резерфорда на опыте можно рассматривать как косвенное доказательство справедливости закона Кулона до расстояний 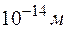 .
.
Эксперименты по рассеянию легких ядер на тяжелых в ускорителях показали, что при расстояниях между сталкивающимися ядрами меньше 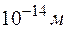 наблюдаются отклонения от закона Кулона. На таких расстояниях проявляют свое действие ядерные силы притяжения, перекрывающие кулоновские силы отталкивания.
наблюдаются отклонения от закона Кулона. На таких расстояниях проявляют свое действие ядерные силы притяжения, перекрывающие кулоновские силы отталкивания.
Все темы данного раздела:
Равновесное тепловое излучение
1. В проблеме теплового излучения большое значение имеет понятие равновесного излучения. Чтобы представить, что это такое, рассмотрим замкнутую полость с неподвижными и непрозрачным
Формула Релея-Джинса
Чтобы определить число нормальных мод с частотами в интервале от до
Понятие вероятности. Средние значения случайных величин
1. Большинство физических величин изменяется хаотически, т.е. являются случайными величинами. Различают дискретные и непрерывные случайные величины. Дискретная величина принимает ст
Понятие о квантах. Средняя энергия осциллятора. Фотоны
1. Формирование электромагнитного поля равновесного излучения является случайным процессом, так как случайны процессы испускания света телами. Поэтому энергия любого нормального кол
Модели атома Томсона и Резерфорда
1. Согласно классическим представлениям атом мог бы испускать монохроматическую волну в том случае, когда электрон в атоме совершает гармонические колебания и следовательно, удерживается около поло
Столкновение заряженных частиц
В опытах Резерфорда применялись очень тонкие металлические фольги с толщиной порядка . Это и позволяло не учит
Спектры излучения атомов.
1. С появлением первых спектральных приборов началось изучение спектров излучения и поглощения различных тел. К началу ХХ в. Было известно, что раскаленные тела излучают сплошной спектр, в котором
Постулаты Бора
Неустойчивость планетарной модели атома по Резерфорду и закономерности атомных спектров, в частности их дискре
Опыты Франка и Герца
Идея Бора о стационарных состояниях атомов получила экспериментальное подтверждение в том же 1913г. в опытах Джеймса Франка и Густава Герца.
Опыты Франка и Герца начались до появления теор
Принцип соответствия. Правило квантования
1. Н.Бор применил свои постулаты в первую очередь для анализа простейшей системы, состоящей из ядра с зарядом
Спектр излучения атома водорода
Комбинируя условие движения по окружности
и правило квантования
Орбитальный магнитный момент
При орбитальном движении электрона по круговой орбите радиусом со скоростью
Гипотеза де-Бройля. Волны де Бройля.
1. В 1923 году французский физик Луи де Бройль предположил, что корпускулярно-волновой двойственностью должны обладать не только фотоны, но и частицы вещества. Экспериментальное подтверждение этой
Дифракция микрочастиц. Опыты Дэвиссона и Джермера
2. Волновые свойства электронов были обнаружены в 1927 году в опытах Дэвиссона и Джермера, схема установки которых приведена на рис. 2.
Опыты Тартаковского и Томсона, опыты Фабриканта и Штерна
1. В последующем электронные пучки стали применять для анализа структуры кристалла. Метод этот давал более бог
Особенности поведения микрочастиц
Многочисленные эксперименты показали, что электроны, атомы, молекулы и другие частицы обладают волновыми свойствами. При этом они сохраняют свои корпускулярные свойства. Объекты, обладающие корпуск
Соотношения неопределенностей
1. Отсутствие траектории у микрочастицы указывает на то, что описывать ее состояние столь же подробно как для материальной точки нельзя.
Действительно, задание координат и импульса материа
Дифракция микрочастиц на щели
Причиной существования квантовых неопределенностей и соотношений Гейзенберга являются волновые свойства микрочастиц.
Пусть движение электрона описывается плоской волной де Бройля. Электрон
Минимальная энергия и размеры атома
Принцип неопределенности является одним из основных законов квантовой физики. Из принципа неопределенности вытекает ряд важных следствий. В частности состояние покоя для микрочастицы, движущейся в
Временное уравнение Шредингера
1. Плоская волна де Бройля
соответствует равномерному свободному движению частицы в определ
Стационарные состояния. Свойства волновых функций
Особое значение в квантовой механике имеют стационарные состояния. Это такие состояния, в которых все наблюдаемые физические параметры не меняются с течением времени. Сама волновая функция принципи
Потенциальный барьер. Решение стационарного уравнения
1. Рассмотрим рассеяние микрочастиц на преграде, испускаемых источником, удаленным на большое расстояние от нее. Силовое воздействие на микрочастицу определяется потенциальной энергией взаимодейств
Коэффициенты отражения и пропускания ступенчатого барьера
На опыте измеряются не амплитудные коэффициенты прошедшей и от-раженной волн, а коэффициенты отражения и пропускания для частиц, которые связаны с амплитудными коэффициентами вероятностными соотнош
Туннельный эффект
1. Теперь рассмотрим барьер конечной ширины (рис. 2). В этом случае в первой области будут существовать падаю
Микрочастица в одномерной прямоугольной потенциальной яме
1. Рассмотрим сначала одномерное движение микрочастицы, причем будем считать, что в области
Трехмерная потенциальная яма. Яма конечной глубины
1. В случае трехмерной потенциальной ямы решение уравнения Шредингера
,
то есть уравнение
Система двух взаимодействующих частиц
При классическом рассмотрении движение системы из двух частиц сводится к движению двух квазичастиц, одна из которых с массой
Модель гармонического осциллятора
Зависимость энергии взаимодействия двух атомов от расстояния между ними показана на рис. . При некотором расстоянии
Одномерного гармонического осциллятора
Освободившись от множителя перед второй производной, получим уравнение
, (1)
где
Момент импульса
1. Согласно классическому определению моментом импульса частицы относительно начала координат О называ
Проекции момента импульса
Выбрав за ось некоторое произвольное направление в пространстве, определим собственные функции и собственные
Координатах
1. Если силы, действующие на частицу в разных точках пространства, направлены вдоль прямых, проходящих через одну и ту же точку, называемую центром, и зависят только от расстояния до него
Спектр энергий в кулоновском поле
Используя выражение для оператора кинетической энергии радиального движения
,
уравнение (2)
Радиальные волновые функции в атоме водорода
7. Радиальные собственные функции , зависят от главного и орбитального квантовых чисел и выражаются через про
Сложение угловых моментов
1. Понятие углового момента можно распространить и на системы частиц. Для этого рассмотрим простейшую изолированную систему из двух невзаимодействующих микрочастиц: 1 и 2.
Оператором углов
Атома водорода.
В 1921 году Штерном и Герлахом был поставлен прямой опыт по обнаружению квантования магнитного момента атомов. В вакуумной камере устанавливался электромагнит со специальной формой наконечников, чт
Принцип Паули
1. Сочетание волновых и корпускулярных свойств у микрочастиц приводит к отличиям в поведении не только одиночных микрочастиц, но и в поведении коллективов частиц. Эти отличия касаются только систем
В системе однотипных микрочастиц реализуются только такие состояния, которые не меняются при перестановке местами двух любых микрочастиц.
2. Состояние системы микрочастиц описывается волновой функцией, зависящей от координат и спинов всех частиц. По-прежнему ограничимся рассмотрением системы из двух микрочастиц. Обозначим набор коорд
Особенности периодической системы элементов
Располагая химические элементы в порядке возрастания атомного веса, Менделееву пришлось отступить от этого исходного принципа и переставить места некоторых элементов, придавая большее значение пери
Спин-орбитальное взаимодействие
Основное взаимодействие электрона с ядром атома есть электростатическое взаимодействие их зарядов. Но так как электрон движется вокруг ядра, то возникает дополнительное взаимодействие, обусловленно
Энергетические уровни и спектральные серии щелочных металлов
В атомах щелочных металлов электронная оболочка содержит один наружный (валентный) электрон, сравнительно слабо связанный с ядром атома. Переходы между энергетическими уровнями валентного электрона
Результирующий механический момент атома
В многоэлектронных атомах все орбитальные и спиновые моменты электронов складываются в единый угловой момент атома. Конечно результирующий момент от порядка слагаемых не зависит, но, тем не менее,
Магнитный момент атома
С механическим моментом связан магнитный момент. Для орбитального момента
,
Сложный эффект Зеемана
Рассмотрим сначала сложный эффект Зеемана, т.е расщепление спектральных линий в слабом магнитном поле.
При наложении слабого магнитного поля появляется дополнительная энергия взаимодействи
Простой эффект Зеемана
В сильных магнитных полях воздействие на атом становится сравнимым или больше спин-орбитального взаимодействия. В этом случае уже нельзя рассматривать поведение каждой компоненты мультиплета тонкой
Гамильтониан и полная волновая функция дл атома гелия
Атом гелия является наиболее простым после атома водорода. Он содержит два электрона (Z=2). По два электрона содержат также эквивалентные ему ионы
Приближенная количественная теория атома гелия
Задача о движении двух электронов в поле ядра аналогична задаче о движении двух планет в гравитационном поле Солнца. В небесной механике разработаны достаточно точные приближенные методы расчета дв
Обменная энергия
Выпишем более подробно выражения для величин и
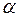 -частиц атомами тонкой металлической фольги и оценить вероятность рассеяния в телесный угол
-частиц атомами тонкой металлической фольги и оценить вероятность рассеяния в телесный угол 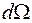 .
.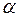 -частиц от радиоактивного источника Р площадью поперечного сечения
-частиц от радиоактивного источника Р площадью поперечного сечения 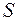 падает на тонкую металлическую фольгу Ф толщиной
падает на тонкую металлическую фольгу Ф толщиной 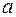 .
.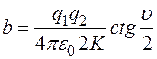 ,
, является случайной величиной для любой частицы из потока.
является случайной величиной для любой частицы из потока. Для рассеяния в интервале углов
Для рассеяния в интервале углов 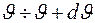 прицельный параметр должен находиться в интервале значений
прицельный параметр должен находиться в интервале значений 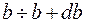 , где
, где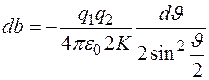 .
. угол рассеяния уменьшается на величину
угол рассеяния уменьшается на величину 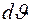 . Поэтому при оценке вероятности рассеяния мы его учитывать не будем.
. Поэтому при оценке вероятности рассеяния мы его учитывать не будем.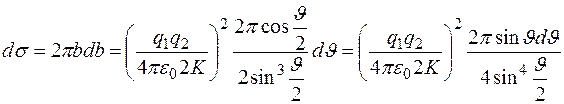
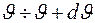 .
.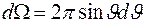 представляет собой телесный угол, заключенный между двумя коническими поверхностями с углами раствора
представляет собой телесный угол, заключенный между двумя коническими поверхностями с углами раствора 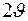 и
и 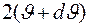 , соответственно.
, соответственно.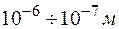 . При такой толщине ядра атомов, лежащие в различных слоях, не затеняют друг друга. Поэтому полное число центров рассеяния, попадающих в площадку
. При такой толщине ядра атомов, лежащие в различных слоях, не затеняют друг друга. Поэтому полное число центров рассеяния, попадающих в площадку 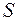 , равную площади поперечного сечения пучка
, равную площади поперечного сечения пучка 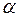 -частиц будет равно
-частиц будет равно 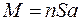 , где
, где  - концентрация атомов в фольге. Вероятность рассеяния
- концентрация атомов в фольге. Вероятность рассеяния 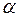 -частиц в телесный угол
-частиц в телесный угол 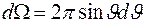 по определению представляет собой относительную долю частиц рассеянных в этот угол из всего потока частиц и равна отношению площадей
по определению представляет собой относительную долю частиц рассеянных в этот угол из всего потока частиц и равна отношению площадей  и
и 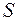
 ,
,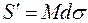 - эффективная площадь рассеяния всех ядер в телесный угол
- эффективная площадь рассеяния всех ядер в телесный угол 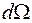 .
. .
.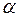 -частицы
-частицы  и заряд ядра
и заряд ядра 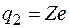 . В таком виде формула справедлива для любой площадки
. В таком виде формула справедлива для любой площадки 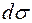 и, следовательно, для любого телесного угла
и, следовательно, для любого телесного угла 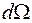 .
.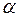 -частицы, рассеянные на угол
-частицы, рассеянные на угол  , ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр рассеивающей фольги. Весь прибор помещался в откачанный кожух с целью устранения рассеяния
, ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр рассеивающей фольги. Весь прибор помещался в откачанный кожух с целью устранения рассеяния 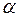 -частиц на молекулах воздуха. Так как расстояние от фольги до экрана оставалось постоянным, то телесный угол
-частиц на молекулах воздуха. Так как расстояние от фольги до экрана оставалось постоянным, то телесный угол 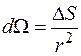 также оставался постоянным при повороте сернистого экрана на любой угол
также оставался постоянным при повороте сернистого экрана на любой угол  . Подсчитывалось число частиц, попадающих на экран за определенное время. Эксперимент подтвердил зависимость вероятности рассеяния от угла
. Подсчитывалось число частиц, попадающих на экран за определенное время. Эксперимент подтвердил зависимость вероятности рассеяния от угла  , от толщины фольги, и от энергии
, от толщины фольги, и от энергии 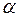 -частиц. Подтверждение формулы Резерфорда на опыте можно рассматривать как косвенное доказательство справедливости закона Кулона до расстояний
-частиц. Подтверждение формулы Резерфорда на опыте можно рассматривать как косвенное доказательство справедливости закона Кулона до расстояний 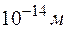 .
.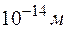 наблюдаются отклонения от закона Кулона. На таких расстояниях проявляют свое действие ядерные силы притяжения, перекрывающие кулоновские силы отталкивания.
наблюдаются отклонения от закона Кулона. На таких расстояниях проявляют свое действие ядерные силы притяжения, перекрывающие кулоновские силы отталкивания.






Новости и инфо для студентов