Линейная алгебра

ВВЕДЕНИЕ

 

В настоящее время линейная алгебра широко используется во многих разделах теоретической и прикладной математики. Математическая структура линейной алгебры исключительно проста и основывается на небольшом числе удобных в обращении первичных понятий, операций и аксиом.

Линейная алгебра, как и любая другая математическая теория, строится по аксиоматическому принципу. Согласно этому подходу вводится ряд объектов, называемых первичными, которые не определяются строго, а только поясняются на примерах. Далее с этими объектами связываются некоторые операции и формулируются аксиомы. На основе первичных понятий и аксиом по правилам математической логики развивается дальнейшая теория: доказываются теоремы и леммы, выводятся следствия, формулируются необходимые определения.

ЛИНЕЙНОЕ ПРОСТРАНСТВО

1. Имеется операция сложения векторов, по которой каждой упорядоченной паре векторов ставится в соответствие третий вектор, что обозначается как . … 2. Имеется операция умножения числа на вектор, по которой каждой упорядоченной… 3. Для любых векторов из и чисел указанные операции удовлетворяют следующим восьми аксиомам:

Множество числовых функций.

Множество всех полиномов степени не выше .

Например, и полиномы второй степени, а их сумма является полиномом первой степени. Из аксиом, определяющих линейное пространство, можно в качестве логических… Определение. Вектор , удовлетворяющий уравнению для любых из , называют разностью векторов и, и обозначают . Операцию,…

Теорема (о существовании и единственности разности элементов).

Доказательство.Покажем, что такой вектор существует. Возьмем и убедимся, что этот элемент удовлетворяет уравнению . Действительно, . Докажем, что этот вектор единственный. Возьмем другой вектор из , удовлетворяющий нашему уравнению , и выполним…

Теорема (об условиях равенства нулю произведения числа на вектор).

Доказательство.Пусть число равно нулю или вектор является нулевым. Покажем, что . Пусть вначале . Справедливо . В силу единственности нулевого… Обратно, пусть . Покажем, что или . Доказательство проведем методом от… С другой стороны, по нашему предположению и аксиомам имеем . Полученное противоречие доказывает вторую часть…

МАТРИЦЫ И ОПЕРАЦИИ НАД НИМИ

 

Матрицы и определители матриц широко используются при решении систем линейных уравнений, линейном программировании, исследовании систем дифференциальных уравнений. Аппарат теории матриц применяется в вычислительной математике, физике, моделировании практических задач в технике, экономике и бизнесе.

Матрицей называется прямоугольная таблица, составленная из 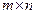элементов 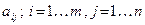некоторого множества. Матрицы обычно обозначают заглавными буквами латинского алфавита в виде 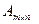, если важно знать ее размеры, или буквами 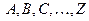. Записывается матрица в следующем виде .

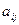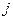Элементы матрицы нумеруются двумя индексами. Первый индекс обозначает номер строки, а второй – номер столбца, на пересечении которых находится этот элемент в матрице. Матрица называется числовой, если ее элементы вещественные или комплексные числа; функциональной, если ее элементы – функции; блочной, если ее элементы – другие матрицы. Если число строк матрицы равно числу ее столбцов, то матрицу называют квадратной. Все элементы квадратной матрицы, которые имеют одинаковые первые и вторые индексы, образуют главную диагональ матрицы. Если матрица имеет только одну строку, то ее называют матрицей – строкой или вектор – строкой. Такая матрица совпадает с арифметическим вектором, и ее элементы отделяют друг от друга запятыми. Если матрица имеет только один столбец, то ее называют матрицей – столбцом или вектор – столбцом. По соглашению, арифметические векторы записывают в виде вектор – столбцов.Например, матрица 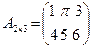- прямоугольная числовая матрица размером две строки на три столбца, матрица 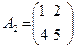- квадратная числовая матрица размером две строки на два столбца, матрица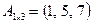- это матрица – строка, а матрица 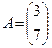- матрица – столбец.

Некоторые матрицы имеют специальные обозначения и названия.

Произвольная матрица называется нулевой, если все ее элементы равны нулю. Например, матрица 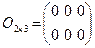– нулевая размером два на три.

Квадратная матрица называется единичной, если все ее элементы на главной диагонали равны единице, а все остальные элементы равны нулю. Так, матрица 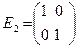- единичная и имеет размеры два на два.

Квадратная матрица называется диагональной, если ее элементы, стоящие выше и ниже главной диагонали равны нулю. Например, матрица 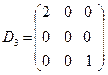- диагональная.

Если в матрице 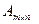размером 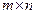заменить строки на столбцы с тем же номером, то получится новая матрица 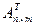размером 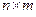, которую называют транспонированной к исходной матрице 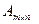. Таким образом, по определению для всех элементов транспонированной матрицы выполняются соотношения: 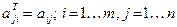. Например, транспонированной по отношению к матрице 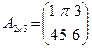размером две строки на три столбца будет матрица 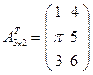размером три строки на два столбца. Если дважды транспонировать матрицу, то в результате получится исходная матрица.

Матрицы и 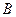называют равными, если они имеют одинаковые размеры и все их соответствующие элементы равны, т.е. 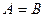, если .

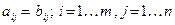Например, числовая матрица 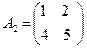равна квадратной, функциональной матрице 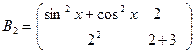, но они записаны в различных формах.

Квадратная матрица 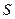называется симметричной, если она совпадает с транспонированной матрицей, т.е. 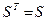. Например, матрица 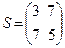- симметричная, и видно, что она симметрична относительно главной диагонали. Отметим также, что диагональная и единичная матрицы являются симметричными, так как они совпадают со своими транспонированными матрицами, что проверяется непосредственно.

Для матриц введены две основные операции: сложение матриц и умножение матрицы на число (вещественное или комплексное).

Суммой 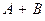двух матриц одинакового размера называется матрица 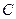того же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц, то есть .

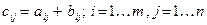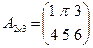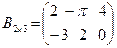Так, если и , то .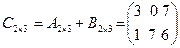

Для операции сложения матриц выполняются свойства коммутативности 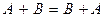и ассоциативности 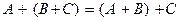, которые следуют из соответствующих свойств чисел. Если к любой матрице прибавить слева или справа нулевую матрицу, то исходная матрица не изменится; таким образом, выполняются равенства 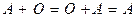. Для любой матрицы существует единственная противоположная матрица 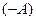, такая что 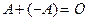, что также следует из аксиоматических свойств чисел. Разность двух матриц одинаковых размеров определяется как обычно по правилу 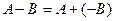, то есть соответствующие элементы первой и второй матриц вычитаются. Так, если

 

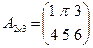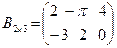и , то .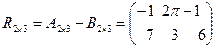

Произведением 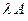матрицы на число 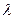(вещественное или комплексное) называется матрица 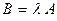, полученная из исходной матрицы умножением всех ее элементов на число 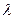, то есть .

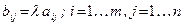Например, пусть 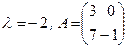. Тогда .

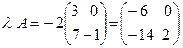Для основных матричных операций выполняются, дополнительно к вышеуказанным четырем свойствам, следующие четыре свойства:

- при умножении на число 1 матрица не изменяется ,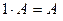

- ассоциативность умножения на числа ,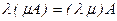

- две дистрибутивности и 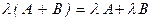. Все свойства матриц следуют из соответствующих свойств чисел.

Таким образом, для матриц относительно основных операций сложения и умножения на число выполняются все восемь аксиом линейного пространства. Это позволяет считать матрицы элементами некоторого конкретного линейного пространства и обращаться с ними как с векторами. Отметим, что арифметические векторы по их определению совпадают с матрицами – строками или матрицами – столбцами. Следовательно, арифметические векторы также удовлетворяют всем восьми свойствам абстрактного линейного пространства и могут, как и матрицы, называться векторами.

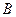Операция умножения первой матрицы на вторую матрицу не является основной. Эта операция определяется только в том случае, когда число столбцов первой равно числу строк второй (длина строк первой матрицы равна высоте столбцов второй матрицы).

Произведением 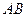матрицы размера 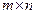на матрицу 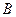размера 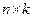называется матрица 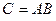размера 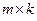, все элементы которой находятся по формулам

.

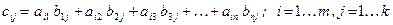Таким образом, для нахождения элементов 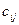последовательно выбираются строки и столбцы, причем при каждом выборе элементы строки умножаются на соответствующие элементы столбца и все такие парные произведения складываются. Пусть, например, первая матрица 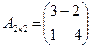имеет размер две строки на два столбца, вторая матрица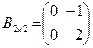- такой же размер. Тогда матрица 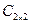, равная их произведению 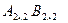, находится по определяющим формулам в виде 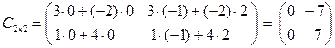и также имеет размер две строки на два столбца. Так как матрицы 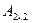и 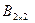квадратные, то их можно перемножить в обратном порядке, то есть найти

 

.

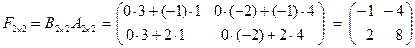Мы получили в нашем случае, что 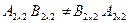. Этот контрпример доказывает, что в общем случае умножение матриц не подчиняется закону коммутативности. Существуют матрицы, для которых свойство коммутативности выполняется. Такие матрицы называют коммутирующими, и они обязательно должны быть квадратными.

Покажем, например, что матрицы 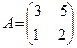и 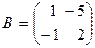коммутирующие. Действительно

,

,

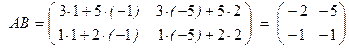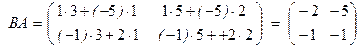что и доказывает наше утверждение.

Если матрица 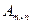не является квадратной, то есть 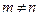, то ее нельзя умножить саму на себя, так как число столбцов первой матрицы не будет равно числу строк второй матрицы. Однако если ее транспонировать, то определено как произведение 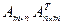размера 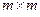, так и произведение 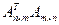размера 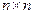. Рассмотрим для примера матрицу – строку вида 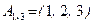. Транспонированная к ней матрица будет матрицей – столбцом вида 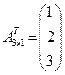. Произведение 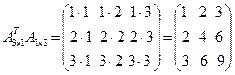будет иметь размер три на три, а произведение 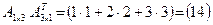будет иметь размер одна строка на один столбец. Сформируем далее матрицу

.

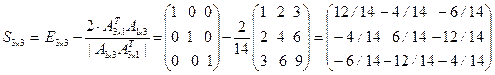В этой формуле символом 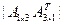обозначен определитель матрицы 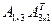, состоящей из одного элемента. Как показывается ниже, определитель такой матрицы равен значению этого единственного элемента. Полученная матрица симметричная и при умножении на себя дает единичную матрицу.

Основные свойства, связанные с умножением матриц, доказываются в общем виде на основе соответствующих свойств чисел путем непосредственного сопоставления матриц слева и справа от знака равенства:

1) ,

2) ,

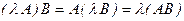3) ,

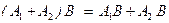4) ,

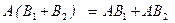5) ,

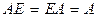6) .

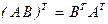ОПРЕДЕЛИТЕЛИ МАТРИЦ И ИХ СВОЙСТВА

Определители вводятся только для квадратных матриц как некоторое правило, формирующее значение определителя по элементам матрицы. Если элементы… Определитель матрицы положим равным элементу . Так, например, . Определителем порядка назовем число, которое будем находить по правилу разложения по первой строке матрицы размера : …

Теорема (о разложении определителя по любой строке или столбцу).

Например, формула разложения определителя по той строке в соответствии с основной теоремой имеет вид: Этой теоремой широко пользуются при вычислении определителей, стараясь выбирать те строки или столбцы, которые…

Теорема (теорема аннулирования).

Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам любой другой строки (столбца) равна нулю.

Доказательство.

  . Вид этой формулы не зависит от того, какие конкретно значения имеют элементы первой строки. Поместим в первую строку…

Теорема (об определителе произведения двух матриц).

Теорема приводится без доказательства. Следующий пример   , , ,

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Коэффициенты при неизвестных объединяют в так называемую матрицу системы ,… Обычно, для более краткой записи нижние индексы матриц опускают и систему уравнений в матричной форме представляют в…

Теорема (о существовании и единственности обратной матрицы).

Матрицаназывается присоединенной по отношению к матрице , и ее столбцы состоят из алгебраических дополнений к элементам, расположенным в…

Доказательство.

Таким образом: . Аналогично доказывается, что произведение , что означает существование… Покажем, что эта матрица единственная. Предположим, что имеется хотя бы одна матрица , также удовлетворяющая условиям…

Теорема Крамера.

где матрицы получены из матрицы заменой -тых столбцов на столбец правых частей системы.

Доказательство.

Таким образом, доказано, что матричным способом вектор – столбец решений находится в единственном виде по формуле . Если далее формулу представить в покомпонентной записи, то для компонент… ,,

Базис множества векторов и всего линейного пространства.

Если множество совпадает со всем пространством , то базис является базисом всего линейного пространства. Числа называются координатами вектора в базисе , а выражение - разложением…

Теорема (о единственности разложения по данному базису).

Доказательство.Предположим, что для вектора наряду с разложением имеется другое разложение . Вычитая одно разложение из другого, получим равенство… Поскольку базисные векторы линейно независимы, то из полученного равенства… Следствие.Любые два вектора равны тогда и только тогда, когда равны их координаты в каком – либо базисе.

Теорема (о линейных свойствах координат векторов).

Доказательство.Пусть любые два вектора имеют в базисе разложения , . Из аксиом линейного пространства следует, что сумма векторов и произведение… Отсюда и теоремы о единственности разложения векторов по данному базису…

Теорема о базисном миноре.

Базисные строки (столбцы) линейно независимы и образуют базис в системе всех строк (столбцов) произвольной матрицы размера .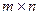

Доказательство.

Линейную независимость базисных строк будем доказывать методом от обратного. Пусть некоторые базисные строки линейно зависимы. Тогда одна из этих строк… Докажем теперь, что любая строка произвольной матрицы размера является линейной комбинацией базисных строк. Для…

Доказательство.

Покажем, что условие линейной зависимости столбцов квадратной матрицы является необходимымдля равенства нулю определителя матрицы. Если определитель… Если размеры матрицы большие, то ранг матрицы вычисляют, пользуясь методом… Элементарными преобразованиями матрицы называют следующие:

Теорема (о приведении к ступенчатой матрице).

Теорема доказывается конструктивно путем перебора конечного числа возможных матриц с нулевыми элементами. Пример.Приведем к ступенчатому виду следующую матрицу: . На первом шаге выполним следующие элементарные преобразования над матрицей : к элементам второй строки прибавим…

Теорема (о ранге ступенчатой матрицы).

Доказательство.Ненулевые, ступенчатые строки линейно независимы, что можно показать, составив линейную комбинацию этих строк и приравняв ее нулевой…

Теорема (об инвариантности ранга при элементарных преобразованиях).

Ранг матрицы не изменяется при ее элементарных преобразованиях.

Доказательство.При любых элементарных преобразованиях отличный от нуля определитель остается таковым. Поэтому любой найденный базисный минор останется базисным. Миноры более высокого порядка равны нулю и останутся таковыми при любых элементарных преобразованиях. Таким образом, теорема доказана.

На основе трех, приведенных выше теорем, формулируется метод элементарных преобразований:сначала исходная матрица приводится к ступенчатому виду, затем ранг исходной матрицы полагается равным числу ненулевых строк ступенчатой матрицы.

В рассмотренном выше примере матрица была приведена элементарными преобразованиями к ступенчатой матрице, имеющей три ненулевые строки. Это означает, что ранг исходной матрицы равен трем.

Исследуя систему уравнений общего вида, необходимо либо доказать, что она не имеет решений, либо, если она совместна, найти все возможные решения и представить их в компактной и наглядной форме. Для этого систему уравнений с помощью элементарных преобразований приводят к более простому виду, позволяющему непосредственно увидеть решения или показать несовместность системы. При этом центральным понятием является равносильность двух систем. Две системы уравнений с одними теми же неизвестными называются равносильными,если они имеют одно и то же множество решений.

Например, системы 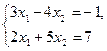и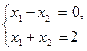являются равносильными, так как каждая из них имеет одно и то же единственное решение .

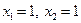Системы 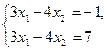и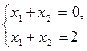также являются равносильными, поскольку каждая из них не имеет решений (множество решений пусто).

Элементарными преобразованиями системы линейных алгебраических уравнений называют следующие преобразования:

1) перестановка местами любых двух уравнений;

2) умножение любого уравнения системы на одно и то же число, отличное от нуля;

3) сложение любых двух уравнений.

Теорема (о равносильных переходах).

Доказательство теоремы следует непосредственно из определения элементарных преобразований системы линейных уравнений общего вида. Как видно из приведенных определений, элементарным преобразованиям системы… расширенной матрицы системы, которая получается из матрицы коэффициентов системы добавлением - го столбца, состоящего…

Сущность метода Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к виду, из которого все ее решения усматриваются непосредственно.

На первом этапе (прямой ход метода Гаусса) расширенная матрица 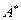приводится к ступенчатой матрице 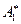, у которой все ненулевые строки имеют первый элемент, равный единице. Решение полученной системы уравнений с расширенной ступенчатой матрицей 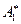называется обратным ходом метода Гаусса. Обратный ход может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего, так и в форме последующего преобразования матрицы 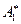к ступенчатой матрице 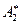, у которой все ненулевые строки содержат только одну единицу и позволяют в явном виде представить решение системы.

Пример.Решим методом Гаусса следующую систему: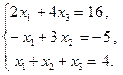

Выполняя прямой ход метода Гаусса, приведем расширенную матрицу этой системы 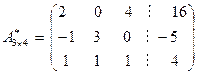к ступенчатой матрице, у которой все ненулевые строки имеют первый ненулевой элемент, равный единице. На первом этапе выполним следующие элементарные преобразования исходной расширенной матрицы: разделим первую строку на число два; сложим вторую строку с первой и результат запишем во вторую строку; из третьей строки вычтем преобразованную первую строку и результат запишем в третью строку:

.

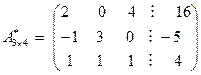
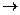
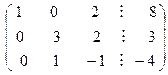Мы получили в результате, что первая строка ненулевая, имеет первым ненулевым элементом число один, а все элементы в первой колонке под числом один равны нулю. Для того чтобы, вторая строка начиналась с единицы, переставим вторую и третью строки местами:

.

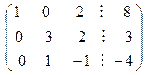
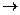
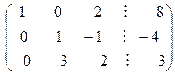Для того чтобы под единицей во втором столбце стоял нуль, из третьей строки полученной матрицы вычтем вторую строку, умноженную на три, и запишем в третью строку:

.

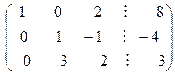
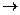
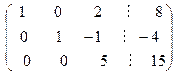Наконец, чтобы третья строка имела первым ненулевым элементом число один, поделим третью строку на число пять:

=.

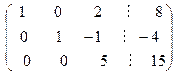
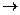
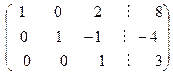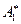На этом завершается прямой ход метода Гаусса, а преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице, равносильна исходной системе уравнений и имеет следующий вид:

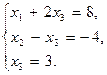
Отметим, что, выполняя прямой ход метода Гаусса, мы получаем возможность эффективного вычисления ранга матрицы и определителя матрицы. Если нас интересует ранг матрицы, то после преобразования ее к ступенчатой форме, достаточно подсчитать число ненулевых строк: это и будет ранг матрицы.

Если нас интересует определитель матрицы, то эта матрица, естественно, должна быть квадратной. После преобразования ее методом Гаусса к ступенчатой форме она примет вид верхней треугольной матрицы, то есть матрицы, у которой все элементы ниже главной диагонали равны нулю. Определитель любой верхней треугольной матрицы равен произведению всех элементов, стоящих на главной диагонали. Если на главной диагонали имеется хотя бы один нулевой элемент, то определитель треугольной матрицы равен нулю и, соответственно, определитель исходной матрицы равен нулю. Если же на главной диагонали в результате преобразований прямого хода метода Гаусса окажутся только единицы, то надо в процессе преобразований следить за перестановками строк, которые изменяют знак определителя на обратный, и за умножениями или делениями строк матрицы на числа, которые пропорционально изменяют величину определителя. Определитель исходной матрицы находится как произведение всех чисел, на которые делились строки. Знак этого произведения остается прежним, если было проведено четное число перестановок строк, и изменяется на противоположный, если число перестановок строк было нечетным.

В нашем примере, выполнив прямой ход метода Гаусса, мы одновременно нашли ранг матрицы коэффициентов системы (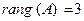, так как число ненулевых строк преобразованной матрицы равно трем), а также ранг расширенной матрицы (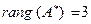, так как число ненулевых строк преобразованной матрицы 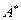равно трем).

Для вычисления определителя исходной матрицы коэффициентов необходимо обратить внимание на три обстоятельства: вид верхней треугольной матрицы, в которую преобразовалась исходная матрица; на какие числа делились или умножались строки; какое количество (четное или нечетное) перестановок было выполнено в процессе преобразований. Так как на главной диагонали стоят только единицы, то определитель не равен нулю. Далее в процессе преобразований было использовано деление на число 2 первой строки и деление на число 5 третьей строки. Их надо перемножить 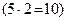и подсчитать число перестановок строк местами: была выполнена одна перестановка. Таким образом, определитель матрицы коэффициентов равен: .

Выполним обратный ход метода Гаусса сначала первым способом, то есть последовательно определим неизвестные, начиная с последнего уравнения:

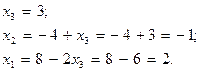
Выполним обратный ход метода Гаусса вторым способом. Продолжим элементарные преобразования матрицы и приведем ее к ступенчатой матрице , у которой все ненулевые строки содержат только одну единицу. Это позволит в явном виде представить решение системы. Сложим вторую строку с третьей строкой и результат запишем во вторую строку:

= .

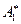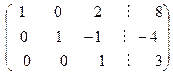
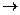
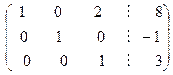Далее, чтобы заменить число два первой строки на число нуль, умножим третью строку на число (-2), сложим с первой строкой и результат запишем в первую строку:

.

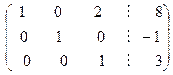
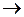
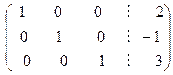На этом заканчивается обратный ход метода Гаусса. Преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице типа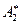, равносильна исходной системе уравнений и имеет следующий вид

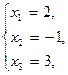
который представляет собой запись решения системы в явной форме.

Для исследования решения систем линейных уравнений с произвольным числом уравнений и неизвестных полезна следующая теорема.

Теорема Кронекера – Капелли.

Для того чтобы произвольная система линейных уравнений 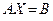была совместной, необходимо и достаточно, чтобы ранг матрицы коэффициентов был равен рангу расширенной матрицы, то есть .

Доказательство.

  . С точностью до обозначения неизвестных, полученной ступенчатой матрице соответствует ступенчатая система уравнений,…

Исследование и решение однородных систем уравнений.

Если дополнительно ранг матрицы коэффициентов равен числу неизвестных системы , то, учитывая выполнение всех условий следствия 1 из теоремы… Если система линейных уравнений однородна и , то ее множество решений… Прежде чем построить эти решения приведем необходимые определения и теоремы, справедливые для любых линейных…

Доказательство.

Тогда по определению линейной зависимости векторов справедливо равенство , причем среди коэффициентов линейной комбинации в правой части равенства… Достаточность. Пусть векторы образуют базис некоторого линейного пространства.… Разложим эти векторы по исходному базису в следующем виде:

Пример.

Рассмотрим в пространстве арифметических векторов с компонентами следующую систему из векторов: 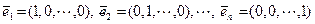. Эта система векторов является линейно независимой системой, так как непосредственно видно, что линейная комбинация равна нулевому вектору только в том случае, когда все коэффициенты 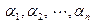равны нулю. Покажем, что любой арифметический вектор с компонентами 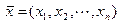может быть разложен по векторам .

Действительно, справедливы следующие равенства:

.

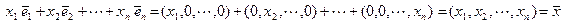Таким образом, система векторов 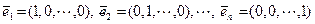образует базис в пространстве всех арифметических векторов с компонентами, который принято называть каноническим базисом, а в соответствии с доказанной выше теоремой рассматриваемое в примере линейное пространство имеет размерность .

Определение. Если некоторое непустое подмножество линейного пространства замкнуто относительно основных операций сложения и умножения на число исходного пространства, то оно называется подпространством.

Иначе говоря, если два любых вектора 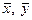принадлежат подпространству, то их сумма и произведение на любое число 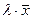также входят в подпространство.

Для всякого линейного пространства нулевой вектор образует подпространство, называемое нулевым.Отметим также, что нулевой вектор всегда входит в любое подпространство. По закону контрпозиции из того, что нулевой элемент не входит в некоторое подмножество, следует, что это подмножество не является подпространством. Общий прием построения подпространств основан на понятии линейной оболочки системы векторов.

Определение. Линейной оболочкой 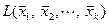системы векторов

называется множество всех линейных комбинаций этих векторов .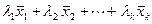

Как следует из определения, линейная оболочка 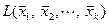является подпространством исходного линейного пространства. Чтобы подчеркнуть алгоритм построения линейной оболочки, ее часто называют подпространством, порожденным векторами , или линейной оболочкой, натянутой на векторы .

Линейная оболочка 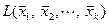является наименьшим подпространством, содержащим векторы . Действительно, это подпространство содержит векторы , из которых построена линейная оболочка 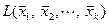. С другой стороны, всякое подпространство, содержащее векторы , обязано содержать и все линейные комбинации этих векторов.

Из доказанной выше теоремы о размерности пространства и его базисе следует, что если 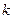векторов линейно независимы, то линейная оболочка 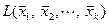является подпространством с размерностью .

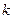Построим далее 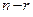решений однородной системы уравнений, полагая в общем решении вектор произвольных постоянных 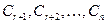равным векторам канонического базиса в пространстве арифметических векторов размерности :

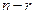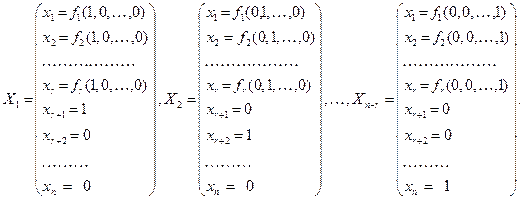
Эти вектор – решения линейно независимы, так как линейно независимы векторы канонического базиса размерности 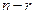, стоящие в нижних строках каждого из решений. Система вектор – столбцов решений 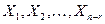называется фундаментальной системой решений однородной системы уравнений. Любая линейная комбинация этих решений

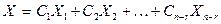
также является решением, так как по линейным свойствам матриц имеем:

=

=.

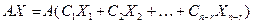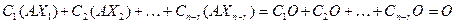Таким образом, мы построили множество решений однородной системы уравнений в виде линейной оболочки 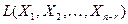, натянутой на фундаментальную систему решений. Так как решения 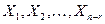представляют собой арифметические векторы длины 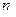и являются линейно независимыми, то размерность этой линейной оболочки равна 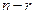. Другими словами, можно утверждать, что множество решений однородной системы с 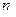неизвестными, есть подпространство размерности 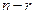пространства размерности .

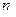Если мы возьмем любое решение 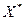однородной системы, то оно обязательно входит в линейную оболочку 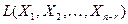. Действительно, рассмотрим разность между 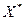и

решением 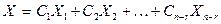из линейной оболочки .

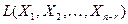Используя линейные свойства матриц, получим:

 

.

 

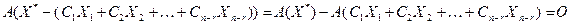Так как любая однородная система имеет тривиальное решение, то

 

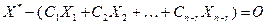и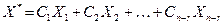

при некоторых значениях произвольных постоянных.

Таким образом, любое решение однородной системы уравнений 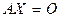всегда может быть представлено в виде линейной комбинации 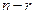произвольных постоянных и 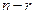фундаментальных решений, так что:

 

.

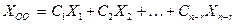Если задана произвольная неоднородная система , то для записи ее общего решения полезна следующая теорема.

Теорема (о виде общего решения неоднородной системы уравнений).

. Доказательство. Рассмотрим разность между любым решением неоднородной системы… .

ВЕКТОРНАЯ АЛГЕБРА

Под векторной алгеброй обычно понимают раздел линейной алгебры, изучающий геометрические векторы на плоскости и реальном пространстве. В математике… В данном разделе изучаются геометрические векторы на плоскости и реальном… Определение. Два линейных пространства и называются изоморфными, если между их элементами можно установить взаимно…

Евклидовы пространства.

Е1. Е2. Е3.

Таким образом, арифметическое пространствостановится евклидовым пространством, если определить скалярное произведение по указанному выше правилу.

Теорема (неравенство Коши – Буняковского ).

Доказательство.Если хотя бы один из двух векторов и нулевой, то доказываемое неравенство превращается в равенство и является справедливым. Рассмотрим далее случай, когда оба вектора , отличны от нулевого вектора. В… После того, как в линейном пространстве введено скалярное произведение, можно определить такие метрические понятия как…

Теорема (о линейной независимости ортогональной системы).

Всякая ортогональная система ненулевых векторов евклидова пространства является линейно независимой системой.

Доказательство.

Тогда, например, для произведения на первый вектор системы получим: Так как векторы системы ненулевые то и, следовательно, . Аналогично показывается, что и все остальные числовые…

Теорема Грама-Шмидта (о существовании ортонормированного базиса).

Доказательство.Согласно аксиоме размерности в пространстве имеется линейно независимая система из векторов . Покажем, что можно построить систему из… Доказательство проведем по методу математической индукции. 1. При утверждение теоремы очевидно. Если есть ненулевой вектор, то один нормированный вектор образует…

Теорема (основные свойства ортонормированного базиса).

2. Скалярное произведение двух любых векторов вычисляется в ортонормированном базисе как сумма произведений соответствующих координат в данном… Доказательство.Пусть есть некоторое разложение произвольного вектора в… для всех ,

Линейные пространства геометрических векторов на плоскости и реальном пространстве строятся, соответственно, на основе евклидовых пространств арифметических векторов и .

Определение.Любая упорядоченная пара точек 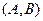называется направленным отрезком и обозначается как .

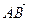Первый элемент пары – точку называют началом или точкой приложения направленного отрезка. Второй элемент пары – точку 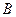называют окончанием направленного отрезка. Изображается направленный отрезок в виде стрелочки с началом в точке и окончанием в точке .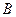

Будем говорить, что любые два направленных отрезка 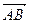и и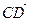меют одинаковую длину и направление, если равны арифметические векторы 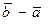и .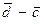

Определение. Геометрическим вектором 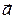называется множество всех направленных отрезков, имеющих одинаковую длину и направление.

О всяком направленном отрезке 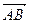из этого множества говорят, что он представляет геометрический вектор 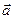(получен приложением вектора 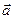к точке ). Каждому геометрическому вектору однозначно соответствует некоторый арифметический вектор, равный разностям компонент окончания и начала любого направленного отрезка, представляющего данный геометрический вектор.

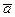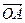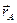Для любого арифметического вектора существует единственный направленный отрезок , который называют радиус - вектором точки и обозначают . Все направленные отрезки, имеющие одинаковую длину и направление с радиус – вектором 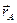образуют геометрический вектор 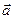. Таким образом, каждому арифметическому вектору 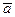соответствует единственный геометрический вектор 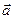, длина и направление которого задается этим арифметическим вектором.

Обратно, каждому геометрическому вектору 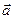соответствует единственный арифметический вектор 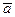, который определяет длину и направление любого направленного отрезка, составляющего этот геометрический вектор.

Иногда используют выражение «задан вектор 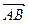». Это означает, что задан геометрический вектор, который полностью определяется арифметическим вектором . Радиус – вектор этого геометрического вектора равен 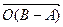, а любой направленный отрезок этого геометрического вектора с началом в произвольной точке 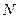равен .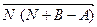

Геометрические векторы 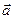и 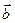называются равными 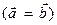, если множества представляющих их направленных отрезков совпадают. Два любых геометрических вектора равны тогда и только тогда, когда равны соответствующие им арифметические векторы. Как обычно, равенство понимается в том смысле, что слева и справа от знака равенства стоит один и тот же элемент, только записанный в различных формах.

Суммой 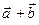двух любых геометрических векторов 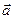и 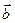называется геометрический вектор 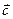, которому соответствует арифметический вектор 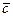с компонентами .

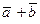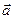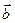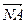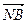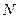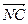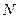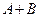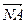Если геометрические векторы и представлены направленными отрезками и , имеющими общее начало , то их сумма представлена направленным отрезком . Этот направленный отрезок приложен к точке и имеет окончание в точке с координатами . На рисунке направленный отрезок изображается как диагональ параллелограмма, построенного на направленных отрезках и 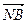. Сложение геометрических векторов по указанной схеме называют правилом параллелограмма.

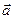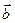Если геометрические векторы и представлены направленными отрезкам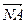и и 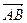, то их сумма представлена направленным отрезком 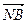. На рисунке направленный отрезок 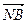изображается как стрелочка, идущая в треугольнике 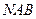от точки 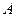к точке 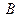. Сложение геометрических векторов по указанной схеме называют правилом треугольника.

Произведением числа 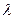на геометрический вектор 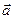называется геометрический вектор 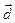, обозначаемый 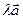, которому соответствует арифметический вектор .

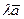Нулевой геометрический вектор обычно обозначается как 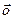и соответствует арифметическому вектору 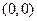или .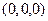

Ранее было показано, что для арифметических векторов любой размерности выполняются восемь аксиом линейного пространства. Так как основные операции для геометрических векторов введены посредством операций над двумерными и трехмерными арифметическими векторами, то для них также справедливы восемь аксиом линейного пространства. Таким образом, по построению, между геометрическими и арифметическими векторами одинаковой размерности установлено взаимно однозначное соответствие, согласованное с основными операциями вещественных линейных пространств, что позволяет считать геометрические векторы на плоскости и реальном пространстве конкретными векторами.

Как следует из общих определений, в арифметическом пространстве 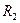скалярное произведение для любых двух векторов 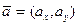и 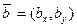определяется по формуле 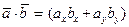. Соответственно, в арифметическом пространстве 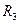скалярное произведение для любых двух векторов 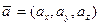и 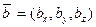определяется по формуле .

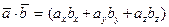Определение.Скалярным произведением геометрических векторов 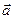, 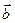называют скалярное произведение соответствующих арифметических векторов 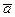,,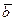 т.е. .

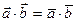Отсюда следует, что в пространстве геометрических векторов на плоскости скалярное произведение вычисляется по формуле 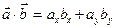, если заданы точк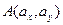и и 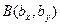. Аналогично, в реальном пространстве 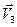скалярное произведение вычисляется по формуле 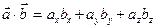, если заданы точки и .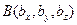

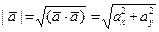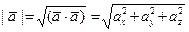Длину (модуль) арифметического вектора определяют и вычисляют, соответственно, по формулам для и для .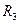

Определение.Длиной (модулем) геометрического вектора 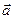называют длину, соответствующего ему арифметического вектора .

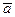Так, если геометрический вектор 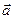в реальном пространстве задан арифметическим вектором 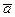с компонентами 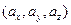, то длина вектора 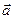находится по формуле

.

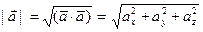В частности, нулевой геометрический вектор 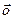имеет нулевую длину.

Если, например, геометрический вектор 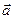представлен направляющим отрезком 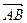в реальном пространстве, то ему соответствует арифметический вектор 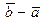, и его длину в этом случае находят по формул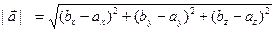е , где 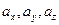есть компоненты арифметического вектора 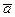и 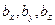есть компоненты вектора .

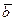Длину направленного отрезка 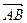обозначают 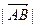и определяют по формуле 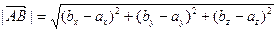. Отметим, что длина направленного отрезка равна расстоянию 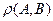между точками и .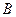

Модуль произведения числа 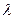на геометрический вектор 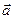находится по формуле 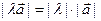, что следует непосредственно из приведенных формул. Если число 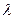строго положительно, то вектор 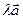имеет то же направление, что и вектор 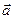. Если число 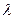строго отрицательно, то вектор 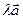имеет то же направление, что и вектор 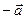, то есть, направлен в противоположную сторону.

Определение.Угол между двумя любыми ненулевыми геометрическими векторам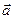и и 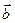определяется по формуле .

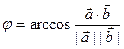В частности, в реальном пространстве .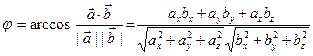

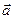В задачах, где известен угол между векторами и 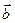и длины этих векторов, скалярное произведение вычисляют по формуле .

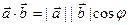Определение.

Как следует из определения векторы образуют ортонормированный базис. Определение.Числовой проекцией вектора на вектор называют число, найденное как… Как следует из определения, числовые проекции вектора на векторы канонического базиса совпадают с компонентамивектора…

Векторное и смешанное векторно-скалярное произведения.

При решении практических задач, представление вектора в каноническом базисе находят, формально раскрывая по первой строке определитель третьего… Отметим, что векторное произведение, в отличие от скалярного произведения,… Непосредственно из определения следуют алгебраические свойства векторного произведения: ; ; .

Теорема (условие равенства векторного произведения нулевому вектору).

Доказательство.Если хотя бы один из векторов , равен нулевому вектору , то векторное произведение также равно нулевому вектору. В том случае, когда оба вектора ,отличны от нулевого и являются коллинеарными,… Для доказательства необходимости условия теоремы, предположим, что векторное произведение равно нулевому вектору. Из…

Теорема (о модуле векторного произведения ).

Доказательство.Если векторы , являются коллинеарными, то их векторное произведение равно нулевому вектору, а модуль нулевого вектора равен нулю. Так… Таким образом, доказываемая формула справедлива для коллинеарных векторов. Пусть векторы и не являются коллинеарными.

Таким образом, смешанное произведение трех компланарных (лежащих в одной плоскости) векторов равно нулю.

Основное алгебраическое свойство смешанного произведения состоит в том, что циклическая перестановка векторов, не меняет его величины, т.е. , что проверяется непосредственно по определяющей формуле.

Линейные геометрические объекты.

При прямая проходит через нулевой вектор пространства и представляет собой линейную оболочку направляющего вектора . Как и любая линейная оболочка… В общем случае, при , прямая получается из линейного подпространства сдвигом… Определение.Любое подмножество линейного пространства, полученное путем сдвига на некоторый фиксированный вектор,…

ЛИНЕЙНЫЕ ОПЕРАТОРЫ И ИХ МАТРИЦЫ

Линейным операторомв линейном пространстве 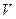называется всякое отображение 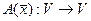пространства 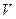в себя, обладающее линейными свойствами

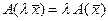и .

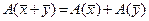Например, в пространстве трехмерных арифметических векторов, проектирование на плоскость 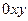, задаваемое по правилу

,

является линейным оператором, что проверяется непосредственно по определению.

Единичный оператор 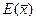, реализующий тождественное отображение пространства 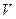на себя, также является линейным оператором.

Множество элементов линейного пространства 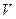, которые являются образами векторов из области определения 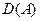оператора, называют образом оператора 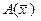и обозначают .

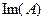Ядром линейного оператора называют множество элементов линейного пространства 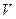, образом которых является нулевой элемент. Ядро оператора обозначают .

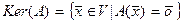В дальнейшем мы будем рассматривать линейные операторы, заданные только в конечномерных линейных пространствах.

Непосредственно из определений следует, что и образ, и ядро оператора являются линейными подпространствами. При этом размерность образа оператора 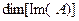называют рангом оператора 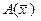и обозначают 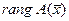. Размерность ядра оператора 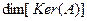называют дефектом оператора и обозначают .

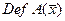Доказано, что сумма ранга и дефекта оператора равна размерности пространства, в котором действует оператор:

.

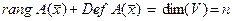Пусть 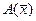- произвольный линейный оператор в -мерном линейном пространстве с некоторым фиксированным базисом 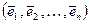. Разложим преобразованные векторы базиса 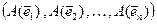по исходному базису:

.

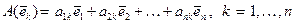Квадратная матрица, составленная из коэффициентов этого разложения

,

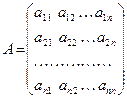называется матрицей оператора 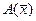в заданном фиксированном базисе.

По теореме о единственности разложения векторов по базису, каждому линейному оператору соответствует единственная матрица оператора в фиксированном базисе. Отметим, что, выбрав другой базис в линейном пространстве, мы получили бы другую матрицу для того же оператора.

Обратно, если задана некоторая произвольная квадратная матрица и фиксирован некоторый базис 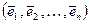, то этой матрице соответствует единственный линейный оператор 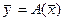, действующий по правилу 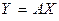, где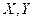- столбцы координат векторов 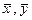в указанном базисе. Таким образом, между линейными операторами и матрицами имеется взаимно однозначное соответствие для любого фиксированного базиса.

Доказано, что ранг линейного оператора и ранг матрицы оператора всегда совпадают, причем независимо от выбора базиса в исходном векторном пространстве .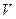

Число 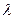называется собственным значением, а ненулевой вектор 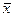-соответствующимэтому числу собственным векторомлинейного оператора, если они связаны между собой соотношением

.

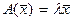В -мерном линейном пространстве с некоторым базисом 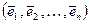векторное равенство 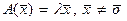равносильно матричному равенству 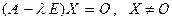. Для того чтобы найти собственные векторы, следует найти ненулевые решения однородной системы уравнений

.

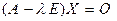Такие решения существуют только в том случае, когда ранг матрицы строго меньше числа неизвестных 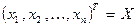. Отсюда следует, что .

Уравнение относительно неизвестного 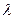называют характеристическим уравнением линейного оператора, а полином 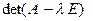степени называют характеристическим полиномом оператора.

Как известно, полином степени имеет ровно вещественных или комплексных корней с учетом их кратности. Таким образом, решив уравнение , мы получим систему чисел 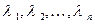. Некоторым из этих чисел 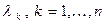соответствуют бесконечные множества ненулевых собственных векторов, выделяемые из общего решения однородной системы уравнений . Множество всех таких собственных чисел называют спектром линейного оператора.

Доказано, что спектр линейного оператора не зависит от выбора базиса.

Найдем, для примера, собственные значения и собственные векторы линейного оператора 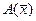, заданного с помощью следующей матрицы оператора

.

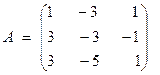Составим характеристическое уравнение оператора

.

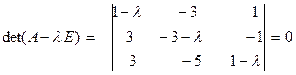Раскрывая определитель по правилу Саррюса, получим кубическое уравнение относительно неизвестного 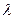: 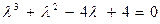. Это уравнение имеет три вещественных корня, которые нумеруют в порядке убывания с учетом кратности .

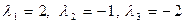Для каждого значения составляются однородные системы уравнений относительно неизвестных : .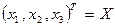

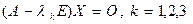Для 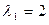однородная система имеет вид: .

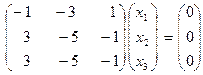Преобразуем матрицу коэффициентов нашей системы в соответствии с прямым ходом метода Гаусса .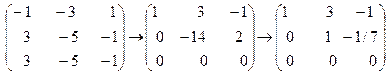

 

Ранг преобразованной матрицы равен двум, поэтому имеем два базисных неизвестных и одно свободное неизвестное 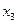. Полагаем свободное неизвестное равным произвольной постоянной: 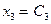. Неизвестные находим из системы уравнений, соответствующей преобразованной матрице, в виде .

Отбрасывая из общего решения однородной системы нулевое решение, бесконечное множество собственных векторов линейного оператора обычно записывают или в строку в виде 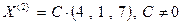, или в столбец в виде .

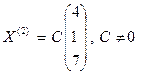Здесь символом 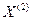обозначена переменная, принимающая возможные значения собственных векторов, отвечающих собственному значению два; буквой 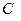- произвольная постоянная, принимающая любые ненулевые вещественные значения, 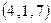- один из удобных собственных векторов, записанный в строку и полученный из общего решения при .

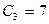Аналогично, составляются однородные системы уравнений для двух других корней характеристического уравнения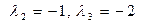. Эти системы исследуются по методу Гаусса. В нашем случае обе системы имеют нетривиальные решения, что позволяет получить множества собственных векторов, отвечающих этим числам, в следующем виде:

 

, .
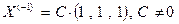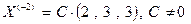