Дифференциальные зависимости между

Сурьянинов Н.Г.

МЕТОДЫ ПОСТРОЕНИЯ ЭПЮР В СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМАХ

 

 

Одесса - 2001

Содержание

Содержание................................................................................................................................................................................... 2

Введение.......................................................................................................................................................................................... 4

Глава 1 Построение эпюр внутренних силовых факторов............................................................. 5

1.1 Внутренние силы упругости. Метод сечений............................................................................................ 5

1.2 Виды сопротивлений.......................................................................................................................................... 7

1.3 Виды опорных закреплений.............................................................................................................................. 8

1.4 Построение эпюр продольных сил 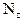......................................................................................................... 9

1.4 Построение эпюр крутящих моментов 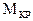........................................................................................... 10

1.5 Правила контроля эпюр 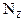и 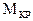........................................................................................................... 12

1.6 Построение эпюр поперечных сил и изгибающих моментов в балках.............................. 12

1.7 Консольные балки.............................................................................................................................................. 13

1.8 Дифференциальные зависимости между 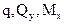............................................................................. 15

1.9 Балки на двух опорах........................................................................................................................................ 17

1.10 Правила контроля эпюр Q_у и M_x.................................................................................................................. 20

1.11 Другие подходы к построению эпюр внутренних силовых факторов.............................................. 21

1.12 Построение эпюр для плоских рам............................................................................................................. 22

1.13 Рамы с жесткой заделкой............................................................................................................................ 25

1.14 Рамы на двух шарнирных опорах................................................................................................................ 29

1.15 Рамы на двух опорах с промежуточным шарниром............................................................................. 35

1.16 Построение эпюр в плоско-пространственных системах.................................................................. 38

1.17 Построение эпюр в ломаных стержнях.................................................................................................... 45

Глава 2 Определение перемещений в упругих системах.............................................................. 52

2.1 Обобщенные силы и обобщенные перемещения........................................................................................ 53

2.2 Работа внешних сил. Потенциальная энергия........................................................................................... 54

2.3 Теорема о взаимности работ........................................................................................................................ 58

2.4 Теорема о взаимности перемещений........................................................................................................... 60

2.5 Вычислений перемещений методом Мора.................................................................................................. 61

Примеры расчетов................................................................................................................................................... 64

2.7 Правило Верещагина........................................................................................................................................ 68

2.8 Основные варианты перемножения эпюр................................................................................................. 70

Глава 3 Построение эпюр в статически неопределимых истемах. Метод сил.......... 78

3.1 Особенности статически неопределимых систем и методы их расчета........................................ 78

3.2 Канонические уравнения метода сил........................................................................................................... 80

3.3 Алгоритм расчета методом сил................................................................................................................... 82

3.4 Выбор основной системы............................................................................................................................... 83

3.5 Вычисление коэффициентов и свободных членов канонических уравнений..................................... 85

3.6 Универсальная проверка коэффициентов и свободных членов канонических уравнений............ 86

3.7 Построение окончательных эпюр внутренних силовых факторов.................................................... 88

3.8 Проверка окончательной эпюры изгибающих моментов...................................................................... 89

3.9 Определение перемещений в статически неопределимых системах................................................ 90

3.10 Расчет симметричных систем методом сил......................................................................................... 91

3.10 Примеры расчетов......................................................................................................................................... 93

Глава 4 Построение эпюр в статически неопределимых системах. Метод перемещений 119

4.1 Сущность метода........................................................................................................................................... 119

4.2 Вспомогательная таблица метода перемещений................................................................................ 123

4.3 Каноническое уравнение метода перемещений..................................................................................... 130

4.4 Алгоритм расчета систем методом перемещений.............................................................................. 133

4.5 Методы вычисления коэффициентов и свободных членов канонических уравнений.................. 133

4.6 Проверки метода перемещений................................................................................................................ 134

4.7 Использование симметрии при расчете рам методом перемещений............................................. 137

4.8 Примеры расчетов......................................................................................................................................... 138

Литература:................................................................................................................................................................. 155

Введение

Эта книга в значительной степени соответствует курсу лекций, на протяжении многих лет читаемых в Одесском государственном политехническом университете для студентов механических специальностей.

Книга состоит из четырех глав, в которых достаточно подробно рассматриваются методы построения эпюр внутренних силовых факторов статически определимых и статически неопределимых стержневых системах.

В большинстве изданных учебников и учебных пособий этот важнейший вопрос излагается поверхностно, или вообще отсутствует.

В главе 1 рассматривается построение эпюр в различных стержневых системах: балках, рамах, плоскопространственных и др.

В главе 2 приводятся различные общие методы определения перемещений, что имеет самостоятельное значение, а также является базой для двух последующих глав.

В главе 3 дается подробное изложение метода сил применительно к расчету статически неопределимых балок и рам. Рассмотрены все проверки метода, а также использование симметрии.

Глава 4 посвящена изложению метода перемещений. Приведенный здесь материал в лекционном курсе, как правило, не излагается в связи с ограниченностью во времени. Тем не менее метод перемещений очень важен, так как, во-первых, является мощным инструментом для расчета статически неопределимых систем, а во-вторых, используется студентами механических специальностей в дисциплинах, читаемых на старших курсах.

Книга снабжена большим количеством примеров.

Глава 1 Построение эпюр внутренних силовых факторов

Внутренние силы упругости. Метод сечений

Эти дополнительные силы взаимодействия называются внутренними силами упругости (ВСУ) и являются предметом изучения сопротивления материалов. Анализ характера распределения внутренних сил упругости осуществляется при…

Виды сопротивлений

Растяжение (или сжатие) - это вид сопротивления, при котором во всех поперечных сечениях возникает только продольная сила . Кручение - это вид сопротивления, при котором во всех поперечных сечениях… Чистый изгиб - это вид сопротивления, при котором во всех поперечных сечениях возникает только изгибающий момент…

Виды опорных закреплений

Рис. 3 В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает…

Консольные балки

Пример 3. Построить эпюры и (рис.6). Рис. 6

Балки на двух опорах

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная… Условие используется для проверки вычисленных значений опорных реакций.

Другие подходы к построению эпюр внутренних силовых факторов

Другой возможный подход состоит в том, что балка разбивается на участки (с распределенными нагрузками и между точками приложения сил и моментов).… Очевидно, что при обоих подходах в конечном счете все сводится к вычислению… Правда, следует отметить, что запись общих выражений как функций от z удобна при программировании построения эпюр при…

Построение эпюр для плоских рам

Вертикально (или под наклоном) расположенные стержни рамы называются стойками, а горизонтальные - ригелями. Жесткость узлов устраняет возможность… Как и многие другие системы, рамы делятся на статически определимые и… Промежуточный шарнир снижает степень статической неопределимости рамы на величину m - 1, где m - число стержней,…

Пример 7.

Рассмотрим жесткозащемленную плоскую раму (рис.11,а). В жесткой заделке рамы в общем случае нагружения возникают три опорные реакции: две силы (и ) и опорный момент (). Для построения эпюр определение этих реакций не является безусловной необходимостью: расчет, как и в случае жесткозащемленной балки, можно вести от свободного конца, то есть всякий раз так выбирать отсеченную часть для рассматриваемого сечения, чтобы в нее не попадала опора с неизвестными опорными реакциями. Тем не менее, иногда целесообразно вычислить опорные реакции. Это позволяет проверить построение эпюр или облегчить их построение. Для вычисления реакций в жесткозащемленной раме используются три условия равновесия:

Построим эпюры 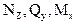для рассматриваемой рамы, не вычисляя опорные реакции.

Методика построения эпюр аналогична ранее рассмотренной для балок , т.е. сначала необходимо наметить характерные сечения. В дополнение к ранее указанным (см.1.2), в рамах характерными являются также сечения, расположенные бесконечно близко к жесткому узлу на всех элементах, сходящихся в этом узле.

Построение эпюры 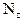. Следуя установленным правилам, в рассматриваемой раме можно выделить 8 характерных сечений. Продольная сила в любом из них численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня. При этом следует учитывать, что положение продольной оси будет изменяться в зависимости от того, чему принадлежит рассматриваемое сечение - стойкам или ригелю.

Построение эпюры 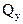. Поперечная сила в любом сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную ось рамы. Положение поперечной оси также будет изменяться в зависимости от принадлежности данного сечения стойкам или ригелю. С учетом правила знаков, двигаясь от свободного конца к жесткой заделке, получим для :

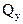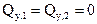(проекция пары М на любую ось равна нулю);

Необходимо обратить внимание на тот факт, что , т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.

Построение эпюры . Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех нагрузок, приложенных по одну сторону от рассматриваемого сечения, относительно этого сечения (более строго: относительно оси x этого сечения). Обратим внимание на два важных замечания:

1) составляющая момента от действия сосредоточенного момента М всегда одинакова и равна М;

2) под плечом силы всегда понимается длина перпендикуляра, опущенного из центра тяжести данного сечения на линию действия силы. Это означает, что, например, плечо силы F для сечений 4-7 одинаково и равно 3 м.

Рис. 11

Таким образом, для сечений 1-8 получим:

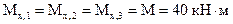(сжатым является правое волокно в сечениях 1-3, поэтому ордината отложена вправо от оси стойки);

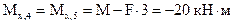(знаки "+" и "-" здесь имеют относительный характер; результирующий момент сжимает левые волокна в сечении 4 и нижние волокна в сечении 5, поэтому ордината "20" откладывается соответственно влево и вниз);

(сжаты нижние волокна);

(сжаты правые волокна);

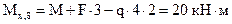(сжаты левые волокна).

Между в плоских рамах сохраняются те же зависимости, что и в балках, а именно:

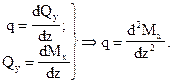
Из этого следует, что правила контроля эпюр 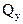и остаются теми же, что и для балок ,( см. 1.11).

Эпюры 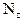в плоских рамах строятся наиболее просто и при отсутствии нагрузок, распределенных вдоль стержней, представляют собой графически отрезки прямых, параллельные осям стержней ( или совпадают с ними при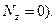

Если проанализировать процесс построения эпюр (рис.11,б-г), то очевидно, что наиболее "сложно" вычислять ординаты в сечениях стержня, примыкающего к заделке ( на рис.11,б-г это сечения 7 и 8). Как уже отмечалось, с этой целью иногда вычисляют реакции и момент .

При принятом для всей рамы направлении осей 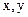(рис.11,а) уравнения равновесия имеют вид:

Полученный для каждой из величин знак "+" говорит, что направления их были выбраны правильно.

После вычисления опорных реакций значения величин 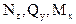в сечениях 7 и 8 (как, впрочем, и в любом другом) можно вычислять, двигаясь от жесткой заделки к свободному концу.

Например, для сечений 7 и 8:

(знак "-" указывает на сжатие в этих сечениях с силой );

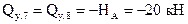(т.к. реакция стремится повернуть каждое из этих сечений против часовой стрелки.)

При сравнении величины 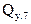с ранее полученной величиной 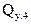видно, что

, о чем уже говорилось выше.

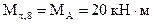(сжаты левые волокна стойки);

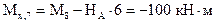(сжаты правые волокна стойки).

Разумеется, результаты получаемые для любого сечения при движении от свободного конца к жесткой заделке и при движении в обратном направлении одинаковы.

Рамы на двух шарнирных опорах

В дальнейшем для краткости будем говорить "шарнирная рама", имея в виду ее статическую определимость и отсутствие промежуточных шарниров ( см. 1.13).

Пример 8.

Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.12,а).

Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.

Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:

Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.

Так, в рассматриваемом примере этим условием будет 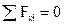, которое будет содержать неизвестную реакцию (в то время как условие 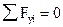содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие .

Рис. 12

Второе и третье уравнения равновесия (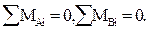) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения ( иногда - с нулевым плечом).

В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть .

Построение эпюр 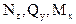в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.

Вычислим реакции опор рамы (рис.12,а)

Уравнения статики:

Знак "-", полученный при вычислении реакции , говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:

,

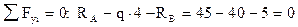то есть реакции опор вычислены правильно.

Построение эпюры .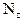

Двигаясь по оси рамы от сечения 1 к сечению 6, получим:

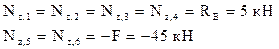
Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:

Этот же результат получим из рассмотрения отсеченной части 1-6:

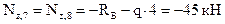
Этот же результат получим из рассмотрения отсеченной части 1-6:

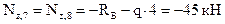
По вычисленным значениям строим эпюру 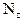( рис.12,б)

Построение эпюры .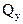

Из рассмотрения отсеченной части 1-5:

Из рассмотрения отсеченной части 8-6:

Эпюра 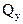, построенная по вычисленным значениям, показана на рис.12,в.

Построение эпюры .

Из рассмотрения отсеченной части 1-5:

(сжаты правые волокна стойки);

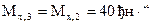(плечо силы F равно нулю);

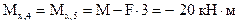(сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);

Из рассмотрения отсеченной части 8 -6:

(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).

Эпюра показана на рис12,г.

Пример 9. Рассмотрим шарнирную раму более сложной конфигурации (рис.13,а).

Здесь необходимо рассматривать 10 характерных сечений для построения эпюр 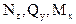. Сечения 1-6 расположены на ригеле слева направо, а сечения 7-10 - на стойке сверху вниз. Как и в предыдущем примере, указанное расположение характерных сечений является безусловно необходимым, а их нумерация - произвольной.

Уравнения статики для вычисления опорных реакций имеют вид:

Проверка вычисления опорных реакций:

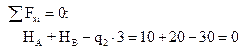
При построении эпюр 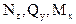целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.

Рис. 13

Построение эпюр .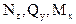

Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):

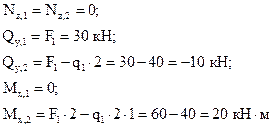(сжаты верхние волокна).

Из рассмотрения правой отсеченной части (сечения 3-6):

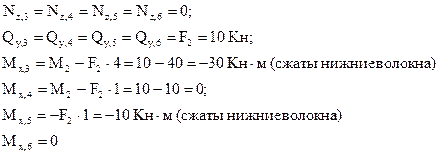
Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):

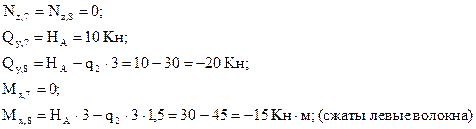
Из рассмотрения нижней отсеченной части (сечения 9-10):

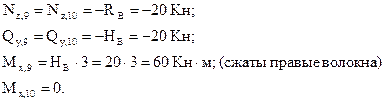
Характер эпюры 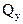на участках рамы с распределенными нагрузками и 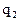, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент принимает экстремальные значения. Определение положений точек пересечения (т.е. тех точек, где 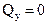) выполняется так же, как и в балках (см. 1.9).

Вычислим экстремальные значения момента .

На участках под распределенной нагрузкой :

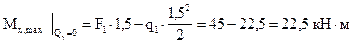(сжаты верхние волокна).

На участке с распределенной нагрузкой :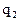

(сжаты правые волокна).

Эпюры 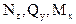показаны на рис.13,б,в,г.

Рамы на двух опорах с промежуточным шарниром

Пример 10. Рассмотрим построение эпюр для рамы с промежуточным шарниром (рис.14,а) В дополнение к условиям равновесия, рассмотренным в примерах 8 и 9, здесь для… Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще…

Построение эпюр в плоско-пространственных системах

В настоящем пособии будем рассматривать только жесткозащемленые плоско-пространственные системы (далее сокращенно: ППС). При этом возможны два… 1) система располагается горизонтально, нагрузки приложены в вертикальных… 2) система располагается в вертикальной плоскости, нагрузки приложены горизонтально (рис.15,в,г)

Построение эпюр в ломаных стержнях

Рис.17 В общем случае нагружения в поперечных сечениях ломаных стержней могут возникать все 6 известных внутренних силовых…

Глава 2 Определение перемещений в упругих системах

Любая конструкция под действием приложенных внешних нагрузок изменяет в той или иной степени свою форму и размеры – деформируется. Для проверки жесткости и устойчивости конструкции необходимо уметь определять перемещения, вызванные деформацией ее элементов. Кроме того, определение перемещений конструкции является важнейшей вспомогательной задачей при расчете статически неопределимых систем.

Методы определения этих перемещений весьма разнообразны. Они отличаются друг от друга главным образом степенью сложности и областью применения.

Исторически первым предложенным методом определения перемещений можно считать метод непосредственного интегрирования дифференциального уравнения упругой линии балки. Однако в случае балок с большим количеством участков реализация этого метода сопряжена со значительными трудностями, которые заключаются не в интегрировании дифференциальных уравнений, а в технике определения произвольных постоянных интегрирования – составлении и решении систем линейных алгебраических уравнений.

Если по условиям нагружения балка разбивается на n участков, то задача становится очень трудоемкой уже при n=3. Для уменьшения большого объема вычислительной работы, связанной с определением произвольных постоянных интегрирования, разработан ряд методов, из которых, прежде всего, отметим метод начальных параметров, позволяющий при любом числе участков свести решение к отысканию только двух постоянных – прогиба и угла поворота в начале координат.

Указанные методы, как и некоторые другие, носят частный характер. С некоторой натяжкой их можно признать удобными при решении ограниченного круга простейших задач.

Наиболее общим методом определения перемещений в стержневых системах является метод Мора (иногда говорят: Максвелла – Мора), в основе которого лежат два основных принципа механики: начало возможных перемещений и закон сохранения энергии. Прежде чем перейти к изложению метода, остановимся на его основных теоретических предпосылках.

Обобщенные силы и обобщенные перемещения

В задачах механики внешняя нагрузка отличается большим разнообразием и обычно представляет собой группы сил. Выражения для какой-либо группы… , (2.1) одна из которых – F – зависит только от сил группы и называется обобщенной силой, а другая - - зависит от перемещений…

Работа внешних сил. Потенциальная энергия

  Рис. 20

Теорема о взаимности работ

Рис. 23 Обозначим работу нагрузки первого состояния (сила F1) на перемещениях первого состояния через А11, а работу силы F2 на…

Теорема о взаимности перемещений

На основании теоремы о взаимности работ: , но , поэтому , или в общем случае действия любых единичных сил: (2.16)

Вычислений перемещений методом Мора

Рассмотрим два состояния системы. Пусть в первом из них (грузовое состояние) к балке приложена любая произвольная нагрузка, а во втором (единичное… Работа А21 силы на перемещении , возникающем от сил первого состояния: .

Примеры расчетов

Пример 13. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.26,а), методом Мора.

Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов 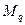(рис.26,б). Второе состояние (единичное) – при действии сосредоточенной силы 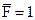, приложенной в точке С; ему соответствует эпюра моментов

(рис.26,в). Третье состояние (также единичное) – при действии сосредоточенного момента 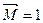, приложенного в точке В; ему соответствует эпюра моментов (рис.26,г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:

Вычисляем прогиб балки в точке С:

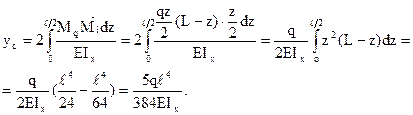
Знак "+" означает, что точка С переместится в направлении действия силы.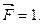

Вычисляем угол поворота сечения В:

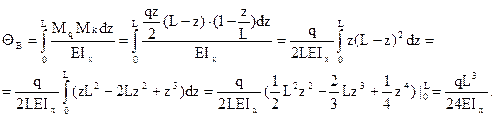
Рис. 26

Рис. 27

Знак "+" означает, что сечение В поворачивается в направлении действия момента то есть по часовой стрелке.

Пример 14. Определить прогиб балки в середине пролета (рис.27,а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба.

Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.27,а); ему соответствует эпюры изгибающих моментов(рис.27,б) и поперечных сил 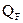(рис.27,в).

Второе состояние (единичное) – при действии силы (рис.27,г); ему соответствуют эпюры изгибающих моментов (рис.27,д) и поперечных сил 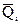(рис.27,е).

В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (2.18) принимает вид:

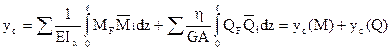
Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.27) для составляющих полного перемещения получим:

Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h, при этом h=0,1ℓ.

Тогда площадь сечения и его осевой момент инерции равны:

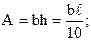
Будем считать, что 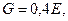тогда:

то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения 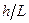влияние поперечных сил на величину прогиба становится еще менее значительным.

Правило Верещагина

Оказывается, что от этого недостатка можно уйти, если непосредственное интегрирование в формулах Мора заменить так называемым перемножением эпюр.… Способ вычисления интеграла Мора путем замены непосредственного интегрирования… Докажем справедливость этого правила. Рассмотрим две эпюры (рис.28). Пусть одна из них (Mn) является грузовой и имеет…

Основные варианты перемножения эпюр

Очевидно, что разнообразие приложенных нагрузок и геометрических схем конструкций приводит к различным, с точки зрения геометрии, перемножаемым эпюрам. Для реализации правила Верещагина нужно знать площади геометрических фигур и координаты их центров тяжести. На рис.29 представлены некоторые основные варианты, возникающие в практических расчетах.

Для перемножения эпюр сложной формы их необходимо разбивать на простейшие. Например, для перемножения двух эпюр, имеющих вид трапеции, нужно одну из них разбить на треугольник и прямоугольник, умножить площадь каждого из них на ординату второй эпюры, расположенную под соответствующим центром тяжести, и результаты сложить. Аналогично поступают и для умножения криволинейной трапеции на любую линейную эпюру.

Если указанные выше действия проделать в общем виде, то получим для таких сложных случаев формулы, удобные для использования в практических расчетах (рис.30). Так, результат перемножения двух трапеций (рис.30,а):

(2.21)

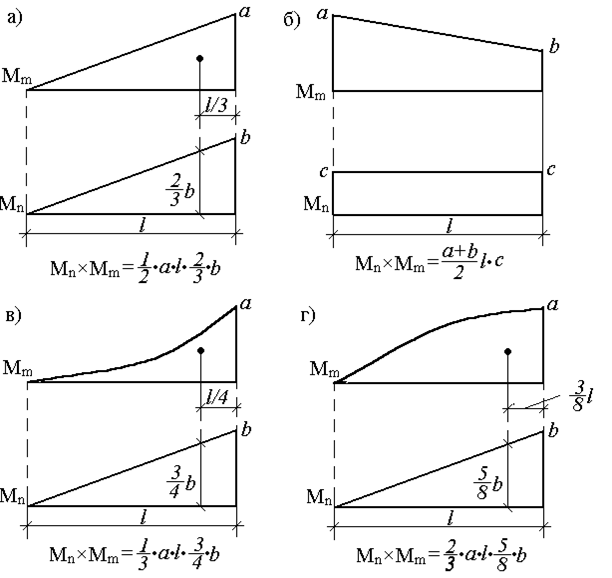
Рис. 29

По формуле (2.21) можно перемножить и эпюры, имеющих вид "перекрученных" трапеций (рис.30,б), но при этом произведение ординат, расположенных по разные стороны от осей эпюр, учитывается со знаком минус.

Если одна из перемножаемых эпюр очерчена по квадратной параболе (что соответствует нагружению равномерно распределенной нагрузкой), то для перемножения со второй (обязательно линейной) эпюрой ее рассматривают как сумму (рис.30,в) или разность (рис.30,г) трапециидальной и параболической эпюр. Результат перемножения в обоих случаях определяется формулой:

(2.22)

но значение f при этом определяется по-разному (рис. 30, в, г).

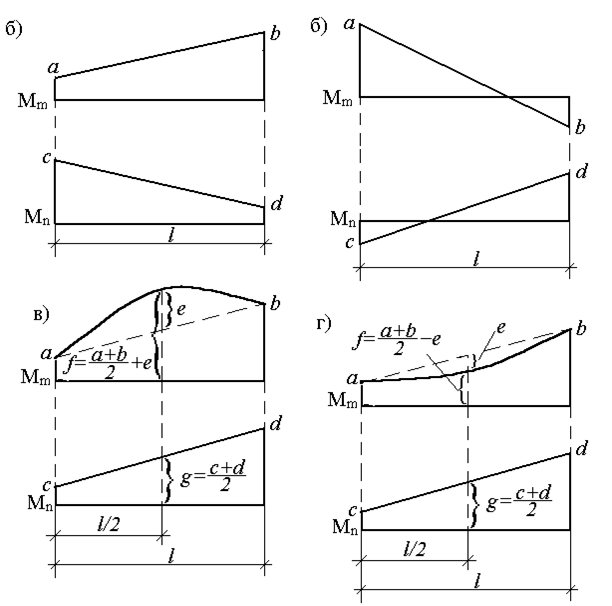
Рис. 30

Возможны случаи, когда ни одна из перемножаемых эпюр не является прямолинейной, но хотя бы одна из них ограничена ломаными прямыми линиями. Для перемножения таких эпюр их предварительно разбивают на участки, в пределах каждого из которых по крайней мере одна эпюра являетя прямолинейной.

Рассмотрим использование правила Верещагина на конкретных примерах.

Пример 15. Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.31,а), способом Верещагина.

Последовательность расчета способом Верещагина – такая же, как и в методе Мора, поэтому рассмотрим три состояния балки: грузовое – при действии распределенной нагрузки q; ему соответствует эпюра M_q (рис.31,б), и два единичных состояния - при действии силы приложенной в точке С (эпюра 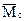, рис.31,в), и момента 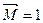, приложенного в точке В (эпюра 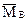, рис.31,г).

Прогиб балки в середине пролета:

.

Аналогичный результат был получен ранее методом Мора (см. пример 13). Следует обратить внимание на тот факт, что перемножение эпюр выполнялось для половины балки, а затем, в силу симметрии, результат удваивался. Если же площадь всей эпюры M_q умножить на расположенную под ее центром тяжести ординату эпюры 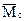(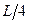на рис.31,в), то величина перемещения будет совершенно иной и неправильной так как эпюра 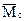ограничена ломаной линией. На недопустимость такого подхода уже указывалось выше.

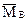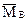А при вычислении угла поворота сечения в точке В можно площадь эпюры M_q умножить на расположенную под ее центром тяжести ординату эпюры (, рис.31,г), так как эпюра ограничена прямой линией:

Этот результат также совпадает с результатом, полученным ранее методом Мора (см. пример 13).

 

Рис. 31

 

Пример 16. Определить горизонтальное и вертикальное перемещения точки А в раме (рис.32,а).

Как и в предыдущем примере, для решения задачи необходимо рассмотреть три состояния рамы: грузовое и два единичных. Эпюра моментов M_F, соответствующая первому состоянию, представлена на рис.32,б. Для вычисления горизонтального перемещения прикладываем в точке А по направлению искомого перемещения (т.е. горизонтально) силу 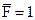, а для вычисления вертикального перемещения силу 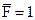прикладываем вертикально (рис.32,в,д). Соответствующие эпюры и показаны на рис.32,г,е.

Горизонтальное перемещение точки А:

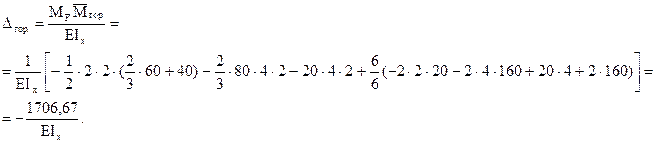
При вычислении на участке АВ трапеция (эпюра M_F) разбита на треугольник и прямоугольник, после чего треугольник с эпюры "умножен" на каждую из этих фигур. На участке ВС криволинейная трапеция разделена на криволинейный треугольник и прямоугольник, а для перемножения эпюр на участке СД использована формула (2.21).

Знак " - ", полученный при вычислении , означает, что точка А перемещается по горизонтали не влево (в этом направлении приложена сила 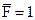), а вправо.

Вертикальное перемещение точки А:

Здесь знак " - " означает, что точка А перемещается вниз, а не вверх.

Отметим, что единичные эпюры моментов, построенные от силы 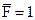, имеют размерность длины, а единичные эпюры моментов построенные от момента , являются безразмерными.

Рис.32

Пример 17. Определить вертикальное перемещение точки А плоско-пространственной системы (рис.33,а).

Рис.23

Как известно (см. гл.1), в поперечных сечениях стержней плоско-пространственной системы возникают три внутренних силовых фактора: поперечная сила Q_y, изгибающий момент M_x и крутящий момент M_кр. Так как влияние поперечной силы на величину перемещения незначительно (см. пример 14, рис.27), то при вычислении перемещения методом Мора и Верещагина из шести слагаемых остаются только два.

Для решения задачи построим эпюры изгибающих моментов M_x,q и крутящих моментов М_кр,q от внешней нагрузки (рис.33,б), а затем в точке А приложим силу 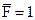по направлению искомого перемещения, т.е. вертикального (рис.33,в), и построим единичные эпюры изгибающих моментов и крутящих моментов 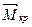(рис.33,г). Стрелками на эпюрах крутящих моментов показаны направления закручивания соответствующих участков плоско-пространственной системы.

Вертикальное перемещение точки А:

При перемножении эпюр крутящих моментов произведение берется со знаком "+", если стрелки, указывающие направление кручения, сонаправленны, и со знаком " - " – в противном случае.

Глава 3 Построение эпюр в статически неопределимых истемах. Метод сил

Особенности статически неопределимых систем и методы их расчета

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а… Статически неопределимые системы обладают рядом характерных особенностей: 1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как…

Канонические уравнения метода сил

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе,… Условие равенства нулю перемещения по направлению любой i-ой связи из n… (3.1)

Алгоритм расчета методом сил

1. Определить степень статической неопределимости. 2. Выбрать основную систему. 3. Сформировать эквивалентную систему.

Выбор основной системы

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в… 2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом… 3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.35,в). В частных случаях…

Вычисление коэффициентов и свободных членов канонических уравнений

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех… Единичные и грузовые перемещения (коэффициенты и свободные члены канонических…

Универсальная проверка коэффициентов и свободных членов канонических уравнений

Перемножим суммарную единичную эпюру с эпюрой

Построение окончательных эпюр внутренних силовых факторов

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все… , или, учитывая, что

Проверка окончательной эпюры изгибающих моментов

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных… Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части… Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть…

Определение перемещений в статически неопределимых системах

(3.13) где М – эпюра изгибающих моментов от внешней нагрузки, построенная для… Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически…

Расчет симметричных систем методом сил

Основным средством для достижения этой цели является использование симметрии. Стержневая система является симметричной, если симметричны не только… При выборе основной системы лишние неизвестные следует выбирать в виде… (3.14)

Примеры расчетов

Рассмотрим приведенный выше алгоритм расчета различных систем методом сил на конкретных примерах статически неопределимых балок и плоских рам.

Пример 18. Построить эпюру изгибающих моментов для статически неопределимой балки (рис.36,а).

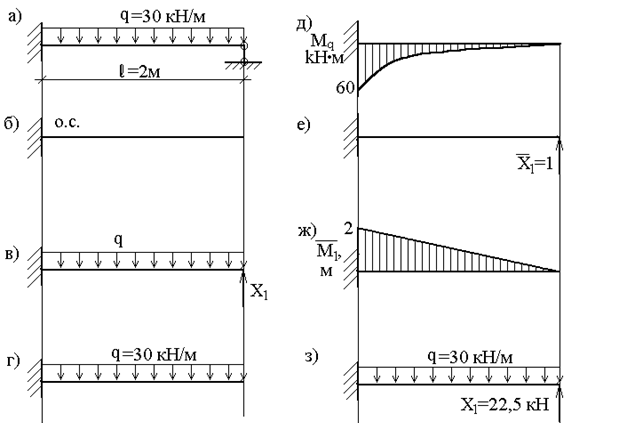
Рис. 36

Степень статической неопределимости балки:

.

Основная и эквивалентная система приведены на рис.36,б,в. Так выбор основной системы является наиболее рациональным, но не единственным. Можно было, например, заменить жесткую заделку на шарнирнонеподвижную опору; тогда основная система представляла бы собой статически определимую шарнирную балку, а лишняя неизвестная – сосредоточенный момент X, приложенный к левой опоре.

Эпюра изгибающих моментов от внешней нагрузки 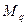(рис.36,д) имеет размерность Кн·м, а единичная эпюра моментов (рис.36,ж) - м.

Каноническое уравнение метода сил:

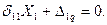
Вычисляем коэффициенты и , перемножая соответствующие эпюры по правилу Верещагина:

Реакция лишней связи:

Таким образом, исходная статически неопределимая система, загруженная распределенной нагрузкой q, приведена к статически определимой системе (жестко защемленная балка), загруженной распределенной нагрузкой q и сосредоточенной силой 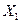(рис.36, з).

На рис.37,а,б представлены эпюры поперечных сил Qи изгибающих моментов 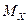для заданной системы.

Отметим, что эпюры Qи 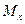(рис.37) построены непосредственно методом сечений, причем по условиям задачи построение эпюры Qне является обязательным. Тем не менее эта эпюра позволила определить сечение, в котором будет экстремум на эпюре .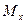

Рис. 37

Использование формулы (3.8) в виде:

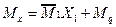(3.8)

не дает ответа на вопрос о месте нахождения экстремума и делает правильное построение эпюры 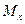более сложной задачей, требующей определенных навыков.

Пример 19. Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.38,а).

Степень статической неопределимости рамы:

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.38,б), т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.38,в).

Заменяя реакцию лишней связи соответствующей единичной силой,

(рис. 38,г) строим эпюру моментов (рис.38,д).

Грузовая эпюра моментов 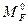(рис.38,ж), построенная от одновременного действия всех внешних нагрузок (рис.38,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой 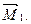В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра 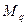) и от совместного действия F и M (эпюра 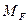). Эти варианты нагружения и эпюры представлены на рис.38,з и рис.39,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

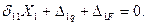
Вычислим коэффициенты канонического уравнения:

Реакция лишних связи:

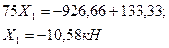
Эпюры N_z, Q_y, M_x для заданной системы, загруженной нагрузками F, M, q и X₁ (рис.39,г) представлены на рис.39,д,е,ж.

Как уже говорилось в гл.1, при построении эпюр 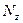и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр 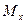знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В обоих рассмотренных примерах универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как балка (пример 18) и рама (пример 19) имеют степень статической неопределимости 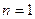, а, значит, суммарная единичная эпюра 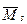(если ее построить) совпадет с единичной эпюрой . В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов .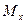

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.38,а). Должно выполняться условие:

Покажем отдельно фрагменты перемножаемых эпюр (рис.38,д и рис.39,ж) для ригеля (рис.40,а,б) и стойки (рис.40,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.40,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры 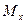с осью (рис.40,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент 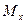определяется в виде:

Пересечение с осью означает, что в этом сечении 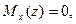поэтому подставляя числовые значения, для определения z при 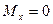получим квадратное уравнение:

откуда (второй корень этого уравнения лишен физического смысла).

 

Рис. 38

Рис. 39

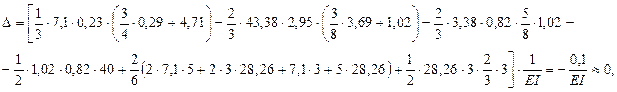
следовательно, расчет выполнен правильно.

Перейдем к рассмотрению более сложной системы – рамы с двумя лишними связями, для которой алгоритм расчета, приведенный в параграфе 3.3, можно реализовать в полном объеме.

Рис. 40

Пример 20. Для рамы (рис.41,а) построить эпюры Выполнить промежуточные и окончательные проверки в соответствии с алгоритмом расчета, указанным в параграфе 3.3.

Заданная рама имеет в опорных закреплениях пять связей: две в опоре 1 и три в опоре 2, следовательно, система дважды статически неопределима:

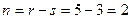
Основную систему целесообразно выбрать путем удаления шарнирной опоры (рис.41,б). Соответствующая эквивалентная система изображена на рис.41,в.

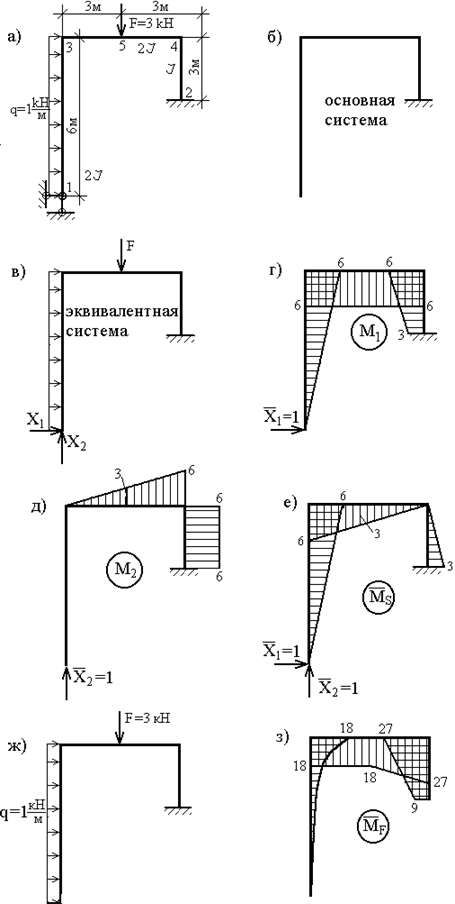
Рис. 41

Система канонических уравнений:

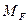Для вычисления коэффициентов и свободных членов канонических уравнений строим единичные рис.41,г,д) и грузовую (, рис.41, ж,з) эпюры изгибающих моментов, а для выполнения проверок – суммарную единичную эпюру 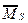(рис.41,е).

Коэффициенты системы канонических уравнений вычисляем путем перемножения соответствующих эпюр по правилу Верещагина. При этом обязательно учитываем разную жесткость элементов рамы (E2I – на левой стойке ригеля; EI – на правой стойке).

Для проверки вычисленных коэффициентов при неизвестных и свободных членов канонических уравнений используем суммарную единичную эпюру 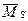(рис. 41,е).

 

 

Должны выполняться два условия:

1)

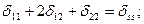
2)

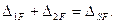
Вычисляем величины 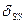и .

1)

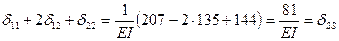
2)

таким образом, коэффициенты при неизвестных и свободные члены канонических уравнений вычислены правильно.

Вычисляем реакции лишних связей:

Строим эпюры продольных (N_z) и поперечных (Q_y) сил и изгибающих моментов (М_х) для заданной системы с учетом вычисленных реакций лишних связей (рис.43,а-г).

Для выполнения статической проверки необходимо вырезать жесткие узлы рамы 3 и 4 (рис.43,а) и убедиться в справедливости условий равновесия для каждого из них.

 

 

Условия равновесия для узла 3 (рис.42,а):

Условия равновесия для узла 4 (рис.42,б):

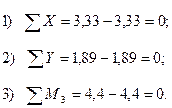
Таким образом, статическая проверка выполняется.

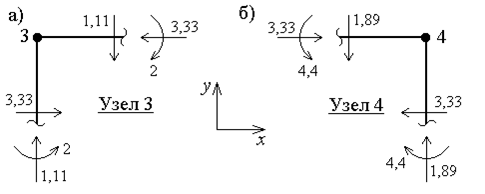
Рис. 42

Для выполнения кинематической проверки перемножим суммарную единичную эпюру 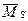(рис.41,е) и окончательную эпюру изгибающих моментов М_х (рис.43,г):

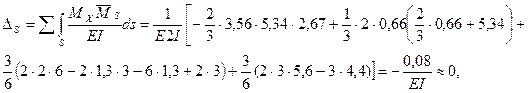
следовательно, все проверки метода сил выполняются, и расчет проделан правильно.

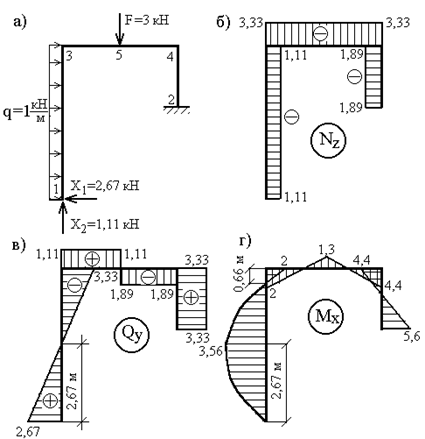
Рис. 43

Теперь рассмотрим примеры, иллюстрирующие различные способы использования симметрии.

Пример 21. Построить эпюры N_z, Q_y и M_x для симметричной рамы, загруженной несимметричной внешней нагрузкой (рис.44,а).

Заданная рама имеет два замкнутых бесшарнирных контура, следовательно, ее степень статической неопределимости

Записанная формально, без использования симметрии, система канонических уравнений метода сил имеет вид

Из многих возможных вариантов выбора основной системы наиболее целесообразным, максимально упрощающим расчет, является вариант, представленный на рис.44,б, полученный путем разрезания каждого из ригелей посредине пролета. Так как разрез стержня приводит к появлению трех неизвестных факторов (двух сил и момента), то эквивалентная система (рис.44,в) будет состоять из двух жестко защемленных рам, одна из которых загружена только неизвестными реакциями, а другая – такими же (по величине) реакциями и внешней нагрузкой.

Указанный выбор основной системы позволяет не только получить простые единичные эпюры (рис.44,г-и), но, что особенно важно, при этом целый ряд побочных коэффициентов системы канонических уравнений обращается в ноль. Это те коэффициенты, которые получаются путем перемножения симметричной и кососимметричной эпюр:

В силу теоремы о взаимности перемещений число нулевых коэффициентов удваивается. В результате формально записанная система канонических уравнений распадается на две самостоятельных системы:

I)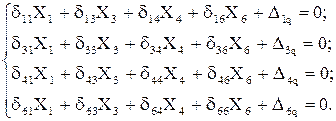

II)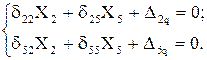

Вычисление коэффициентов этих систем уравнений (с обязательным учетом соотношения жестокостей элементов) приводит к следующим результатам:

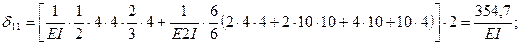
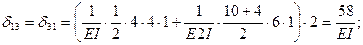
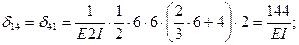
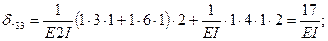
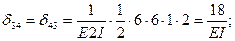
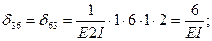
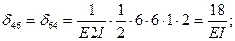
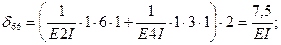
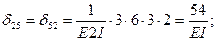
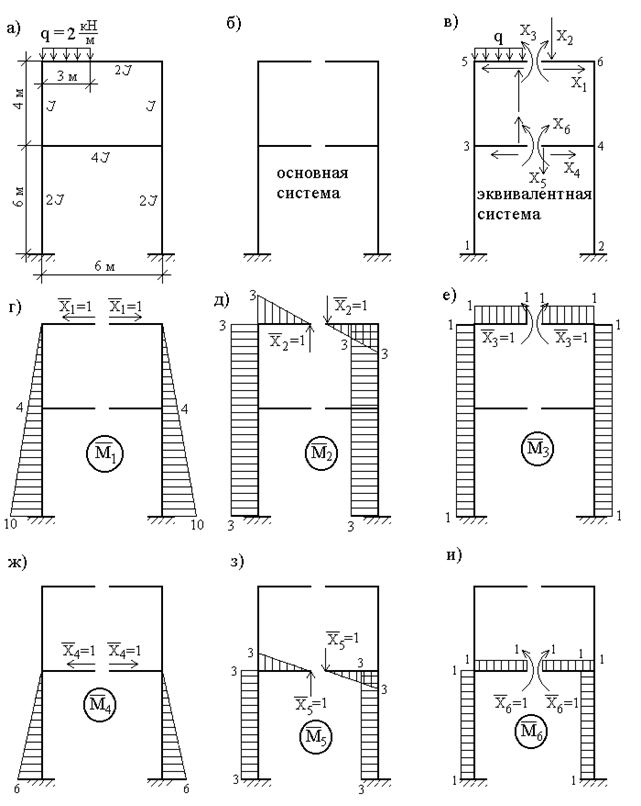
Рис. 44

 

Для выполнения проверки вычисленных перемещений строим суммарную единичную эпюру 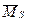от одновременного действия шести единичных факторов (рис.45,б).

Вычисляем коэффициенты 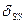и :

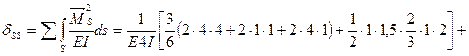
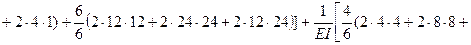
Выполняем проверку:

следовательно, коэффициенты и свободные члены систем канонических уравнений вычислены правильно.

Рис. 45

Подставляя вычисленные значения перемещений, получим системы канонических уравнений I и II в виде:

I.

II.

 

Решение системы I и II дает значения реакций лишних связей:

Окончательные эпюры N_z, Q_y, M_x, построенные от одновременного действия вычисленных реакций и внешней нагрузки q (рис.45,в) показаны на рис.45,г,д,е.

Пример 22. Построить эпюры N_z, Q_y, M_x в симметричной раме (рис.46.а).

Рама имеет два замкнутых бесшарнирных контура, поэтому она шесть раз статически неопределима. При обычном подходе в этом случае было бы необходимо решить систему шести линейных уравнений, т.е. расчет был бы весьма трудоемким. Использование симметрии, как это будет показано ниже, позволит свести задачу к решению только лишь двух линейных уравнений.

Выберем основную систему, разрезая каждый из ригелей посредине пролета (рис.46,б). Но, в отличие от предыдущего примера, сформируем две эквивалентных системы, одну из которых загрузим симметричными составляющими внешней нагрузки (рис.46,в), а другую – обратно симметричными составляющими (рис.46,г). Легко убедиться в том, что сумма внешних нагрузок, приложенных к обеим эквивалентным системам, равна внешней нагрузке, приложенной к заданной раме.

При действии симметричных самоуравновешенных сил и 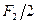(рис.46,в), приложенных в узлах, в элементах рамы отсутствуют изгибающие моменты и поперечные силы, а продольные силы возникают только в ригелях и вычисляются непосредственно из условий равновесия узлов 3 и 5, или, что то же самое, 4 и 6:

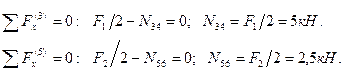
При действии обратносимметричных сил и 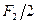(рис.46,г) в разрезах, сделанных по оси симметрии рамы, возникают обратносимметричные неизвестные поперечные силы Х₁, Х₂, а продольные силы и изгибающие моменты обращаются в ноль как симметричные усилия при обратносимметричной нагрузке.

Таким образом, для расчета рамы нужно составить только два канонических уравнения метода сил:

Единичные и грузовая эпюра изгибающих моментов показаны на рис.46,д,е,ж. Вычислим коэффициенты канонических уравнений путем перемножения соответствующих эпюр по правилу Верещагина:

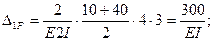
Единичные и грузовая эпюра изгибающих моментов показаны на рис.46,д,е,ж.

Рис. 45

Вычислим коэффициенты канонических уравнений путем перемножения соответствующих эпюр по правилу Верещагина:

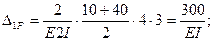
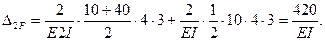
Для проверки вычисленных перемещений используем суммарную единичную эпюру изгибающих моментов 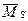(рис.46,з).

Проверка:

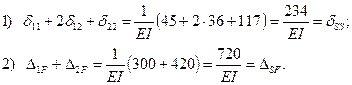
После подстановки найденных значений коэффициентов при неизвестных и свободных членов в канонические уравнения и умножения последних на EI получим:

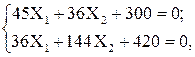
отсюда:

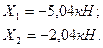
Таким образом, в результате раскрытия статической неопределимости исходная, шесть раз статически неопределимая система приведена к статически определимой системе (рис.46,и), загруженной внешней нагрузкой F₁ и F₂, продольными усилиями N₃₄ и N₅₆, а также вычисленными реакциями X₁ и X₂.

Эпюры продольных, поперечных сил и изгибающих моментов для заданной рамы показаны на рис.46,к,л,м.

Для выполнения универсальной кинематической проверки эпюры М_х используем суммарную единичную эпюру :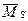

следовательно, задача решена правильно.

Пример 23. Построить эпюру изгибающих моментов для статически неопределимой рамы (рис.47,а), используя способ введения жестких консолей.

Этот способ используется для ортогонализации эпюр (т.е. для получения нулевых перемещений – коэффициентов канонических уравнений) в пределах каждого замкнутого или открытого с защемленными концами симметричного контура. Для ортогонализации эпюр с помощью жестких консолей соответствующие неизвестных переносятся в некоторую точку, называемую упругим центром. Положение этой точки определяется как положение центра тяжести условного тонкостенного сечения с толщиной

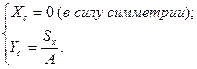
Заданная рама имеет степень статической неопределенности:

Для выбора основной системы (рис.47,б) используем то обстоятельство, что левый (П-образный) контур рамы симметричен. Разрежем его по оси симметрии, что будет эквивалентно удалению трех связей и появлению трех неизвестных реакций. Четвертую связь устраним путем удаления шарнирно-подвижной опоры. Введение в месте разреза жестких консолей с приложенными на их концах реакциями Х₁, Х₂, Х₃ совместно с реакцией Х₄ и внешними нагрузками приводит к эквивалентной системе (рис.47,в).

Определим положение упругого центра, т.е. фактически длину жестких консолей (рис.47,г), вычисляя координаты центра тяжести условного тонкостенного П-образного сечения:

Х_с=0;

Единичные эпюры изгибающих моментов показаны на рис.47,д,е,ж,з, а эпюра моментов от внешних нагрузок – на рис.47,и.

Учитывая, что результат перемножения симметричной эпюры на кососимметричную равен нулю, систему канонических уравнений метода сил рассматриваемой рамы запишем в виде:

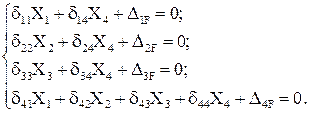
Вычислим коэффициенты уравнений, используя, как обычно, способ Верещагина:

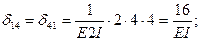
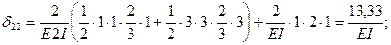
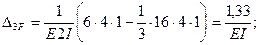
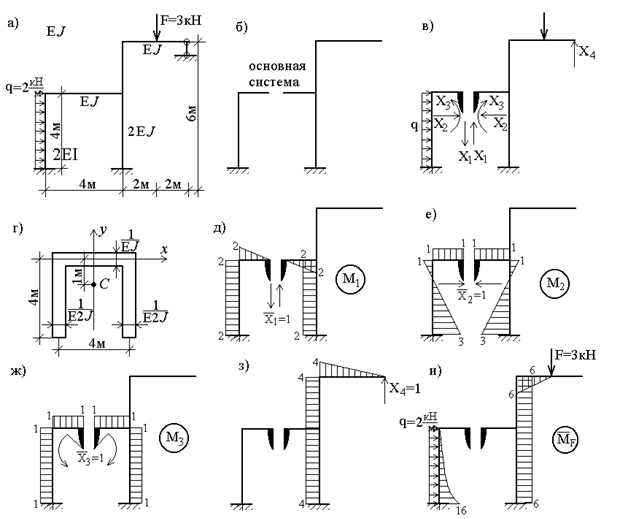
Рис. 47

 

Для проверки правильности вычисления коэффициентов и свободных членов канонических уравнений построим суммарную единичную эпюру изгибающих моментов 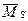(рис.48,а) и определим коэффициенты 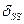и .

Рис. 48

Проверка:

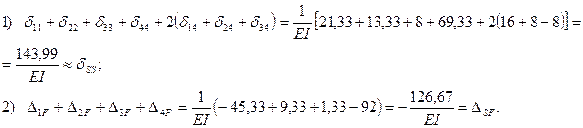
Следовательно, коэффициенты и свободные члены канонических уравнений вычислены правильно. Решение системы канонических уравнений дает следующие значения неизвестных:

Окончательная эпюра моментов для заданной рамы показана на рис.48,б.

Читатель имеет возможность самостоятельно убедиться в правильности построенной эпюры, перемножив ее с суммарной единичной эпюрой (результат, как известно, должен равняться нулю).

Глава 4 Построение эпюр в статически неопределимых системах. Метод перемещений

Сущность метода

Если в методе сил в качестве таких основных неизвестных выбираются внутренние усилия в фиксированных сечениях конструкции, то в методе перемещений… Для иллюстрации сказанного рассмотрим абсолютно жесткий брус, поддерживаемый…

Вспомогательная таблица метода перемещений

Как было показано в предыдущем параграфе, при расчете методом перемещений исходная система путем введения дополнительных связей расчленяется на ряд однопролетных статически неопределимых балок. Очевидно, что характер нагружения таких балок и способы закрепления их концов дают определенный, постоянный "набор" возможных вариантов, к определенной совокупности которых приводит расчетная схема любой заданной системы. Поэтому целесообразно заранее рассчитать однопролетные статически неопределимые балки при разных нагрузках и использовать эти результаты по мере необходимости. Обычно такой "набор" возможных вариантов представляется в табличной форме.

Рассмотрим несколько примеров, иллюстрирующих результаты, указанных в тех или иных строках приведенной таблицы.

1. Загружение сосредоточенной силой F однопролетной балки с жестким защемлением на одном конце и шарнирно подвижным опиранием на другом (строка 1 вспомогательной таблицы).

Для решения задачи используем метод сил. Эквивалентная система, единичная и грузовая эпюры для заданной схемы (рис.51,а) представлены на рис.51,б,в,г.

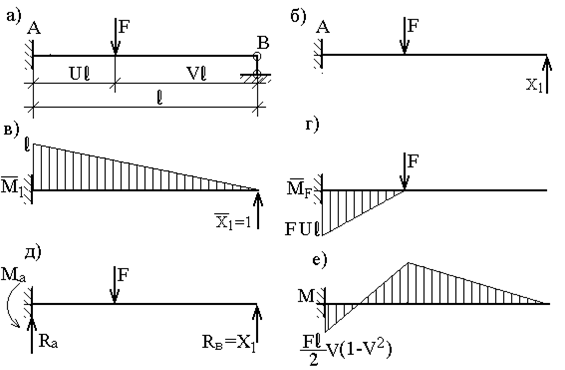
Рис. 51

Каноническое уравнение метода сил:

Коэффициенты канонических уравнений вычислим по способу Верещагина:

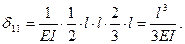
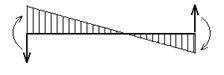
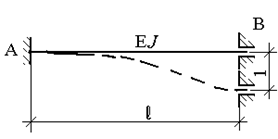
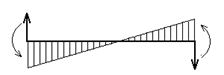
Вспомогательная таблица метода перемещений.

№	Схема балки и воздействия на нее	Эпюра моментов и реакции
		;
		; ;
		;
		;
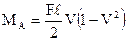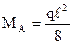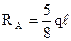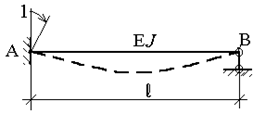
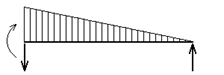
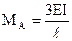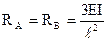
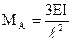
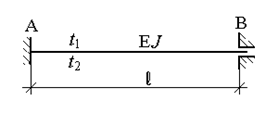
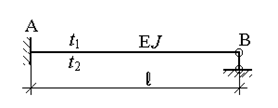
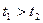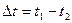
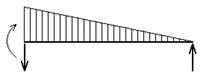
	Неравномерный нагрев	h – высота сечения

 

 

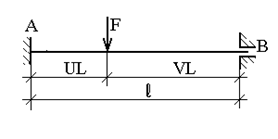
№	Схема балки и воздействия на нее	Эпюра моментов и реакции
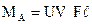
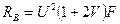
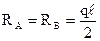
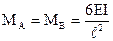
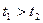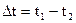
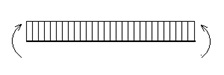
	Неравномерный нагрев	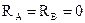h – высота сечения

 

 

Отметим, что при указанных условиях закрепления концов балки коэффициент не зависит от характера внешнего воздействия.

Так как и, следовательно, то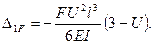

Подставляя и 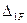в каноническое уравнение, находим:

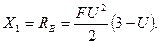
Тогда реакции левой опоры и опорный момент будут:

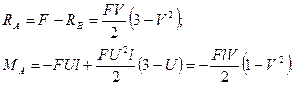
Окончательная эпюра моментов для заданной, теперь уже статически определимой, системы, загруженной силами F и X₁ (рис.51,д), показана на рис.51,е.

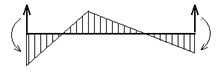
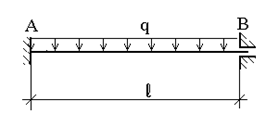
2. Загружение равномерно распределенной нагрузкой q (рис.52,а) однопролетной статически неопределимой балки (строка 2 вспомогательной таблицы).

Для решения вновь используем метод сил. Эпюра моментов от внешней нагрузки, приложенной к основной системе, показана на рис.52,б, а единичная эпюра моментов (и, соответственно, перемещение ) совпадает с построенной в предыдущем примере (рис.51,в).

Уравнение метода сил:

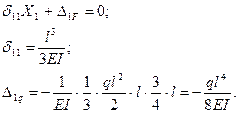
Рис. 52

Здесь при вычислении использованы эпюры 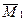(рис.51,в) и 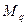(рис.52,б).

Реакция лишней связи:

X₁

Реакция левой опоры:

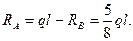
Опорный момент в левой опоре получим, просуммировав момент в этом сечении от нагрузки q с моментом от X₁:

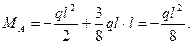
Направление опорных реакций и момента в заделке показаны на рис.52,в, а окончательная эпюра моментов – на рис.52,г.

3. Перемещение заделки на величину D по направлению перпендикулярному оси стержня (рис.53,а).

Эпюра изгибающих моментов в основной системе от смещения D будет нулевой, поэтому нулевым будет свободный член уравнения метода сил.

 

А перемещение по направлению Х₁ (рис.53,б) будет:

D_1D=D,

и уравнение метода сил принимает вид:

где 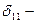то же, что и ранее.

Отсюда последовательно находим реакции 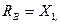и опорный момент :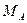

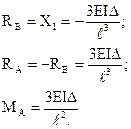
Направление этих величин показаны на рис.53,в, а окончательная эпюра моментов на рис.53,г.

При единичном смещении D=1 все вычисленные величины принимают значения, указанные в строке 4 вспомогательной таблицы метода перемещений.

Аналогичным образом можно рассчитать однопролетную балку на другие виды воздействий. Предоставив читателю возможность самостоятельно проделать соответствующие расчеты, отметим только, что при рассмотрении балки с двумя защемленными концами (строки 6 – 10 вспомогательной таблицы метода перемещений) целесообразно выбирать основную систему, разрезая балку посредине пролета. Такой разрез, как известно, приводит к появлению трех лишних неизвестных в методе сил – продольной и поперечной сил, а также изгибающего момента. Однако при всех рассматриваемых видах воздействий (вертикальные нагрузки, линейные смещения заделок по нормали к оси балки, поворот заделок) продольная сила будет равна нулю, поэтому решение всех задач приводит к системе двух канонических уравнений метода сил.

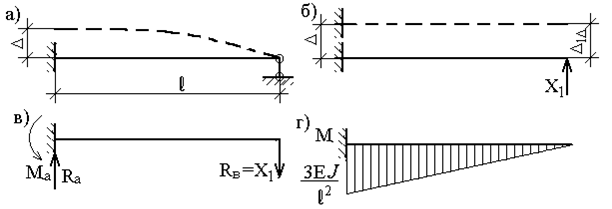
Рис. 53

Каноническое уравнение метода перемещений

(4.4) Заменим реактивный момент R1 суммой:

Алгоритм расчета систем методом перемещений

1. Находим степень кинематической неопределимости заданной системы. 2. Выбираем основную систему. 3. Записываем канонические уравнения метода перемещений.

Методы вычисления коэффициентов и свободных членов канонических уравнений

При статическом способе реактивные усилия во введенных связях определяют из уравнений равновесия отдельных узлов рамы или ее отсеченной части. Коэффициенты и свободные члены, представляющие собой реактивные моменты во… (4.8)

Проверки метода перемещений

Основной проверкой в методе перемещений является проверка равновесия узлов и других частей рамы. Количество проверяемых условий равновесия должно… Проверка правильности вычисления коэффициентов при неизвестных системы… Умножая эту эпюру последовательно на каждую из единичных эпюр, получим сумму коэффициентов при неизвестных в…

Использование симметрии при расчете рам методом перемещений

Расчет еще более упрощается, если разложить внешнюю нагрузку на симметричную и обратносимметричную. Другой подход состоит в том, что иногда в симметричных конструкциях вместо…

Примеры расчетов

Пример 24. Для рамы (рис.55,а) построить эпюру изгибающих моментов и выполнить все необходимые проверки расчета при условии, что жесткости всех элементов рамы одинаковы и равны EI.

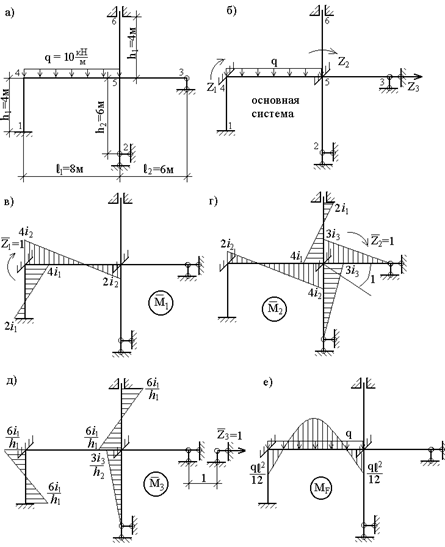
Рис. 55

Определим число основных неизвестных – степень кинематической неопределимости рамы. Так как число неизвестных угловых перемещений равно числу жестких узлов рамы, то n_y=2. Число независимых линейных смещений n_л=1. Действительно, узлы рамы 4 и 5 не могут перемещаться по вертикали из-за опорных закреплений 1 и 2 и принятой гипотезы о нерастяжимости стержней и неизменности их длинны при изгибе. Для них возможно только горизонтальное перемещение, которое будет одинаковым для узлов 4, 5 и 3 вследствие того, что они связаны между собой стержнями 4-5 и 5-3. Таким образом, степень кинематической неопределимости рамы:

Образуем основную систему, введя связи, препятствующие угловым и линейному смещениям, и обозначим предполагаемые направления (произвольно) трех неизвестных перемещений (рис.55,б). Используя приведенную выше вспомогательную таблицу метода перемещений, построим эпюры изгибающих моментов 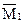, , от единичных перемещений введенных связей по заданным направлениям и эпюру 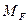от действия нагрузки на основную систему (рис.55,в-е). Для удобства на этих рисунках использованы следующие обозначения:

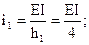
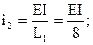
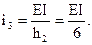
При построении всех указанных эпюр нужно четко представлять себе перемещение оси каждого стержня, вызванное заданным единичным смещением; это позволит установить положение сжатых волокон элементов рамы и правильно изобразить эпюры моментов.

Система канонических уравнений имеет вид:

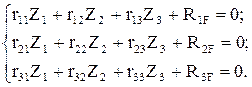
Для определения коэффициентов и свободных членов этих уравнений, которые представляют собой реактивные усилия в наложенных связях, применим статический способ. Для этого вырежем сначала узел 4 и рассмотрим условия его равновесия в случаях, представленных на рис.55,в-е, т.е. определим коэффициенты первой строки канонических уравнений.

На рис.56,а-г показан узел 4 с действующими на него моментами со стороны отброшенных частей рамы и реактивными моментами в защемлении (первой связи). Из условий равновесия этого узла получим:

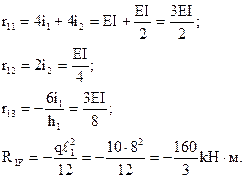
Отрицательный знак в двух последних случаях объясняется тем, что направления реактивных моментов 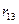и 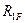противоположны заданному направлению угла поворота Z₁ первой связи.

Аналогично определим коэффициенты второго канонического уравнения. Для этого вырежем из рамы узел 5 и рассмотрим условия его равновесия при тех же четырех воздействиях на основную систему (рис.55,в-е).

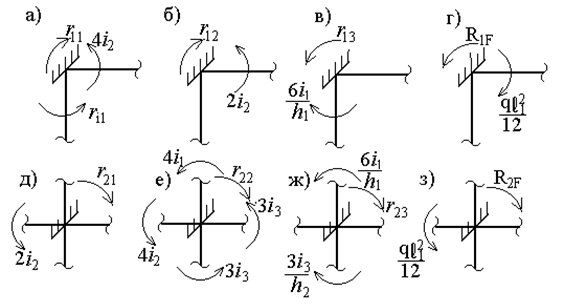
Рис. 56

 

Из рис.56,д-з следует:

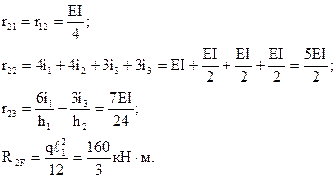
Для определения коэффициентов третьего уравнения, представляющих собой реакции во введенном стержне (третьей связи), рассечем стойки рамы и рассмотрим условия равновесия ее средней части, содержащей введенный стержень (рис.57,а-г). При этом под условием равновесия будем понимать равенство нулю суммы проекций всех сил, приложенных к выделенной части рамы, на горизонтальную ось: 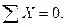Отличные от нуля проекции дадут искомые реакции во введенном стержне и поперечные силы, приложенные в местах рассечения стоек и определяемые по эпюрам 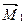, , 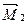, 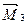M_F.

Рис. 57

 

Из рис.57,а-г следует:

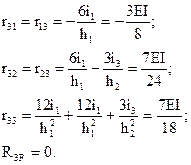
Проверку вычисленных коэффициентов и свободных членов можно осуществить способом перемножения эпюр. Для выполнения универсальной проверки построим суммарную единичную эпюру изгибающих моментов 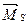, представляющую собой сумму единичных эпюр 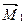, , 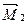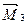(рис.58,а) и перемножим ее саму на себя:

Сумма коэффициентов при неизвестных составляет:

т.е.

коэффициенты вычислены правильно.

Для проверки свободных членов канонических уравнений необходимо построить эпюру изгибающих моментов 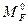от внешней нагрузки, приложенной в любой статически определимой системе, образованной из заданной рамы, и перемножить ее с эпюрой :

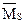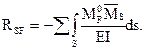
Два возможных варианта эпюры 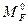представлены на рис.58,б,в (возможны и другие варианты статически определимых рам, образованных из заданной, и, соответственно, другие варианты эпюры 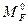). Легко убедиться, что результат перемножения любой из этих эпюр на эпюру 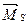равен нулю, что также подтверждает правильность вычислений, так как в рассматриваемом примере

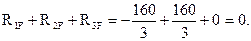
Подставляя найденные значения коэффициентов и свободных членов в исходную систему канонических уравнений, получим:

(4.17)

Решение системы (4.17) дает следующие значения неизвестных:

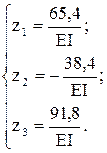
Единичные эпюры моментов (рис.55,в-д) теперь можно "исправить", т.е. умножить на соответствующие значения неизвестных. При этом вторая эпюра 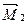поменяет знаки, так как z₂<0. Окончательную эпюру изгибающих моментов М (рис.58,г) построим согласно выражению:

(4.18)

 

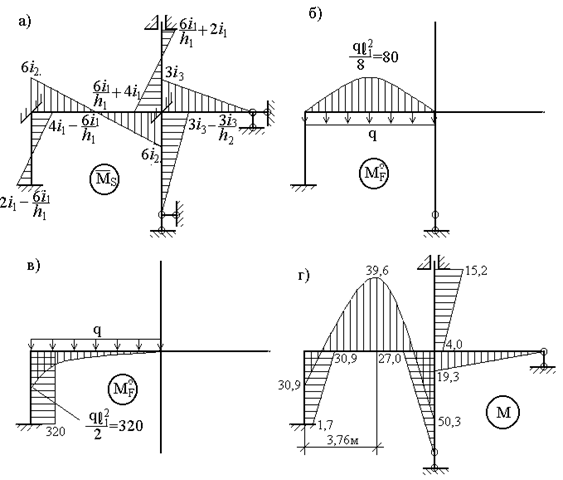
Рис. 58

Выполним статическую проверку. Для этого вырежем узлы 4 и 5, а также среднюю часть рамы (рис.59,а-в) и убедимся в выполнении условий равновесия.

Как уже говорилось, статическая проверка является достаточным критерием правильности выполненного расчета. Тем не менее, выполним дополнительно кинематическую проверку. Для этого построим суммарную единичную эпюру 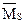в основной системе метода сил (рис.59,г). Читателю предоставляется возможность самостоятельно убедиться в том, что результат умножения этой эпюры на окончательную эпюру моментов М (рис.58,г) равен нулю.

В заключение отметим, что степень статической неопределимости рассмотренной рамы равна пяти, а это означает, что трудоемкость расчета данной системы методом сил значительно выше, чем при использовании метода перемещений.

 

Рис. 59

Пример 25. Для рамы с наклонными стойками (рис.60,а) построить эпюры M, Q, N при условии, что жесткость ригеля (2-3) в два раза больше чем жесткость наклонных стоек 1-2 и 3-4.

Определяем степень кинематической неопределимости рамы:

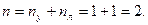
Основную систему образуем путем введения защемления в узле 2 и горизонтального опорного стержня в узле 3 (рис.60,б).

Для определения неизвестных перемещений z₁ и z₂ по направлениям введенных связей запишем систему канонических уравнений метода перемещений:

(4.19)

Используя вспомогательную таблицу метода перемещений, построим эпюры изгибающих моментов от единичного угла поворота 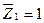и от внешней нагрузки (рис.60,в,г).

Отметим, что узловая нагрузка не вызывает изгибающих моментов в основной системе. Для построения эпюры моментов от единичного горизонтального перемещения 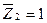второй связи необходимо знать, как перемещаются в этом случае концы стержней рамы. Перемещение узла 3 происходит по направлению, перпендикулярному линии 3-4 (искомое перемещение является горизонтальной проекцией полного смещения узла 3, а узла 2 – по направлению, перпендикулярному линии 1-2. В результате этого происходит относительное перемещение узлов 2 и 3 по вертикали.

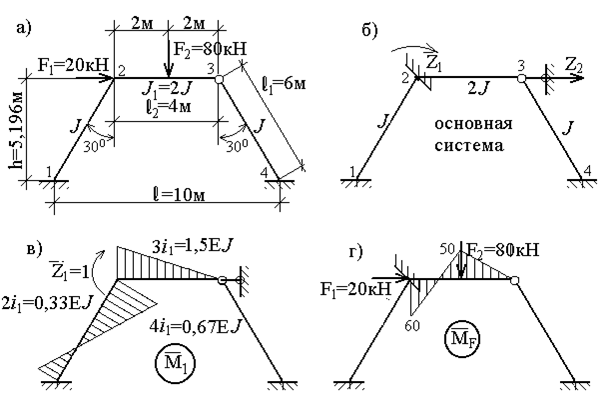
Рис. 60

Для определения указанных перемещений построим для шарнирной схемы, образованной из заданной рамы (рис.61,а),полярный план перемещений (рис.61,б). Из этого плана определим взаимное перемещение концов стержней:

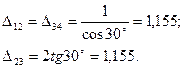
Так как введенное защемление препятствует повороту узла 2, то от найденных взаимных смещений произойдет изгиб стержней (рис.61,в). Эпюра моментов может быть теперь построена с помощью вспомогательной таблицы метода перемещений (рис.61,г).

Рис. 61

 

Коэффициенты r₁₁, r₁₂ и свободный член R_1F определим из условия равновесия узла 2:

Для определения коэффициента 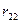, представляющего собой реакцию во введенном стержне от единичного смещения 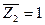, рассмотрим условия равновесия ригеля, отсеченного от стоек. Для этого необходимо определить поперечные и продольные силы, соответствующие эпюре , вырезав из рамы сначала узел 2, а затем узел 3. Так, условия равновесия узла 2 (рис.62,а) дают:

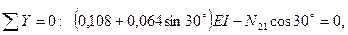
откуда

откуда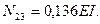

Условия равновесия узла 3 (рис.62,б) позволяют получить:

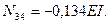
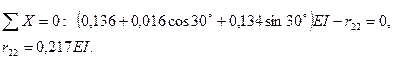
Аналогично можно определить и свободный член по эпюре 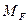, вырезая узлы 2 и 3 (рис.62,в,г):

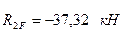
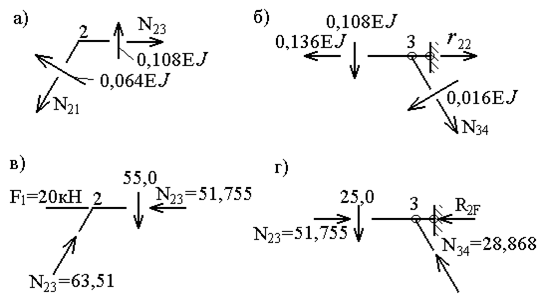
Рис. 62

Использование статического способа для вычисления коэффициентов и 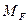для рамы с наклонными стойками приводит, как можно было убедиться из рассматриваемого примера, к усложнению расчетов. Поэтому в подобных случаях целесообразно использовать способ перемножения эпюр:

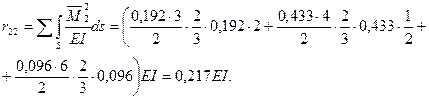
Для определения свободного члена способом перемножения эпюр нужно построить эпюру моментов от внешней нагрузки в статически определимой системе, образованной из заданной рамы (рис.63,а):

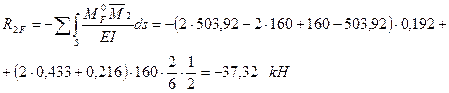
После подстановки вычисленных коэффициентов в уравнения (4.19) получим:

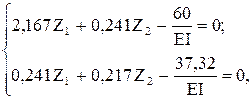
откуда:

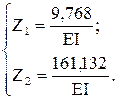
Окончательную эпюру моментов (рис.63,б) строим по формуле:

Соответствующие ей эпюры поперечных и продольных сил показаны на рис.63,в,г.

Рис. 63

Читателю предлагается самостоятельно убедиться в том, что для окончательных эпюр выполняются статические проверки: в узле 2 изгибающие моменты уравновешены; а силы, действующие на верхнюю отсеченную часть рамы, удовлетворяют условиям равновесия 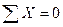и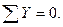

Пример 26. Используя упрощения, связанные с симметрией заданной рамы (рис.64,а), построить эпюру изгибающих моментов, при условии, что жесткости всех стержней одинаковы и равны EI.

Степень кинематической неопределимости рамы:

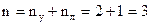
При выборе основной системы метода перемещений (рис.64,б) используем условия симметрии. Сгруппируем неизвестные углы поворота, т.е. угол поворота узла 2 представим в виде суммы двух углов поворота 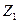и 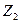, а поворот узла 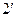, симметричного узлу 2, - в виде разности углов 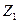и .

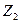Горизонтальное перемещение ригеля 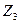является обратносимметричным неизвестным, так как узел 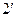при этом смещается от оси симетрии рамы, а симметричный ему узел 2 – к оси симметрии.

Для определения групповых неизвестных 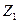, 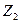и 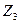запишем систему трех канонических уравнений метода перемещений:

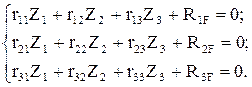(4.20)

Как видно, форма канонических уравнений при группировке неизвестных остается прежней. Но здесь все эпюры от единичных неизвестных (рис. 64, в-д) будут только симметричными или обратносимметричными, а канонические уравнения распадутся на две независимые системы, содержащие только симметричные или только обратносимметричные групповые неизвестные. При этом неизвестные перемещения узлов, расположенных на оси симметрии, всегда обладают симметрией или обратной симметрией и поэтому не группируются.

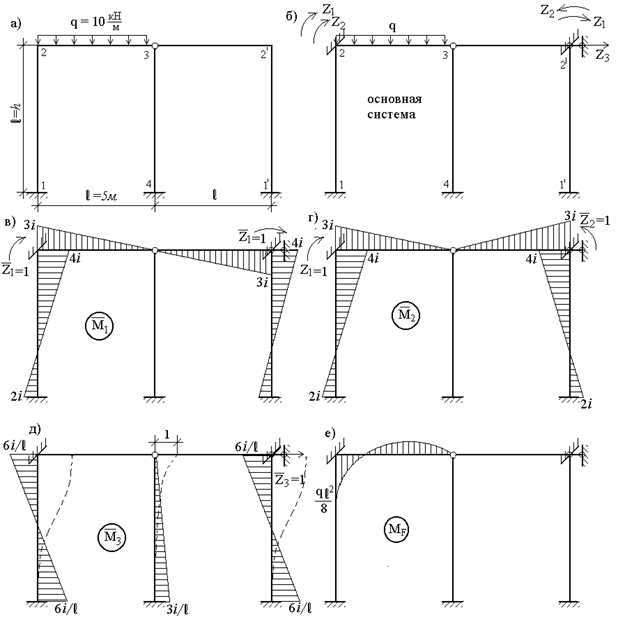
Рис. 64

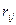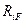Значения единичных коэффициентов и свободных членов в уравнениях (4.20) приобретают несколько иной смысл, чем ранее. Здесь и - обобщенные реакции, соответствующие обобщенному перемещению 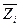от парного смещения и от внешней нагрузки. Эти обобщенные реакции определяются как алгебраические суммы простых реакций в связях, которые одновременно смещаются при групповом парном перемещении . Положительные направления простых реакций принимаются, как и ранее, совпадающими с задаваемыми направлениями перемещений тех связей, в которых они определяются.

При использовании статического способа для коэффициентов и свободных членов канонических уравнений (4.20) получим:

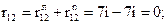
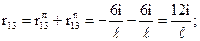
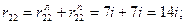
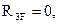
где индексами "л" и "n" обозначены соответственно левая (узел 2) и правая (узел 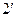) дополнительные заделки, в которых определяются обычные реакции (реактивные моменты). Реакции в дополнительном стержне (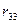и 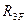) определены из условия равновесия 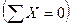отсеченного ригеля рамы.

Вследствие равенства нулю четырех коэффициентов система канонических уравнений (4.20) распадается на две системы, а точнее – на систему уравнений относительно неизвестных Z₁ и Z₃ и уравнение относительно Z₂:

В результате решения получим следующее значения неизвестных:

В этом примере обозначено:

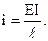
Окончательная эпюра моментов (рис.65) имеет вид:

Рис. 65

Литература:

1. Дарков А.В., Шапашников Н.Н. Строительная механика: Учеб. для строит. спец. вузов. – 8-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 607с.: ил.

2.Руководство к практическим занятиям по курсу строительной механики (статика стержневых систем): Учеб. особие для студентов вузов /Г.К. Клейн, Н.Н. Леонтьев, М. Г. Ванюшенков и др.; Под ред. Г.Г. Клейна. 4-е изд., перераб. и доп. – М.: Высшая школа /1980. – 384с.: ил.

3.Справочник по сопротивлению материалов /Писаренко Г.С., Яковлев А.П., Матвеев В.В.; Отв. ред. Писаренко Г.С. – 2-е изд., перераб. и доп. – Киев: Наук. думка, 1988. – 736с.: ил.

4.Строительная механика: Учебник для вузов /Ю.И. Бутейко, Н.А. Засядько, С.Н. Кан и др.; Под ред. Ю.И. Бутенко. – К.: Выща шк., 1989. – 479с.; ил.

5.Строительная механика. Стержневые системы: Учебник для вузов /А.Ф. Смирнов, А.В. Александров, Б.Я. Лащенков, Н.Н. Шапошников; Под ред. А.Ф. Смирнова. – М.: Стройиздат, 1981. – 512с; ил.