Множество действительных чисел

Лекция 1

Множества.

Множество действительных чисел.

Виды числовых множеств.

Окрестность точки.

 

Математический анализ функций одной переменной.

 

Множества.

В математике все понятия делятся на первичные (основные неопределяемые понятия) и определяемые через первичные или уже известные. Первичными…   Под множеством понимают совокупность некоторых элементов.

Операции над множествами.

Для визуализации отношений между множествами и операций над множествами обычно используются диаграммы Эйлера-Венна, на которых представлены результаты операций над множествами точек как над геометрическими фигурами на плоскости. Универсальное множество обычно обозначают графически в виде множества точек прямоугольника, а отдельные множества в виде отдельных областей (кругов или овалов) внутри этого прямоугольника.

 

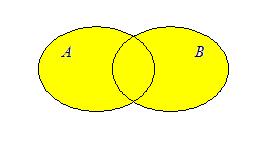
Определение 1: Объединением (или суммой) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств, то есть или А, или В:

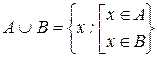
По аналогии с алгеброй чисел объединение иногда называют суммой множеств, так как операция объединения множеств обладает многими свойствами операции сложения чисел.

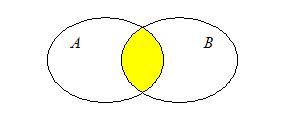
Определение 2: Пересечением (или произведением) двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит обоим этим множествам, то есть и А, и В:

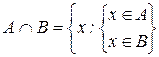
По аналогии с алгеброй чисел пересечение иногда называют произведением множеств, так как операция пересечения множеств обладает многими свойствами операции умножения чисел.

 

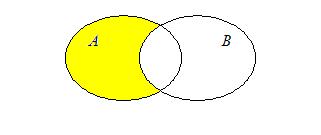
Определение 3: Разностью двух множеств А и В называется новое множество, состоящее из элементов, каждый из которых принадлежит множеству А, но не принадлежит множеству В:

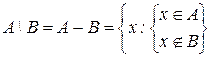
Множество АВ называется также дополнением множества В относительно множества А.

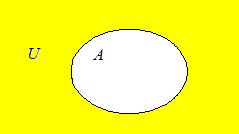
Определение 4: Если U – универсальное множество и АÌU, то разность UA называется дополнением множества А до множества U, или просто дополнением множества А и обозначается Ā:

 

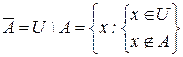
Определение 5: Симметрической разностью двух множеств А и В называется новое множество, обозначаемое АDВ и состоящее из тех и только из тех элементов, которые принадлежат АВ или ВА:

 

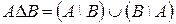
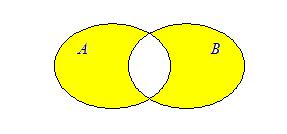
Пример:

Выписать все подмножества трёхэлементного множества М={а, b, c}.

М

{а, b, c}

 

{а, b} {а, c} {b, c}

 

{а } {b} { c}

 

Æ

 

Определение 6: Алгебра множеств — это непустая система подмножеств (некоторого множества U), замкнутая относительно операций объединения, пересечения, дополнения и симметрической разности.

Например, алгебра натуральных чисел незамкнута относительно вычитания.

 

В теории алгебры множеств множества Æ и U играют такую же роль, что и числа 0 и 1 в теории алгебры чисел.

 

Основные свойства алгебры множеств:

 

	Объединение È	Пересечение Ç	Разность	Симметрическая разность D
Коммутативность	АÈВ=ВÈА	АÇВ=ВÇА	¾	АDВ=ВDА
Ассоциативность	(АÈВ)ÈС=АÈ(ВÈС)	(АÇВ)ÇС=АÇ(ВÇС)	¾	(АDВ)DС=АD(ВDС)
Дистрибутивность	(АÇВ)ÈС=(АÇС)È(ВÇС)	(АÈВ)ÇС=(АÈС)Ç(ВÈС)	¾	¾
Дистрибутивность	(АВ)ÈС=(АС)È(ВС)	(АВ)ÇС=(АС)Ç(ВС)	¾	¾
	АÈА=	АÇА=	АА=	АDА=Æ
	АÈĀ=	АÇĀ=	АĀ=	АDĀ=
	ĀÈА=	ĀÇА=	ĀА=	ĀDА=
	АÈÆ=	АÇÆ=	АÆ=	АDÆ=А
	ÆÈА=	ÆÇА=	ÆА=	ÆDА=А
	АÈU=	АÇU=	АU=	АDU=
	UÈА=	UÇА=	UА=	UDА=
	UÈÆ=	UÇÆ=	UÆ=	UDÆ=
	ÆÈU=	ÆÇU=	ÆU=	ÆDU=
Законы де Моргана			¾	¾
				¾

 

Множество действительных чисел.

Множество вещественных чисел разбивается на два множества — Q рациональных и`Q (I) иррациональных чисел.   Определение 1: Рациональным называется число, которое можно представить в виде p/q, где р и q — целые числа, причем…

Основные свойства вещественных чисел.

I. Сложение и умножение вещественных чисел

Определение 3: Для любой пары а и b вещественных чисел определены, и притом единственным образом, два вещественных числа a+b и а·b, называемые их…   Каковы бы ни были числа a, b и с:

II. Сравнение вещественных чисел.

Отношение = обладает транзитивным свойством: если а=b и b=с, то а=с.    

III. Непрерывность вещественных чисел.

13) Пусть X и Y — два множества, состоящие из вещественных чисел. Тогда, если для любых чисел хÎХ и yÎY выполняется неравенство… х£с£у. Следует заметить, что свойством непрерывности обладает множество всех вещественных чисел, но им не обладает множество…

Виды числовых множеств. Окрестность точки.

  Конечные числовые промежутки 1. {x| a£x£b}=[a; b] замкнутый промежуток (интервал) …   Все эти множества называются промежутками (интервалами).

Простейшие логические символы

 

Лекция 2

Алгебраическая форма комплексного числа.

Геометрическое изображение комплексных чисел.

Тригонометрическая форма комплексного числа.

Показательная форма комплексного числа.

Основные действия над комплексными числами.

 

Комплексные числа.

 

Алгебраическая форма комплексного числа.

Определение 1:Комплексным числом z называется выражение z=а+ib, где а и b - действительные числа; i - так называемая мнимая единица,определяемая…   Определение 2Если а=0, то число 0+ib=ib называется чисто мнимым;если b=0, то получается действительное число:…

Определение 3Два комплексных числа z=а+ib и `z=а-ib, отличающихся только знаком мнимой части, называются сопряженными.

 

Определение 4Два комплексных числа z1=а1+ib1 и z2=а2+ib2, считаются равными z1=z2, если равны в отдельности их действительные и мнимые части, то есть а1=а2, b1=b2.

 

Определение 5Комплексное число z равно нулю тогда и только тогда, когда равны в отдельности нулю его действительная и мнимая части, то есть а=0, b=0.

 

 

Геометрическое изображение комплексных чисел.

Всякое комплексное число z=а+ib можно изобразить на плоскости Оху в виде точки А(а, b) с координатами а и b. Обратно, каждой точке плоскости М(х, у)…   Определение 1Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного z. …

Определение 2:На плоскости комплексного переменного z ось Оу называют мнимой осью, а ось Ох называют действительной осью.

Соединив точку А(а, b) с началом координат, получим вектор ОА, который принято считать геометрическим изображением комплексного числа z=а+ib.

 

Кроме записи z=а+ib употребляют z=х+iу.

Тригонометрическая форма комплексного числа.

  Определение 1:Выражение r(cosj+isinj), называется тригонометрической формой… z=r(cosj+isinj).

Основные действия над комплексными числами.

· Сложение комплексных чисел. Суммой двух комплексных чисел z1=а1+ib1 и z2=а2+ib2, называется комплексное число, определяемое равенством: z1+ z2=(а1+ib1)+(а2+ib2)=(а1+а2)+i(b1+b2).  

Произведение двух комплексных чисел есть такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

Замечание 1: Произведение сопряженных комплексных чисел z=а+ib и`z=а-ib есть действительное число и выражается так:

z`z = а²+b²

Произведение сопряженных комплексных чисел равняется квадрату модуля каждого из них.

· Деление комплексных чисел. Деление комплексных чисел определяется как действие, обратное умножению.

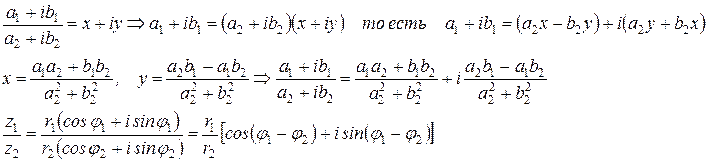
Таким образом, модуль частного двух комплексных чисел равен частному модулей делимого и делителя; аргумент частного равен разности аргументов делимого и делителя.

Замечание 2: Из правил действий над комплексными числами следует, что в результате операций сложения, вычитания, умножения и деления комплексных чисел получается снова комплексное число.

Если правила действий над комплексными числами применить к действительным числам, рассматривая их как частный случай комплексных, то эти правила будут совпадать с обычными правилами действий, известными из арифметики.

 

Замечание 3Вернувшись к определениям суммы, разности, произведения и частного комплексных чисел, легко проверить, что если в этих выражениях заменить каждое комплексное число сопряженным, то и результаты указанных действий заменяются сопряженными числами. Отсюда, в частности, вытекает следующая теорема:

Теорема :Если в многочлен с действительными коэффициентами

А₀хⁿ+А₁х^n-1+ ...+А_п

подставить вместо х число а+ib, а затем сопряженное число а-ib, то и результаты этих подстановок будут взаимно сопряженными.

Например: Выполнить действия над комплексными числами в алгебраической форме и тригонометрической форме и сопоставить результаты: z₁=-2+2i; z₂=1-i

Комплексные числа и действия над ними

 

Лекция 3

Возведение комплексного числа в степень.

Извлечение корня n-ой степени из комплексного числа.

Возведение в степень и извлечение корня.

· Возведение комплексного числа в степень Формула Муавра Если п — целое положительное число, то [r(cosj+isinj)]n=rn(cosnj+isinnj). при возведении комплексного числа (в тригонометрической форме) в целую положительную степень модуль возводится в эту…

Числа

 

b=0 a=0

 

 

Комплексные числа и действия над ними.

 

Лекция 4

Разложение многочлена на множители.

Виды многочленов.

Кратные корни многочлена.

Разложение многочлена на множители в случае комплексных корней.

 

 

Многочлены.

Разложение многочлена на множители.

  Определение 2: Корнем многочлена называется такое значение переменной х, при…  

Кратные корни многочлена.

Q(x)=A0(x-а1)(x-а2)…(x-аn) некоторые линейные множители окажутся одинаковыми, то их можно объединить, и… Q(x)=A0(x-а1)k1(x-а2) k2…(x-аm) km, где k1+k2+…+km=n и m£n.

Разложение многочлена на множители в случае комплексных корней.

Среди корней многочлена могут быть и комплексные. Теорема 1:Если a=а+ib корень многочлена (r-кратный) с вещественными… Перемножив два множителя (с сопряжёнными комплексными корнями) получаем:

Лекция 5

Разложение рациональной функции на элементарные дроби

Полярная система координат

Понятие функции

Способы задания функции

Классификация функций

 

Разложение рациональной функции на элементарные дроби.

Теорема 1:Если рациональная функция имеет степень многочлена в числителе меньше степени многочлена в знаменателе, а многочлен Q(x) представим в… Q(x)=А(x-a)r(x-b)s…(x2+px+q)t(x2+ux+v)l, то эту функцию можно представить единственным образом в виде:

Полярная система координат.

Определение 2: Полярными координатами точки М называются числа r и j. При этом число r - полярный радиус, число j - полярный угол. М(r; j), где… Установим связь между полярными координатами точки и ее прямоугольными… Пусть точка М имеет прямоугольные координаты х и у и полярные координаты r и j

Понятие функции.

Пусть X и Y—некоторые числовые множества. Определение 1: Функцией f называется множество упорядоченных пар чисел (х; у)…  

Заметим, что не всякая линия является графиком функции.

Определение 6: Функция называется явной, если она задана формулой y=f(x).

 

Определение 7: Функция называется неявной, если она задана уравнением F(x; у)=0.

Способы задания функции.

Существуют три основных способа задания функций: аналитический, табличный и графический.

1) Аналитический способ - зависимость между переменными величинами определяется с помощью формулы, указывающей, какие и в каком порядке действия нужно выполнить, чтобы получить значение функции, соответствующее данному значению аргумента.

 

2) Табличный способ - зависимость между переменными величинами определяется с помощью указанной таблицы. Область определения – множество чисел, расположенных в первой строке (столбце) таблицы, область значений – множество чисел, расположенных во второй строке (столбце) таблицы. Так задаются функции с конечными значениями.

 

3) Графический способ - зависимость между переменными задаётся посредством графика.

Определение 1: Если на некотором множестве X определена функция z=j(x) со множеством значений Z, а на множестве Z - функция y=f(z), то функция у=f[j(х)] называется сложной функцией от х (или суперпозицией функций j(x)и f(z)), а переменная z - промежуточной переменной сложной функции.

 

Определение 2: Пусть X и Y—некоторые мно­жества и пусть задана функция f, т. е. множество пар чисел (х; у) (хÎX, уÎY), в котором каждое число х входит в одну и только одну пару, а каждое число y - по крайней мере в одну пару. Если в каждой паре этого множества числа х и у поменять местами, то получим множество пар чисел (у; х), которое называется обратной функцией j к функции f.

Обратная функция в данном понимании может функцией и не являться.

 

Функция может быть задана параметрически на множестве Х посредством переменной t, называемой параметром:

 

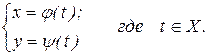
Классификация функций.

Определение 1: Простейшими элементарными функциями являются:

· постоянная функция f(х)=С, С=const,

· степенная функция f(х)=х^a (a—любое число),

· показательная функция f(х)=а^х (0<а¹1),

· лога­рифмическая функция f(х)=log_aх (0<а¹1),

· тригонометри­ческие функции f(х)=sinx, f(х)=cosx, f(х)=tgx, f(х)=ctgx,

· обратные тригонометрические функции f(х)=arcsinx, f(х)=arccosx, f(х)=arctgх, f(х)=arcctgx.

Определение 2: Все функции, получаемые с помощью конечного числа арифметических действий над простейшими элементарными функциями, а также суперпозицией этих функций, составляют класс элементарных функций.

 

На основании определения следует, что элементарные функции являются функции заданные аналитически.

 

Классификация элемен­тарных функций:

1) Функция вида Р(х)=a₀х^m+a₁х^m-1+…+a_m-1х+a_m, где m³0 - целое число, a₀, a₁, …, a_m-1, a_m любые числа — коэффициенты (а₀¹0), называется целой ра­циональной функцией или многочленом степени m. Многочлен первой степени называется также линейной функцией.

 

2) Функция, представляющая собой отношение двух целых рациональных функций

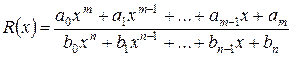, называется дробно-рациональной функцией.

 

Совокупность целых рациональных (1) и дробно-рацио­нальных (2) функций образует класс рациональных функций.

 

3) Функция, полученная с помощью конечного числа суперпозиций и четырех арифметических действий над степенными функциями как с целыми, так и с дробными показателями и не являющаяся рациональ­ной, называется иррациональной.

 

Алгебраические функции: рациональ­ные (1 и 2) и иррациональные (3).

 

4) Всякая функция, не являющаяся алгебраической, называется трансцендентной функцией.

 

 

Лекция 6

Числовая последовательность

Бесконечно малые и бесконечно большие последовательности

Предел числовой последовательности

 

Числовая последовательность.

  Определение 2: Последовательность {хn} называется ограниченной сверху (снизу),…  

Прогрессии

Бесконечно малые и бесконечно большие последовательности.

Определение 1: Последовательность {bn} называется бесконечно большой, если для любого положительного числа А существует номер N, такой, что при… Любая бесконечно большая последовательность является неограниченной. Однако…  

Предел числовой последовательности.

  Определение 2: Последовательность {хn} не являющаяся сходящейся называется…  

Лекция 7

Предел функции

Основные теоремы о пределах

Два замечательных предела

 

Предел функции.

Функция может иметь в точке только один предел.   Определение 2 (по Коши): Число А называется пределом функции f(х) в точке х=х0, если для любого числа e>0…

Основные теоремы о пределах.

Теорема 2: Сходящаяся последовательность ограничена. Замечание: Ограниченная последовательность может быть расходящейся.  

Два замечательных предела.

Первый замечательный предел (0/0):

 

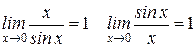
Второй замечательный предел (1^¥):

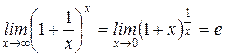
Лекция 8

Бесконечно малые и бесконечно большие функции

Эквивалентные бесконечно малые функции

Непрерывность функции в точке

 

 

Бесконечно малые и бесконечно большие функции.

Бесконечно малые функции обладают такими же свойствами, что и бесконечно малые последовательности.   Определение 2: Функция f(x) называется бесконечно большой функцией в точке х=х0 (или при х®х0), если .

Эквивалентные бесконечно малые функции.

при х®0:

 

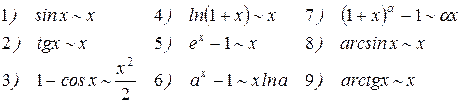
Непрерывность функции в точке.

Определение 1: Функция f(x) называется непрерывной в точке х0, если предел функции и её значение в этой точке равны, т. е. Определение 2: «на языке последовательностей» Функция f(x) называется непрерывной в точке х0, если для любой…

Лекция 9

Классификация точек разрыва

Непрерывность функции на промежутке

Производная функции

 

Классификация точек разрыва

Определение 1: Точка х₀ называется точкой разрыва функции f(x), если f(x) в точке х₀ не является непрерывной.

Разрывы функций классифицируются следующим образом.

 

Разрыв первого рода.

Определение 2: Точка х₀ называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные правый и левый пределы и

а) если правый и левый пределы равны друг другу, но не равны значению функции f(x) в этой точке, то х₀ называется точкой устранимого разрыва и имеет место скачок функции.

б) если правый и левый пределы не равны друг другу, то х₀ называется точкой конечного разрыва.

 

Разрыв второго рода.

Определение 3: Точка х₀ называется точкой разрыва второго рода функции f(x), если в этой точке функция f(x) не имеет по крайней мере одного из односторонних пределов, или хотя бы один из односторонних пределов бесконечен.

 

Непрерывность функции на промежутке.

Определение 1: Функция f(x) называется непрерывной в интервале (а; b), если она непрерывна в каждой точке этого интервала. Определение 2: Функция f(x) называется непрерывной на отрезке [а; b], если она непрерывна в каждой точке интервала (а;…

Всякая элементарная функция непрерывна на своей области определения.

Теорема 1: (об устойчивости знака непрерывной функции) Пусть функция f(х) непрерывна в точке х0 и f(х0)¹0. Тогда существует d>0 такое, что…   Теорема 2: (I теорема Больцано-Коши) Пусть функция f(х) непрерывна на отрезке [а; b] и на концах отрезка имеет…

Производная функции.

  Определение 1: Производной функции у=f(x) в точке х0 называется предел при…

Дифференцирование сложной функции.

Теорема: Если функция х=j(t) имеет производную в точке t0, а функция y=f(x) имеет производную в соответствующей точке х0=j(t0), то сложная функция… Основные правила нахождения производных. Производная суммы…

Лекция 10

Понятие дифференциала

Производные высших порядков

Дифференциалы высших порядков

Дифференцирование функции заданной параметрически

 

Понятие дифференциала.

Dу=АDх+a(Dх)Dх, где . Первое слагаемое: АDх является при Dх®0 бесконечно малой одного порядка с Dх,… .

Производные высших порядков.

  Определение 1: Назовем f¢(х) производной первого порядка.  

Дифференциалы высших порядков.

Определение 1: Пусть функция f(х) дифференцируема в каждой точке х некоторого промежутка, тогда её дифференциал dy=f¢(х)dх, назовём…   Итак, dy является функцией двух переменных: аргумента х и его дифференциала dx.

Дифференцирование функции заданной параметрически.

Пусть функция задана параметрически на множестве Х посредством переменной t, называемой параметром:  

Логарифмическое дифференцирование.

 

При дифференцировании выражений, имеющих вид, удобный для логарифмирования, можно предварительно выполнить логарифмирование.

Замечание: Если в качестве переменной дифференцирования выступает у (переменная, которая является не аргументом, а функцией), необходимо вычислять производную согласно рассмотренным правилам, обязательно умножая на у¢ (на производную внутренней функции).

 

Продифференцировать функцию: .

Логарифмируя по основанию е находим: Применим основное свойство логарифма: Дифференцируем обе части равенства:

Продифференцировать функцию: .

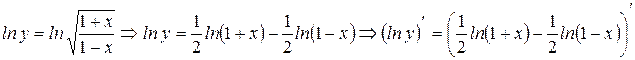
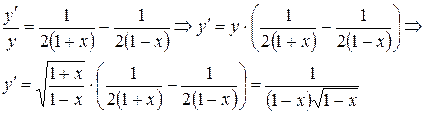
Продифференцировать функцию: .

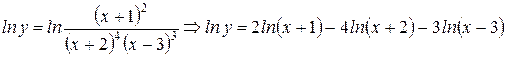
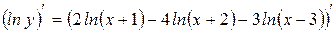
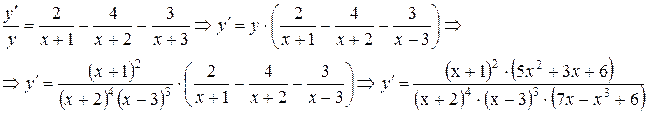
Дифференцирование неявной функции.

Пусть уравнение, связывающее х и у, определяет у, как неявную функцию х. Для нахождения производной , в точке х=х0, у=у0 не нужно искать явное… Замечание: Если в качестве переменной дифференцирования выступает у… Найти первую и вторую производные неявной функции:

.

Дифференцируя обе части уравнения получаем: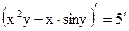

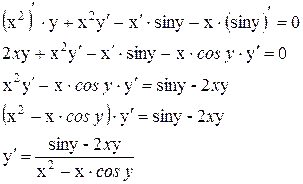
Для вычисления второй производной, дифференцируем обе части уравнения, получаем: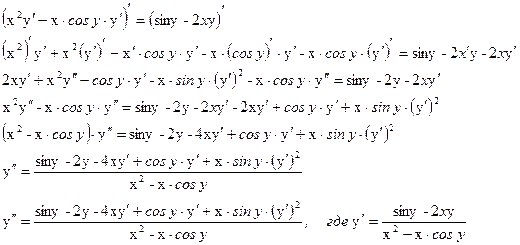

Лекция 11

 

Основные теоремы дифференциального исчисления.

  Геометрический смысл: если в точке х0 дифференцируемая функция f(x) имеет… Теорема не верна если функцию f(x) рассматривать на отрезке [а, b].

Правило Лопиталя.

Замечание 1: Правило Лопиталя раскрывает неопределённости типа и . Замечание 2: Правило Лопиталя может применяться многократно

Возрастание (убывание) функции. Экстремумы.

  Теорема 2 (признак возрастания (убывания): Если функция f(х) дифференцируема…  

Выпуклость (вогнутость) функции. Перегибы.

Определение 1: Будем говорить, что график функции у=f(x) имеет на (a, b)… Замечание: на участке выпуклости касательные к графику функции не пересекаются с самим графиком и имеют с ним лишь…

Асимптоты.

Существует три вида асимптот: вертикальные, горизонтальные и наклонные. Определение 2: Прямая х=х0 называется вертикальной асимптотой графика функции… Определение 3: Прямая у=а называется горизонтальной асимптотой графика функции y=f(x), при х®+¥ или х®-¥, если…

Исследование функции.

2) исследовать функцию на чётность, нечётность (в том случае, если область определения симметричное относительное нуля множество), периодичность (в… 3) найти точки пересечения графика функции с осями координат; 4) с помощью первой производной исследовать функцию на возрастание, убывание, найти точки экстремума;

Лекция 12

 

Первообразная

Восстановление функции по известной производной этой функции составляет одну из основных задач интегрального исчисления.   Определение 1:Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений…

Неопределённый интеграл.

При этом функция f(x) называется подынтегральной функцией,… Символ обозначает, таким образом, совокупность всех первообразных для функции f(x).

Свойства неопределённого интеграла.

Свойство 1:Производная неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному… Свойство 2:Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной…

Основные методы интегрирования.

2) Метод подстановки; 3) Метод интегрирования по частям.  

Таблица неопределённых интегралов некоторых функций.

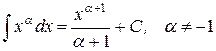
1.)	2.)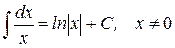
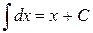
3.)	4.)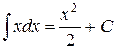
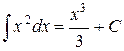
5.)	6.)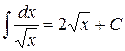
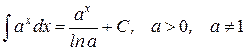
7.)	8.)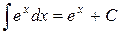
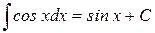
9.)	10.)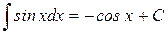
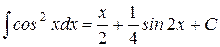
11.)	12.)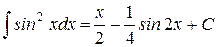
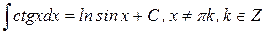
13.)	14.)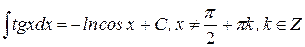
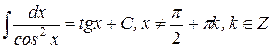
15.)	16.)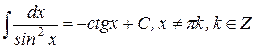
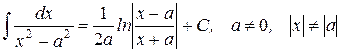
17.)	18.)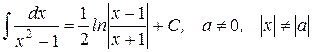
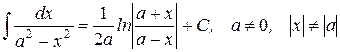
19.)	20.)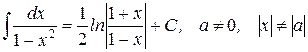
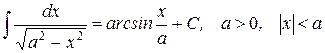
21.)	22.)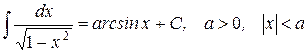
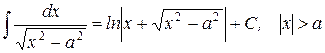
23.)	24.)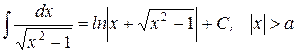
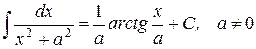
25.)	26.)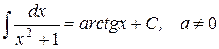
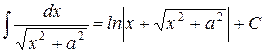
27.)	28.)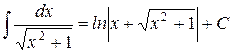

Основные свойства неопределённого интеграла.

Основные методы интегрирования.

Основные свойства определённого интеграла.

Формула Ньютона Лейбница.

 

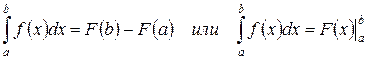
Замена переменной в определённом интеграле:

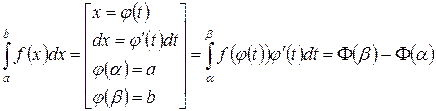
Интегрирование по частям в определённом интеграле:

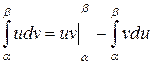
Лекция 13

Интегрирование рациональных функций.

Задача интегрирования рациональной функции сводится к нахождению интегралов следующих четырёх типов:

Ответ:, где С=const

 

Интегрирование некоторых тригонометрических выражений.

Правило 1: Для вычисления интегралов вида:

Тригонометрические подстановки.

Для подынтегральных выражений, содержащих радикалы, а также их квадраты удобны тригонометрические подстановки:

Интегралы вида .

Интегралы вида:

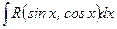
рационализируются подстановкой:

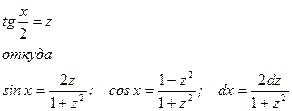
Некоторые интегралы, зависящие от радикалов.

Аналогично определяется рациональная функция трёх переменных R(x; y; z), четырёх и т.д. Интеграл вида

Подстановки Эйлера.

рационализируются одной из подстановок Эйлера:  

Определённый интеграл.

Обозначим это разбиение через t, а точки x0, x1, x2, …, xn, будем называть точками разбиения. В каждом из полученных частичных отрезков [хi-1, хi]… Геометрический смысл суммы s: сумма площадей прямоугольников с основаниями… Определение 1:Если существует конечный предел I интегральной суммы при (l®0 – наибольшая из длин всех частичных…

Основные свойства определённого интеграла.

· Если а>b, то ; · Каковы бы ни были числа а, b и с, всегда имеет место равенство: ; · Постоянный множитель можно выносить за знак определённого интеграла: ;

Формула Ньютона Лейбница.

Замена переменной в определённом интеграле:

Геометрические приложения определённого интеграла.

Площадь криволинейной трапеции:

· в прямоугольных координатах;

· в полярных координатах.

Объём тела вращения.

 

Несобственные интегралы.

  Рассмотрим так называемые несобственные интегралы, то есть определённый… В таких интегралах сверх предельного перехода выполняется ещё один, то есть осуществляется двукратный переход к…

Интеграл с бесконечным промежутком интегрирования

Пусть функция f(x) непрерывна на промежутке [а, +¥). Если существует конечный предел , то его называют несобственным интегралом первого рода и… Если интеграл имеет конечный предел, то говорят, что несобственный интеграл сходится;

Интеграл функции, имеющей разрыв

Пусть функция f(x) имеет разрыв в точке х=b, а остальных точках этого промежутка (а; b) она непрерывна. Если существует конечный предел , то его… Аналогично определяется несобственный интеграл, когда функция f(x) имеет разрыв в точке х=а:

Лекция 14

Понятие числового ряда.

называется числовым рядом или просто рядом. Числа а1, а2, а3, ..., аn ...… S1=а1, S2=а1+а2, S3=а1+а2+а3,…, Sn=а1+а2+а3+…+аn,

Свойства сходящихся рядов.

  Установлено, что сходящиеся ряды можно умножать на число, почленно складывать… · Если сходится ряд: и его сумма равна S, то и ряд где С=const, сходится и его сумма равна cS.

Достаточные признаки сходимости положительных рядов

Признаки сравнения: · (сходимости) - Пусть даны два ряда с неотрицательными членами и и для всех… · (расходимости) - Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство . Тогда если…

Знакопеременный ряд. Признак Лейбница

Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться… 1) ; 2) .

Абсолютная и условная сходимость

Остаток данного ряда (1) по абсолютному значению не превосходит соответствующего остатка ряда (2). Сумма S данного ряда(1) по абсолютному значению не превосходит суммы S' ряда…  

Ответ: ряд сходится.

·

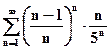
Применим признак Коши для положительного ряда:

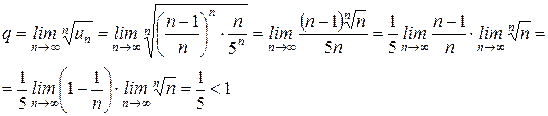
Ответ: ряд сходится.

·

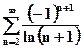
Применим признак Лейбница для знакопеременного ряда. Так как члены ряда стремятся к нулю всё время убывая по абсолютному значению, следовательно, ряд сходится:

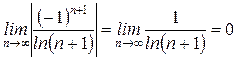
Ответ: ряд сходится.

Применим признак сравнения: Сравним данный ряд с рядом . Применяя интегральный признак сходимости, вычисляем интеграл:

Ответ: ряд расходится.

Лекция 15

Степенной ряд.

а также ряд более общего вида (2): ао+а1(х-х0)+а2х2(х-х0) 2+...+апхп(х-х0) n+..., говорят, что он расположен соответственно по степеням х, о или по степеням х -… Постоянные а0, a1, ... , ап, ... называются коэффи­циентами степенного ряда.

Промежуток и радиус сходимости степенного ряда, расположенного по степеням х

Теорема 1. Область сходимости степенного ряда есть некоторый промежуток (-R, R), симметричный относительно точки х=0. Иногда в него надо вклю­чить…   Промежуток (-R, R) называется промежутком сходимости, положительное число R — радиусом схо­димости степенного ряда.…

Промежуток и радиус сходимости степенного ряда, расположенного по степеням х-а

Теорема 2. Радиус сходимости R степенного ряда, расположенногопо степеням х-а равен пределу отношения при условии, что этот предел (конечный или…  

Разложение функций в степенной ряд

Если функция f(x) разлагается в степенной ряд, то разложение единственно. Разложение простейших функций по степеням х: · показательные (2);

Ряд Тейлора

 

Лекция 16

Дифференциальные уравнения. Основные понятия

Дифференциальным уравнением называется урав­нение, содержащее производные неизвестной функ­ции (или нескольких неизвестных функций). Вместо производных могут содержаться дифференциалы.

Если неизвестные функции зависят от одного ар­гумента, то дифференциальное уравнение называется обыкновенным, если от нескольких, то уравнение на­зывается дифференциальным уравнением с частными производными. Будем рассматривать только обык­новенные дифференциальные уравнения.

Общий вид дифференциального уравнения с одной неизвестной функцией таков:

F(х, у, у', у", ..., у⁽ⁿ⁾) = 0.

Порядком дифференциального уравнения называ­ется порядок наивысшей из производных, входящих в это уравнение.

Функция у=j(х) называется решением дифферен­циального уравнения, если последнее обращается в тождество после подстановки у=j(х).

Основной задачей теории дифференциальных уравнений является нахождение всех решений данно­го дифференциального уравнения. В простейших слу­чаях эта задача сводится к вычислению интеграла. Поэтому решение дифференциального уравнения на­зывают также его интегралом, а процесс нахождения всех решений — интегрированием дифференциально­го уравнения.

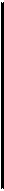
Вообще интегралом данного дифференциального уравнения называют всякое уравнение, не содержа­щее производных, из которого данное дифференциаль­ное уравнение вытекает как следствие.

 

Дифференциальные уравнения первого порядка

Если уравнение можно разрешить относительно у', то оно принимает вид: y' = f(x,y) и называется уравнением первого порядка, разрешенным относи­тельно… Дифференциальное уравнение удобно записать в виде: , являющемся част­ным… Уравнение в симмет­ричной форме удобно тем, что переменные х и у в нем равно­правны, т.е. каждую из них можно…

ДУ I порядка. Уравнения с разделяющимися переменными

Если ДУ I имеет вид: Р(х)dx+Q(y)dy=0, в котором Р зависит только от х, а Q зависит только от у, то оно является ДУ I с разделёнными переменными.

Общий интеграл уравнения с разделёнными переменными представляется уравнением:

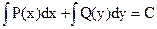
Если ДУ I имеет вид: X₁Y₁dy+X₂Y₂dx=0, в котором X₁ и X₂ зависят только от х, а Y₁ и Y₂ зависят только от у, то оно является ДУ I с разделяющимися переменными и приводится к ДУ I с разделёнными переменными. Процесс приведения называется разделением переменных.

 

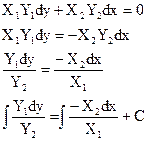
§70 Однородное ДУ I порядка (ОДУ I )

Пусть ДУ I имеет вид: Мdx+Ndy=0 – оно называется однородным ОДУ I, если отношение ^M/_N можно представить как функцию отношения ^y/_x. Это отношение обозначим через t:

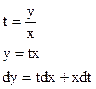
Тогда с помощью данной подстановки ОДУ I приводится к уравнению с разделяющимися переменными.

 

Лекция 17

§71 Линейное ДУ I порядка (ЛДУ I) Пусть ДУ I имеет вид: Мdx+Ndy=0 – оно называется ЛДУ I, если отношение M/N…  

Метод Бернулли.

y=u·v y¢=u¢·v+u·v¢ Подставляя выражения у и у¢ в заданное уравнение получаем:

Метод Лагранжа (метод вариации постоянной).

Составим вспомогательное ЛОДУ I у¢+Р(x)у=0 и решим его как уравнение с разделяющимися переменными. То есть получим, что у=f(x)+C, где С=const –… Теперь будем искать общее решение заданного уравнения в виде у=f(x)+C(х), где… Найдём производную полученного выражения у¢ и подставим у и у¢ в заданное уравнение из которого выразим…

Случаи понижения порядка

Иногда ДУ II или более высокого порядков допускает понижение порядка. Рассмотрим два случая:

Случай I: уравнение не содержит у.

Тогда в качестве неизвестной функции берётся величина у¢, а за аргумент принимаем х. При этом производные второго и высших порядков преобразуем по формулам:

 

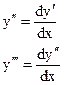
Случай II: уравнение не содержит х.

Тогда в качестве неизвестной функции берётся величина у¢, а за аргумент принимаем у. При этом производные второго и высших порядков преобразуем по формулам:

 

 

ЛДУ II

ЛДУ II называется уравнение вида: у²+Р(x)у¢+Q(x)у=R(x), где функции Р(х), Q(x), R(x) не зависят от х.

Если R(x)=0, то уравнение называется уравнением без правой части или однородным ЛОДУ II.

Если R(x)≠0, то уравнение называется уравнением с правой части или неоднородным ЛНДУ II.

 

ЛОДУ II с постоянными коэффициентами.

ау²+bу¢+cу=0, где а, b, c – некоторые постоянные. Составим характеристическое уравнение аk2+bk+c=0, которое в зависимости от D… · если D>0, то аk2+bk+c=0 имеет два различных действительных корня k1 и k2, тогда ЛОДУ II имеет общее решение…

ЛНДУ II с постоянными коэффициентами.

ау²+bу¢+cу=R(x), где а, b, c – некоторые постоянные. Его общее решение имеет вид: , где - общее решение ЛОДУ II ау²+bу¢+cу=0;

Свойства сходящихся рядов.

  Сходящиеся ряды можно умножать на число, почленно складывать и вычитать так… · Если сходится ряд: и его сумма равна S, то и ряд где С=const, сходится и его сумма равна СS.

Достаточные признаки сходимости положительных рядов

Признаки сравнения: · (сходимости) - Пусть даны два ряда с неотрицательными членами и и для всех… · (расходимости) - Пусть даны два ряда с неотрицательными членами и и для всех n выполняется неравенство . Тогда если…

Знакопеременный ряд. Признак Лейбница

Признак Лейбница: Знакопеременный ряд сходится, если его члены стремятся к нулю всё время убывая по абсолютному значению. Итак, должны выполняться… 3) ; 4) .

Степенной ряд.

а также ряд более общего вида (2): ао+а1(х-х0)+а2х2(х-х0) 2+...+апхп(х-х0) n+..., говорят, что он расположен соответственно по степеням х, или по степеням х -…  

Расположенного по степеням х

Теорема Область сходимости степенного ряда, расположенного по степеням х есть (-R, R), симметричный относительно точки х=0. Иногда в него надо…   Промежуток (-R, R) называется промежутком сходимости, положительное число R — радиусом сходимости степенного ряда.…

Расположенного по степеням х-а

Теорема Область сходимости степенного ряда, расположенного по степеням х-а есть некоторый промежуток (-R+а R+а), симметричный относительно точки…    

Дифференциальные уравнения первого порядка

Если уравнение можно разрешить относительно у', то оно принимает вид: y'=f(x, y) и называется уравнением первого порядка, разрешенным относительно… Дифференциальное уравнение удобно записать в виде: , являющемся частным… Уравнение в симметричной форме удобно тем, что переменные х и у в нем равноправны, т.е. каждую из них можно…

Уравнения с разделяющимися переменными

Если ДУ−I имеет вид: Р(х)dx+Q(y)dy=0, в котором Р зависит только от х, а Q зависит только от у, то оно является ДУ−I с разделёнными переменными.

Общий интеграл уравнения с разделёнными переменными представляется уравнением:

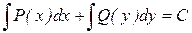
Если ДУ−I имеет вид: X₁Y₁dy+X₂Y₂dx=0, в котором X₁ и X₂ зависят только от х, а Y₁ и Y₂ зависят только от у, то оно является ДУ−I с разделяющимися переменными и приводится к ДУ−I с разделёнными переменными. Процесс приведения называется разделением переменных.

Линейное ДУ−I порядка (ЛДУ−I)

Пусть ДУ−I имеет вид: Мdx+Ndy=0 – оно называется ЛДУ−I, если отношение ^M/_N содержит у лишь в первой степени. ЛДУ−I принято записывать в виде у¢+Р(x)у=Q(x) где Р(x) и Q(x) непрерывные функции от х.

· Если Q(x)=0, то уравнение принимает вид у¢+Р(x)у=0 и оно называется ЛОДУ−I или линейным уравнением без правой части. В этом случае оно приводится к уравнению с разделяющимися переменными.

· Если Q(x)≠0, то уравнение называется ЛНДУ−I или линейным уравнением с правой части. В этом случае его можно решить методом Бернулли или методом Лагранжа.

Метод Бернулли.

y=u·v y¢=u¢·v+u·v¢ Подставляя выражения у и у¢ в заданное уравнение получаем:

Метод Лагранжа (метод вариации постоянной).

Составим вспомогательное ЛОДУ−I у¢+Р(x)у=0 и решим его как уравнение с разделяющимися переменными. То есть получим, что у=f(x)+C, где… Теперь будем искать общее решение заданного уравнения в виде у=f(x)+C(х), где… Найдём производную полученного выражения у¢ и подставим у и у¢ в заданное уравнение из которого выразим…

ЛОДУ−II с постоянными коэффициентами.

Составим характеристическое уравнение аk2+bk+c=0, которое в зависимости от D может иметь различные решения. · если D>0, то аk2+bk+c=0 имеет два различных действительных корня k1 и…

ЛНДУ−II с постоянными коэффициентами.

Его общее решение имеет вид: , где - общее решение ЛОДУ−II ау²+bу¢+cу=0; - частное решение ЛНДУ−II ау²+bу¢+cу=R(x), которое ищется, в зависимости от правой части по одному из…