рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Полиграфия
- /
- ДОКЛАД по дисциплине Теория игр и исследование операций На тему: Теория игр, графический метод в теории игр
Реферат Курсовая Конспект
ДОКЛАД по дисциплине Теория игр и исследование операций На тему: Теория игр, графический метод в теории игр
ДОКЛАД по дисциплине Теория игр и исследование операций На тему: Теория игр, графический метод в теории игр - раздел Полиграфия, Минобрнауки России Фгбоу Впо «Восточ...
МИНОБРНАУКИ РОССИИ
ФГБОУ ВПО «ВОСТОЧНО-СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ТЕХНОЛОГИЙИ УПРАВЛЕНИЯ»
Кафедра «Финансы и кредит»
ДОКЛАД
по дисциплине «Теория игр и исследование операций»
На тему: Теория игр, графический метод в теории игр
Выполнил: студент Д542 гр.
Подшивалова О.Д.
Научный руководитель:
Юмова С.Ж.
Улан-Удэ
Содержание
| 1. Введение 2. Основные методы решений 2.1.Основные понятия теории игр 2.2.Матричные игры 2.3.Решение матричной игры в чистых стратегиях 2.4.Принцип доминирования 2.5.Решение матричной игры 2×2 в смешанных стратегиях 3. Геометрическое решение игры 3.1.Решение игр с платежной матрицей 2×n 3.2.Решение игр с платежной матрицей m×2 4. Практическая часть 5. Заключение 6. Список литературы |
Введение
Непрерывное и последовательное развитие социалистического общества, его производительных сил и производительных отношений, повышение эффективности общественного производства непрерывно связанно с совершенствование системы планирования и управления. Современные достижения науки и техники все шире используются в практике для получения научно обоснованных наиболее эффективных решений в сфере планирования и управления.
При решении ряда практических задач (в разных областях деятельности) приходится анализировать ситуации, где налицо две ( или более) враждующие стороны, преследующие противоположные цели, причем результат каждого мероприятия одной из сторон зависит от того, какой образ действия выберет противник.
Необходимость анализировать подобные ситуации вызвала к жизни специальные математический аппарат. Теория игр по существу представляет собой не что иное, как математическую теорию конфликтных ситуаций.
Целью данной работы является рассмотрение не только теории игр в общем, но и ее графический метод решения.
Для наиболее оптимального изучения и рассмотрения поставлены следующие задачи:
1. Кратко изложить понятие о теории игр в целом;
2. Рассмотреть основные методы решений задач теории игр;
3. Детально изучить графический метод решения задач теории игр.
4. Привести примеры задач, решенных с помощью этого метода..
Основные методы решений
Основные понятия теории игр
Многие социально-экономические ситуации, в которых рассматриваются вопросы о выборе решения, обладают тем свойством, что в них сталкиваются не мнение двух сторон с различными интересами, каждая из которых для достижения своей цели имеет возможность действовать различными способами,
выбор которых при некоторых условиях может осуществляться в зависимости от
действий противоборствующей стороны. Такие ситуации называют конфликтными.
Математическая модель конфликтной ситуации называется игрой. Теория игр занимается математическими моделями принятия оптимальных решений в условиях конфликта. Любое возможное в игре действие игрока называется его стратегией. Игра называется конечной, если множество стратегий каждого игрока конечно. В противном случае (т.е. когда множество стратегий хотя бы одного игрока бесконечно), игра называется бесконечной. В дальнейшем будем рассматривать только конечные игры двух лиц.
Основной целью теории игр является выявление для каждого из игроков «оптимальных стратегий».
Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или, эквивалентно, минимально возможный средний проигрыш). Выбор оптимальной стратегии базируется на принципе, предполагающем, что оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его цели. Таким образом, теория игр абстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам, реальных конфликтах.
Будем считать, что выигрыш одного игрока равен в точности проигрышу
второго игрока, такая игра называется игрой с нулевой суммой. Конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока, называется биматричной игрой.
Матричные игры
суммой, в которой задается выигрыш игрока 1 в виде матрицы, строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру… находится выигрыш игрока 1, соответствующий применяемым стратегиям.Решение матричной игры в чистых стратегиях
Рассмотрим матричную игру с игроками P1 и P2 и платежной матрицей

1) Перед игроком P1 стоит задача выбора чистой стратегии, в результате применения которой он получит максимально возможный гарантированный
выигрыш. Если игрок P1 выбрал стратегию  , то его выигрышем может быть один из выигрышей
, то его выигрышем может быть один из выигрышей 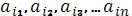 , расположенный в i-ой строке платежной
, расположенный в i-ой строке платежной
матрицы, в зависимости от выбранной стратегии игроком P2. Предполагая поведение игрока P1 крайне осмысленным, необходимо считать, что игрок P2 сыграет наилучшим для себя образом и на выбор игроком P1 стратегии Xi выберет ту стратегию Yj, при которой выигрыш игрока P1 окажется минимальным.
Обозначим минимальный среди выигрышей через αi:
 , (αi –показатель эффективности стратегии Xi).
, (αi –показатель эффективности стратегии Xi).
Продолжая действовать разумно, игрок P1 должен выбрать ту стратегию,
которая максимизирует показатель эффективности, т.е. для которой число αi максимально.
Обозначим: 
Число α называется нижней ценой игры в чистых стратегиях, а стратегия
Xi0, которая максимизирует показатель эффективности αi называется максиминной стратегией игрока P1.
Таким образом, если игрок P1 в игре будет следовать максиминной стратегии, то ему при любой игре противника P2 гарантирован выигрыш в чистых стратегиях, не меньший α.
2) Рассмотрим игру с точки зрения игрока P2, который стремиться минимизировать выигрыш игрока P1. Если P2 выберет стратегию 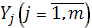 , то выигрышем игрока P1 может быть один из выигрышей
, то выигрышем игрока P1 может быть один из выигрышей 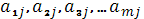 . Но так как игрок P2 предполагает, что игрок P1 играет наилучшим для себя образом, то выигрышем игрока P1 будет максимальное из этих чисел, обозначим βj:
. Но так как игрок P2 предполагает, что игрок P1 играет наилучшим для себя образом, то выигрышем игрока P1 будет максимальное из этих чисел, обозначим βj:
 (βj –показатель неэффективности стратегии Yj).
(βj –показатель неэффективности стратегии Yj).
Таким образом, для любой стратегии Yj игрока P2 наибольший его проигрыш равен βj. В интересах игрока P2 выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел βj обозначим β:

Число β называется верхней ценой игры в чистых стратегиях, а стратегия Yj0, которая максимизирует показатель неэффективности βj называется минимаксной стратегией игрока P2.
Теорема 3. Для элементов платежной матрицы имеют место неравенства:
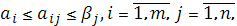 и, следовательно, нижняя цена игры не больше ее верхней цены в чистых стратегиях:
и, следовательно, нижняя цена игры не больше ее верхней цены в чистых стратегиях: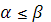 .
.
Пример. Найти решение игры, заданной платежной матрицей.

Решение:
Решим игру. Пусть  – оптимальная стратегия первого игрока,
– оптимальная стратегия первого игрока, 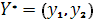 – оптимальная стратегия второго игрока, v – цена игры.
– оптимальная стратегия второго игрока, v – цена игры.
Рассмотрим матрицу
min
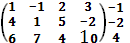 max(-1,-2,4)=4=
max(-1,-2,4)=4=
max 6 7 4 10
min (6,7,5,10)=5=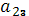
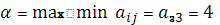 - нижняя цена игры.
- нижняя цена игры.
 - верхняя цена игры.
- верхняя цена игры.
 - максиминная стратегия,
- максиминная стратегия, 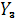 - минимаксная стратегия
- минимаксная стратегия
Если  то элемент
то элемент  называется седловым элементом матрицы
называется седловым элементом матрицы
A=
Теорема 4. (о разрешимости матричной игры в чистых стратегиях) Если платежная матрица A имеет седловой элемент  , то матричная игра имеет решение в чистых стратегиях, при этом оптимальной стратегий первого игрока является Xi0 чистая стратегия, а для второго – Yj0 чистая стратегия, а цена игры v =
, то матричная игра имеет решение в чистых стратегиях, при этом оптимальной стратегий первого игрока является Xi0 чистая стратегия, а для второго – Yj0 чистая стратегия, а цена игры v =  .
.
Пример. Найти решение игры, заданной платежной матрицей A=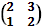
Решение:
Решим игру. Пусть  -оптимальная стратегия первого игрока,
-оптимальная стратегия первого игрока, 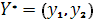 - оптимальная стратегия второго игрока, v – цена игры.
- оптимальная стратегия второго игрока, v – цена игры.
Рассмотрим матрицу
min
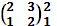
max 2 3
 v=
v= =2 цена игры v = 2 , существует седловой элемент
=2 цена игры v = 2 , существует седловой элемент  =
= , тогда решение в чистых стратегиях имеет вид:
, тогда решение в чистых стратегиях имеет вид:
оптимальная стратегия первого игрока: 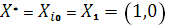
оптимальная стратегия второго игрока: 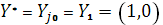
Ответ: оптимальные стратегии игроков 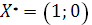 ;
;  , цена игры v =2 .
, цена игры v =2 .
Принцип доминирования
A=. Если ,то говорят, что j-ая строка доминируется i-ой строкой, при этом i-ая… Если , то говорят, что i-ый столбец доминируется j-ым столбцом, при этом j-ый столбец называется доминирующим для…Решение матричной игры 2×2 в смешанных стратегиях
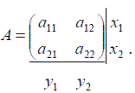
Решить игру с платежной матрицей
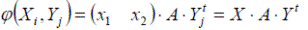
Платежная функция
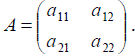
Решить игру с платежной матрицей
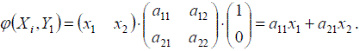
Положим 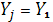 . Тогда
. Тогда

 . Тогда
. Тогда
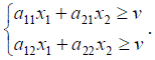 Если
Если  - оптимальная стратегия первого игрока, то по определению
- оптимальная стратегия первого игрока, то по определению
решения матричной игры
 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то ( -цена игры).
-цена игры).
Решая систему, получим  .
.

Аналогично для второго игрока:

 Тогда
Тогда
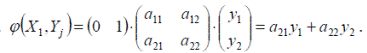
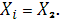 Тогда
Тогда
Если 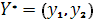 - оптимальная стратегия второго игрока.
- оптимальная стратегия второго игрока.
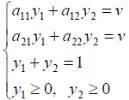 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то ( -цена игры).
-цена игры).
Решая систему, получим  .
.
Пример. Найти решение игры заданной платежной матрицей A= 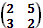 .
.
Решение:
Решим игру. Пусть  - оптимальная стратегия первого игрока,
- оптимальная стратегия первого игрока, 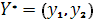 - оптимальная стратегия второго игрока,
- оптимальная стратегия второго игрока, -цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
-цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
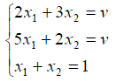

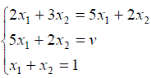
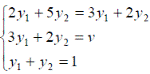


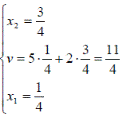



Ответ: оптимальные стратегии игроков  , цена игры
, цена игры  .
.
Геометрическое решение игры
Решение игр с платежной матрицей 2×n
Решить игру с платежной матрицей A=
Алгоритм:
1) Через концы горизонтального отрезка [0;1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0;1] будем ставить некоторую смешанную стратегию (x;1− x).
2) На левом перпендикуляре от точки 0 отложить элементы 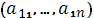 . На правом перпендикуляре от точки 1 отложить элементы
. На правом перпендикуляре от точки 1 отложить элементы  .
.
Замечание. Масштабы на левом и правом перпендикулярах должны быть
одинаковы, не обязательно совпадающие с масштабом горизонтального отрезка [0;1].
3) Соединить отрезками элементы .
4) Выделить нижнюю огибающую всех построенных отрезков, и найти максимальную точку (точки). Пусть точка является пересечением отрезков 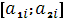 и
и 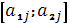 . Тогда оптимальную стратегию можно найти при помощи матрицы
. Тогда оптимальную стратегию можно найти при помощи матрицы 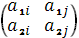 .
.
Решить игру с платежной матрицей A= графически.
графически.
Решение:
1. Через концы горизонтального отрезка [0;1] проведем 2 перпендикуляра к нему. Каждой точке отрезка [0;1] будем ставить смешанную стратегию (x; 1− x).
2. На левом перпендикуляре от точки 0 отложить элементы 2, 3, 11. На правом перпендикуляре от точки 1 отложить элементы 7, 5, 2.
3. Соединить отрезками элементы 2 и 7, 3 и 5, 11 и 2.

4. Выделим нижнюю огибающую всех построенных отрезков, и найдем
максимальную точку. Точка является пересечением отрезков [3;5] и [11;2]. Тогда оптимальную стратегию можно найти при помощи матрицы  .
.
Решим игру с платежной матрицей  .
.
Оптимальные стратегии игроков и цену игры можно найти, решив системы:
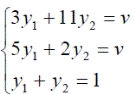
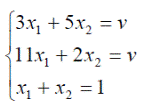

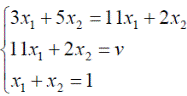
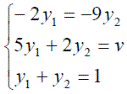
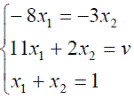
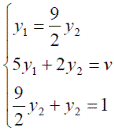
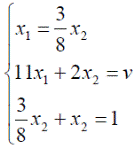
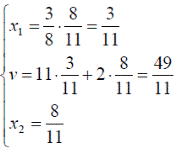
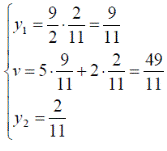
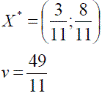
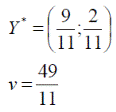
Ответ: оптимальные стратегии игроков оптимальные стратегии игроков 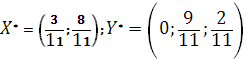 , цена игры
, цена игры 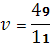
Решение игр с платежной матрицей m×2
Решить игру с платежной матрицей A=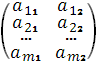 .
.
Алгоритм:
1) Через концы горизонтального отрезка [0;1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0;1] будем ставить некоторую смешанную стратегию (y;1− y).
2) На левом перпендикуляре от точки 0 отложить элементы  . На правом перпендикуляре от точки 1 отложить элементы
. На правом перпендикуляре от точки 1 отложить элементы 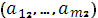 .
.
3) Соединить отрезками элементы .
4) Выделить верхнюю огибающую всех построенных отрезков, и найти минимальную точку (точки). Пусть точка является пересечением отрезков Тогда оптимальную стратегию можно найти при помощи матрицы 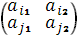 .
.
Пример. Решить игру с платежной матрицей A= .
.
Решение:
Решим графическим методом.
1. Через концы горизонтального отрезка [0;1] проведем 2 перпендикуляра к нему. Каждой точке отрезка [0;1] будем ставить смешанную стратегию (y; 1− y).
2. На левом перпендикуляре от точки 0 отложить элементы 6, 4, 2, 1. На правом перпендикуляре от точки 1 отложить элементы 5, 6, 7, 8.
3. Соединить отрезками элементы 6 и 5, 4 и 6, 2 и 7, 1 и 8.
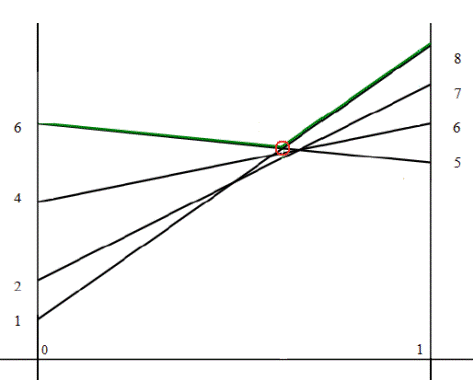
4. Выделим верхнюю огибающую всех построенных отрезков, и найдем минимальную точку. Точка является пересечением отрезков [6;5] и [1;8]. Тогда оптимальную стратегию можно найти при помощи матрицы 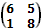 .
.
Решим игру с платежной матрицей 

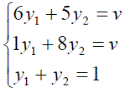
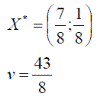
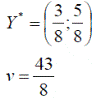
Ответ: оптимальные стратегии игроков оптимальные стратегии игроков 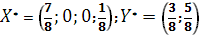 , цена игры
, цена игры 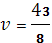
Практическая Часть
1.1 По формулам Крамера Решение.Заключение
На основании проведенного исследования можно сделать следующие выводы:
· Теория игр является очень сложной областью знания. При обращении к ней надо соблюдать осторожность и четко знать границы применения.
· Теория игр пытается предсказать результат на основе интерактивных моделей, в которых решения каждой стороны влияют на решения других сторон.
· Смысл «игры» здесь является следующим: действие со стороны одного игрока приводит к действиям со стороны других.
· Теория игр полезна, когда требуется определить наиболее важные и требующие учета факторы в ситуации принятия решений в условиях конкурентной борьбы.
Графический метод является одним из основных методов решения задач теории игр. Главной особенностью этого метода является графической изображение задачи. Именно эта особенность и делает этот метод наиболее простым для восприятия человеком задачи, которую ему нужно решить.
Литература
1.Просветов Г. И. Математические методы в экономике: Учебно-методическое
пособие. – М.: Изд-во РДЛ, 2012.
2. Бережная Е. В., Бережной В. И. Математические методы моделирования
экономических систем: Учеб пособие. – М.: Финансы и статистика, 2011.
3. Экономико-математическое моделирование. / Под ред. И. Н. Дрогобыцкого. –
М.: Изд-во «Экзамен», 2013.
4. Гончарова Г. А., Молчалин А. А. Элементы дискретной математики: Учебное
пособие. – М.: ФОРУМ: ИНФРА-М, 2004.
5. Высшая математика для экономистов: Учебник / Под ред Н. Ш. Кремера –
М.: ЮНИТИ, 2011.
– Конец работы –
Используемые теги: Доклад, дисциплине, Теория, игр, исследование, операций, тему, Теория, игр, Графический, метод, Теории, игр0.097
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ДОКЛАД по дисциплине Теория игр и исследование операций На тему: Теория игр, графический метод в теории игр
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов