рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- По курсу Теория информационных процессов и систем
Реферат Курсовая Конспект
По курсу Теория информационных процессов и систем
По курсу Теория информационных процессов и систем - раздел Философия, Министерство ...
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский государственный институт электроники и математики
(Технический университет)
Кафедра математического обеспечения систем обработки информации и управления
Методические указания к лабораторным работам
По курсу
«Теория информационных процессов и систем»
Москва 2011
Теория информационных процессов и систем
ЛАБОРАТОРНАЯ РАБОТА.
Тема: Помехоустйчивое кодирование.
ЗАДАНИЕ
Построить помехоустойчивый циклический код. В качестве порождающего многочлена кода взять неприводимый примитивный полином g(x) из таблицы вариантов.
1. По заданному полиному построить порождающую и проверочную матрицы в систематическом виде.
2. Оценить корректирующую способность построенного кода и рассчитать характеристики его помехоустойчивости при заданной вероятности искажения одного символа кода.
3. Разработать алгоритм и программу защиты от искажений под воздействием помех данных из текстового файла произвольной длины с помощью разработанного помехоустойчивого кода.
4. Смоделировать процесс прохождения полученного кода через двоичный симметричный канал связи с вероятностью искажения каждого симвода кода р из таблицы вариантов. Добавить несколько пакетов ошибок в середине слова и концевой.
5. Разработать алгоритм и программу декодирования искаженного в канале связи кода путем проверки наличия ошибки в каждом блоке и исправления ошибки по критерию наименьшего расстояния.
6. Сравнить файлы данных: исходный и полученный в результате декодирования, посчитать количество искаженных символов и сравнить его с характеристиками помехоустойчивости кода, вычисленными в п.2.
7. В зависимости от результатов предыдущего шага изменить характеристику канала связи – вероятность искажения р (увеличить, если качество передачи данных хорошее и уменьшить, если плохое) и повторить пункты 4-6. Сделать выводы о соответствии построенного кода характеристикам канала связи.
Варианты
Группа МС-71
| Вар. № | Тип кода | порождающий многочлен g(х) | Вероят-ть искажения р |
| Расширенный циклический код Хемминга | x4+ x+1 | 10-5 | |
| Циклический код Хемминга | x5+ x2+1 | 10-5 | |
| Расширенный циклический код Хемминга | x3+ x+1 | 10-3 | |
| Расширенный циклический код Хемминга | x4+ x3+1 | 10-4 | |
| Циклический код Хемминга | x3+ x+1 | 10-3 | |
| Циклический код Хемминга | x4+ x3+1 | 10-3 | |
| Расширенный циклический код Хемминга | x3+ x2+1 | 10-4 | |
| Расширенный циклический код Хемминга | x5+ x2+1 | 10-3 | |
| Циклический код Хемминга | x6+ x+1 | 10-3 | |
| Расширенный циклический код Хемминга | x4+ x+1 | 10-3 | |
| Циклический код Хемминга | x3+ x2+1 | 10-3 | |
| Циклический код Хемминга | x4+ x+1 | 10-4 |
Группа МС-72
| Вар. № | Тип кода | порождающий многочлен g(х) | Вероят-ть искажения р |
| Расширенный циклический код Хемминга | x4+ x3+1 | 10-3 | |
| Циклический код Хемминга | x3+ x2+1 | 10-4 | |
| Циклический код Хемминга | x6+ x+1 | 10-5 | |
| Циклический код Хемминга | x5+ x2+1 | 10-5 | |
| Расширенный циклический код Хемминга | x4+ x3+1 | 10-3 | |
| Расширенный циклический код Хемминга | x4+ x+1 | 10-5 | |
| Расширенный циклический код Хемминга | x3+ x+1 | 10-4 | |
| Расширенный циклический код Хемминга | x4+ x+1 | 10-4 | |
| Циклический код Хемминга | x6+ x+1 | ||
| Циклический код Хемминга | x4+ x+1 | 10-3 | |
| Расширенный циклический код Хемминга | x3+ x+1 | 10-5 | |
| Расширенный циклический код Хемминга | x3+ x2+1 | 10-3 | |
| Циклический код Хемминга | x5+ x2+1 | 10-3 |
3. Теоретические сведения
3.1. Помехоустойчивое кодирование
Кодирование, с помощью которого можно нейтрализовать непреднамеренное искажение информации, обусловленное, например, наличием шума в канале связи, называют помехоустойчивым. Оно используется для защиты информации от случайных искажений при хранении, передаче и т.п. Проблема обусловлена несоответствием между требованиями, предъявляемыми при передаче данных и качеством реальных каналов связи. В сетях передачи данных требуется обеспечить вероятность ошибки не выше 10-6 - 10-9, а при использовании реальных каналов связи указанная вероятность не превышает 10-2 - 10-5.
Определение. Помехоустойчивым (п/у) или корректирующим называется код, позволяющий обнаружить и устранить ошибки, возникающие под действием помех.
Теорема Шеннона для дискретного канала с помехами утверждает, что вероятность ошибок за счет действия в канале связи помех может быть сделана сколь угодно малой выбором соответствующего способа кодирования.
К сожалению основная теорема кодирования Шеннона не конструктивна, она не указывает способ построения конкретного оптимального помехоустойчивого кода, обеспечивающего предельное согласование сигнала с каналом, существование которого доказывает.
Вместе с тем, обосновав принципиальную возможность построения помехоустойчивых кодов, обеспечивающих идеальную передачу, теория Шеннона мобилизовала усилия ученых на разработку конкретных кодов. В результате в настоящее время теория помехоустойчивого кодирования превратилась в самостоятельную науку, в развитии которой достигнуты большие успехи.
Далее в этом разделе мы рассмотрим способы, позволяющие закодировать некое сообщение или какой-либо его код таким образом, чтобы можно было восстановить это сообщение в случае искажений за счет помех.
Помехоустойчивое кодирование бывает блочное и непрерывное.
- блочными называют коды, в которых исходные сообщения S объединяются в блоки и каждый блок кодируется помехоустойчивым кодом.
- при непрерывном кодировании построение помехоустойчивого кода ведется непрерывно по наблюдаемой части последовательности S не дожидаясь конца блока. Используется реже.
Блочные коды в свою очередь делятся на
- равномерные, использующие блоки равной длины и не требующие разделительного символа между ними;
- неравномерные, имеющие неопределенную длину блока.
- самый большой класс блочных равномерных кодов составляют линейные коды, у которых проверочные символы получаются в результате линейных операций над информационными символами.
Для двоичных кодов такой линейной операцией является Å - сложение по модулю два информационных символов.
Помехоустойчивость кодирования обеспечивается за счет введения избыточности в кодовые слова. Пусть длина блока равномерного кода равна n. Всего можно составить N0=2n различных кодовых слов такой длины. И пусть среди n символов блока:
k – используется для передачи информации, а остальные
m=n-k – являются проверочными и используются только для защиты от сбоев.
Такие блочные линейные коды называют (n,k)–кодами.
Процесс помехоустойчивого кодирования можно описать следующим образом. В последовательности {S}, поступающей на вход помехоустойчивого кодера все символы являются информационными. Поэтому разбиваем её на блоки по k символов. В процессе помехоустойчивого кодирования к каждому такому блоку добавляются по m проверочных символов. Полученные блоки длиной n символов составят помехоустойчивую последовательность {U}, передаваемую по каналу связи.
Если бы все символы блока были информационными, то каждый блок помехоустойчивого кода длиной n максимально мог бы нести количество информации равное  , а на самом деле несут информацию только k символов блока в максимально возможном количестве
, а на самом деле несут информацию только k символов блока в максимально возможном количестве 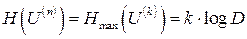 , тогда избыточность блока помехоустойчивого кода U длиной n равна
, тогда избыточность блока помехоустойчивого кода U длиной n равна
 .
.
Это значит, что из всех возможных N0=2n кодовых слов (комбинаций n двоичных символов кода) в качестве помехоустойчивого кода используется только часть слов и их количество равно N=2k.
Таким образом все множество {U} кодовых слов разбивается на два множества: разрешенные и запрещенные или ошибочные слова.
На вход канала связи поступают только разрешенные кодовые слова, а на выходе могут быть любые – как разрешенные, так и ошибочные слова.
Основная задача построения помехоустойчивых кодов – выбор их множества всех возможных кодовых слов такое подмножество разрешенных, чтобы вероятность обнаружения и исправления ошибки была максимально возможной, и, следовательно, вероятность искажения информации в канале связи была наименьшей.
3.2. Циклические коды
Код называется циклическим, если из того, что кодовое слово
U={ un-1, … , u1, u0}ÎMразр
принадлежит множеству разрешенных слов следует, что слово
 ={ un-2, … , u0, un-1,}ÎMразр,
={ un-2, … , u0, un-1,}ÎMразр,
 , полученное сдвигом cлова U влево по кругу тоже принадлежит множеству разрешенных слов.
, полученное сдвигом cлова U влево по кругу тоже принадлежит множеству разрешенных слов.
Циклический код является частным случаем полиномиальных кодов, в которых кодовое слово U={u0, u1, … ,un-1} представляется в виде полинома от фиктивной переменной x с коэффициентами, равными числам кода. Если код построен над полем GF(2)={0,1}, то коэффициенты многочлена - числа 0 или 1:
 .
.
Замечание. Степени фиктивной переменной x используются только для обозначения места соответствующей компоненты кодового вектора в регистре сдвига и никакой иной смысловой нагрузки не несут.
Например для кодового слова U=[1010101] значности n=7 полином имеет вид
 .
.
Над полиномами определены все арифметические операции по обычным правилам, в том числе и умножение в столбик и деление углом. При этом сложение и вычитание коэффициентов выполняется как суммирование по модулю два. Если степень результата превышает (n-1), то результат приводится по модулю полинома (хn+1).
Замечание. Результатом приведения одного полинома по модулю другого полинома является полином, являющийся остатком от деления первого на второй (модуль).
Циклическая перестановка соответствует умножению u(x) на x. В нашем случае:
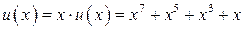 ,
,
 после приведения результата по модулю (хn+1) (то есть деления u(x) на (х7+1)), получаем
после приведения результата по модулю (хn+1) (то есть деления u(x) на (х7+1)), получаем
u` (x) =x5+ x3+ x+1 и u`=[0101011],
что соответствует сдвигу битов кодового слова влево по кругу на один разряд.
Таким образом, умножение на любой полином соответствует определенной последовательности циклических сдвигов кода и да дает полином, также соответствующий разрешенному кодовому слову. То есть множество разрешенных слов образует группу и циклический код является групповым.
Если не приводить полином, то при умножении полинома степени k на полином степени m степени полиномов складываются, и полином-результат имеет степень n=k+m. Исходное кодовое слово длины k при этом приобретает m новых разрядов, которые могут играть роль проверочных символов.
Циклический код это также блочный (n, k)-код, с длиной блока n, содержащий k информационных символов и m = n – k проверочных символов.
Операция кодирования для циклического кода состоит в умножении любого полинома p(x) степени k-1, соответствующего информационному подблоку на один и тот же полином g(x) степени (n-k), называемый образующим или порождающим или кодирующим полиномом (многочленом).
При этом число разрешенных кодовых слов остается прежним 2k, а общее число возможных кодовых слов становится равным 2n.
При декодировании выполняется деление на тот же образующий полином. При этом разрешенные кодовые слова делятся без остатка, а появление ненулевого остатка – это признак ошибки.
Ненулевой остаток от деления s(x) называется синдромным многочленом. Пусть вместо кодового слова U получено слово 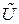 , которому соответствует многочлен
, которому соответствует многочлен  . При этом вектор ошибки e, содержащий единицы в ошибочных позициях может быть получен как e= U Å
. При этом вектор ошибки e, содержащий единицы в ошибочных позициях может быть получен как e= U Å 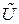 .
.
Синдромный многочлен, определяемый как остаток от деления на порождающий многочлен g(x) зависит только от вектора ошибок:
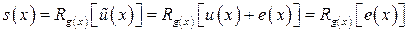 , так как
, так как  .
.
Этот факт используется при построении таблицы синдромов, применяемой при декодировании. Для всех возможных значений вектора ошибки e(x) вычисляются синдромы s(x) и записываются в таблицу. В процессе декодирования по синдрому s(x) находится соответствующий вектор ошибки e(x) и восстанавливается переданное слово как
u(x) = + e(x).
+ e(x).
Ошибка останется необнаруженной в том и только в том случае, если многочлен, соответствующий вектору ошибки делится на g(x) без остатка, то есть если вектор ошибки совпадет с разрешенным кодовым словом.
Таким образом, процесс декодирования циклических кодов (как и всех линейных блочных кодов) можно разбить на три этапа:
1. Вычисление синдрома
2. Определение ошибочных компонент принятого слова (вектора ошибки)
3. Исправление ошибки или выдача сообщения о наличии неисправимой ошибки
3.3. Циклические коды Хемминга
Циклические коды Хемминга образуют подмножество циклических (n, k) – кодов. Они обладают всеми свойствами кодов Хемминга и еще дополнительными полезными свойствами.
При определении методов построения циклических кодов используются понятия неприводимых и примитивных многочленов.
Определение. Многочлен g(х) степени m называется неприводимым в поле GF(2)={0, 1}, если он не делится ни на какой многочлен с коэффициентами из GF(2) степени меньшей m, но большей нуля.
Определение. Неприводимый многочлен g(х) степени m называется примитивным, если наименьшая степень n, при которой многочлен хn+ 1 делится на g(х) без остатка, равна n=2m-1.
Другими словами, многочлен g(х), степени m называется примитивным, если
 делится на g(х) без остатка,
делится на g(х) без остатка,
а 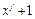 не делится на g(х) ни для какого значения
не делится на g(х) ни для какого значения 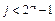 .
.
Например, многочлен 1 + х2 + х3 примитивен:
он делит х7 + 1, но не делит xj+1 при j < 7.
Примитивен также многочлен 1 + х3 + х4 :
он делит х15 + 1, но не делит xj+1 при j < 15.
С помощью порождающих многочленов g(х) можно строить порождающие и проверочные матрицы и таблицы синдромов для декодирования.
Утверждение. Для любого целого положительного числа m существует совершенный (n,k)-код Хэмминга, в котором n=2m-1 или k =2m-m-1.
Расширенные коды Хэмминга. Полезное расширение кодов Хэмминга заключается в дополнении кодовых векторов дополнительным двоичным разрядов так, чтобы число единиц в каждом кодовом слове было четным. Такие коды обладают двумя полеными свойствами:
1. Длины кодов увеличиваются с 2n-1 до 2n, что удобно с точки зрения хранения и передачи информации,
2. Минимальное расстояние для расширенных кодов Хэмминга равно четырем, а не трем, что позволяет обнаруживать трехкратные ошибки.
3.4. Критерии оценки помехоустойчивости.
В качестве численных характеристик помехоустойчивости кода используются:
1. Помехоустойчивость кода
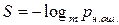
- собственное количество информации в факте необнаружения ошибки.
2. Коэффициент обнаружения
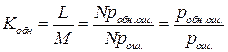 ,
,
где M – ожидаемое общее число искаженных кодовых слов,
L - ожидаемое число исправленных кодовых слов,
N – число всех кодовых слов,
рош. – число вероятность появления ошибки,
робн.ош. – вероятность обнаружения и исправления ошибки.
Если R - ожидаемое число неисправленных искаженных кодовых слов, то R=M-L и 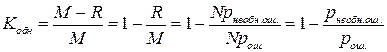 .
.
Пусть вероятность искажения одного символа кода равна р.Найдем вероятности передачи без ошибки р(0) и однократной ошибки р(1) при которых гарантируется правильная передача простым кодом Хемминга.
 .
.
(Для расширенного кода Хемминга выявляется и двухкратная ошибка с вероятностью  ).
).
Вероятность ошибочной передачи – все остальное. С учетом того, что при больших n: 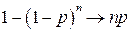 (по разложению (1-р)n в ряд Тейлора):
(по разложению (1-р)n в ряд Тейлора):
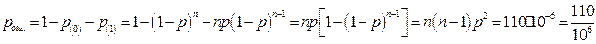
Если исправляется одна ошибка, то по теоремам Хемминга можно одновременно обнаружить 2 ошибки. Расширенный код Хемминга позволяет дополнительно обнаружить еще одну ошибку. Вероятность появления необнаруживаемых 3-х и 4-х кратных ошибок
 и
и  , где
, где  .
.
При малых значениях вероятности р при вычислении рнеобн.ош. ошибки большей кратности можно не учитывать в силу их малой вероятности.
3.5. Определение значности кода.
Первым шагом при построении кода являеся определение значности кода, то есть количества символов n в блоке помехоустойчивого кода и количества символов k исходного файла (информационных символов). Они определяют корректирующие способности кода. При этом каждый блок содержит m проверочных символов.
Для заданного образующего полинома степени m количество добавляемых при кодировании проверочных символов равно m. Коды Хемминга исправляют одиночную ошибку в блоке. Это коды с 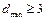 . Соотношения для параметров кода n, k и m для них имеют вид:
. Соотношения для параметров кода n, k и m для них имеют вид:
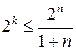 и
и 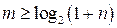 .
.
Отсюда длина блока выбирается из неравенства
n ≤ 2m – 1,
а количество информационных символов в блоке k = n - m.
Коды, удовлетворяющие этому условию являются квазисовершенными. Решить это уравнение относительно n здесь сложно, поэтому определим из него m=n-k:
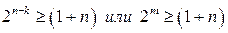 (*).
(*).
Таблица. Соотношения между параметрами помехоустойчивых кодов.
| n | … | … | … | … | |||||||||||||||||
| m | … | … | … | … | |||||||||||||||||
| k | … | … | … | … |
Для того чтобы количество информационных символов было максимальным при заданном количестве проверочных символов желательно выбирать общую длину блока n таким образом, чтобы неравенство (*) превратилось в строгое равенство. Коды, удовлетворяющие этому условию являются совершенными.
3.6. Матричное задание циклических кодов.
Циклический код может быть задан порождающей и проверочной матрицами. Для их построения достаточно знать порождающий g(x) и проверочный h(x) многочлены. При этом проверочный многочлен вычислякется по порождающему:
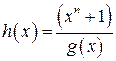
Для несистематического циклического кода матрицы строятся циклическим сдвигом порождающего и проверочного многочленов, т.е. путем их умножения на x.
При построении матрицы H(n,k) старший коэффициент многочлена h(x) располагается справа.
 и
и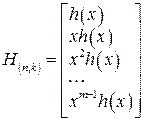
Например представим в матричном виде. циклический (7,4)-код с порождающим многочленом g(x)=x3+x+1 и проверочным многочленом
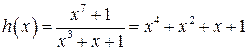 .
.
Порождающая G(7,4) и проверочная H(7,4) матрицы (n=7,k=4)-кода имеют вид:
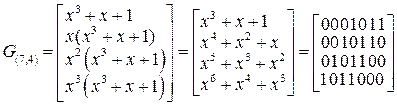
 ,
,
Построенные таким образом матрицы не имеют систематического вида. Для получения матрицы G(n,k) циклического кода в систематическом виде, то есть в виде 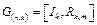 , где Ik - единичная матрица; Rk,m - прямоугольная матрица, необходимо найти матрицу Rk,m. Ее строки ri(x) (i=1, … ,.k) определяются следующими полиномами:
, где Ik - единичная матрица; Rk,m - прямоугольная матрица, необходимо найти матрицу Rk,m. Ее строки ri(x) (i=1, … ,.k) определяются следующими полиномами:
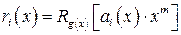 ,
,
где Rg(x)[ ] – обозначает операцию получения остатка от деления на g(x), и ai(x) – полином, соответствующий значению i-й строки матрицы Ik. Так как ai(x)=xk-i, то получаем, что ai(x)xm = xm+k-i = xn-i, то есть 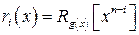 .
.
Для нашего примера. Матрица G(n,k) для (7,4)-кода на основе порождающего многочлена g(x)=x3+x+1 в систематическом виде  , строится так:
, строится так:
Поскольку 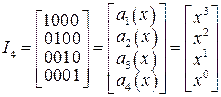 ,
,
 определим R4,3, используя формулу
определим R4,3, используя формулу 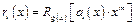 . Первую строку получаем делением
. Первую строку получаем делением
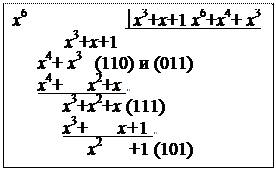 или
или
 Þ (101).
Þ (101).
Для получения второй строки не надо снова делить углом, так как делимое совпадет с предыдущим случаем с точностью до последнего нуля. Поэтому для получения остатка от деления на х5 достаточно взять предпоследний остаток в предыдущем делении на х6 не снося очередной нуль. Таким способом определяется 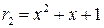 (111),
(111), 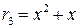 (110) и
(110) и 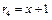 (011). Последние две строки получаются из одного и того же остатка, убирая последовательно по одному нулю (добавляя при необходимости слева нули до трех символов), так как в этой строке были при делении снесены два нуля.
(011). Последние две строки получаются из одного и того же остатка, убирая последовательно по одному нулю (добавляя при необходимости слева нули до трех символов), так как в этой строке были при делении снесены два нуля.
В результате получаем 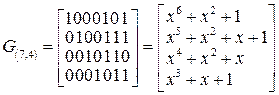
Количество исправляемых ошибок в блоке определяется минимальным рассстоянием Хемминга dmin между разрешенными кодовыми словами. Минимальное расстояние для (n,k)-кода равно наименьшему числу линейно зависимых столбцов проверочной матрицы. Для нашего примера dmin (5,3)=2.
Проверочная матрица в систематическом виде строится на основе матрицы G(n,k), а именно: 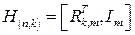 .
.
Для нашего примера. Для нашего кода матрица H(n,k) будет иметь вид:
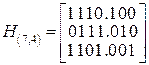 .
.
Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно  , где 0 – матрица размерности kxm, у которой все элементы равны нулю.
, где 0 – матрица размерности kxm, у которой все элементы равны нулю.
3.7. Кодирование и декодирование.
Кодирование при матричном представлении кода ведется путем умножения вектора, соответствующего информационному слову, на порождающую матрицу. Результат операции дает слово помехоустойчивого кода.
Для нашего примера кодирование блока информационных символов Р=[110] дает блок помехоустойчивого кода U =11010]:

Произведение любого разрешенного кодового слова U на транспонированную проверочную матрицу дает вектор длины (n-k) с нулевыми координатами
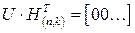 .
.
Для нашего кода это произведение дает 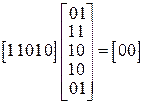 .
.
Таким образом проверка правильности принятого кода состоит в умножении вектора этого кода на проверочную матрицу. Нулевой вектор результата означает отсутствие ошибки передачи данных.
Произведение неразрешенного, т.е. с ошибкой, кодового слова 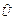 на транспонированную проверочную матрицу называется синдромным вектором и обозначается S.
на транспонированную проверочную матрицу называется синдромным вектором и обозначается S.
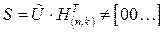
Появление отличного от нулевого синдромного вектора является признаком ошибки. В этом случае декодирование предполагает исправление ошибки или выдачу сообщения о неисправимой ошибке.
Например. Пусть при передаче кодового слова, полученного в предыдущем примере, допущена одна ошибка и принято 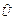 = [11000], то есть во втором символе ошибка. Соответствующий полином:
= [11000], то есть во втором символе ошибка. Соответствующий полином: 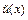 =x4+x3.
=x4+x3.
 Вычисляем синдром делением его на образующий полином g(x)=x3+x+1. Если нас интересует только остаток от деления, то можно вычислять его в столбик.
Вычисляем синдром делением его на образующий полином g(x)=x3+x+1. Если нас интересует только остаток от деления, то можно вычислять его в столбик.
| e(x) | 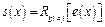
|
| x0=1 | |
| x | x |
| x2 | x2 |
| x3 | x+1 |
| x4 | x2+ x |
| x5 | x2+x+1 |
| x6 | x2+1 |
Составим таблицу синдромов для однократных ошибок. Все возможные вектора ошибок для искажений единственного символа в блоке будут иметь по одной единичной координате при всех остальных нулевых. Им соответствуют всевозможные одночлены, для которых вычисляем остатки от деления на и получается искомая таблица.
Замечание. при построении этой таблицы можно воспользоваться результатами деления xn на g(x), полученными при построении порождающей матрицы. Для синдромов, имеющих степень меньше m, синдромный полином совпадает с полиномом ошибки.
В нашем случае находим по таблице, что e(x) = x и исправляем ошибку:
u(x)=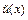 +e(x)=x4+x2+x+1.
+e(x)=x4+x2+x+1.
Появление синдромного вектора, не содержащегося в таблице, означает, что произошло более одной ошибки и требует соответствующего сообщения о неисправимой ошибке в блоке. Ошибка в блоке останется необнаруженной в том и только в том случае, если многочлен, соответствующий вектору ошибки делится на g(x) без остатка, то есть если вектор ошибки совпадет с разрешенным кодовым словом.
– Конец работы –
Используемые теги: курсу, Теория, информационных, процессов, систем0.081
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: По курсу Теория информационных процессов и систем
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов