рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Информатика
- /
- ИНФОРМАТИКА
Реферат Курсовая Конспект
ИНФОРМАТИКА
ИНФОРМАТИКА - раздел Информатика, ...
 МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

«МАТИ» Российский Государственный Технологический Университет им. К.Э. Циолковского
И Н Ф О Р М А Т И К А
ОглавлениеГлава 1. Базовые понятия информатики
1.1 Информатика
Термин «информатика» (франц. Informatique) происходит от французских слов information (информация, латинское – information, что означает «сведения, разъяснения , изложение») и automatique (автоматика) и означает «информационная автоматика» (англоязычный вариант: Computer science – компьютерная наука).
Информатикой называют науку, изучающую структуру и свойства информации, а также занимающуюся вопросами сбора, хранения, поиска, передачи, преобразования, распространения и использования информации.
Информатика представляет собой неразрывное единство трех составных частей: теории передачи и преобразования информации, алгоритмических средств обработки информации и вычислительных средств.
В 1978 г. международный научный конгресс официально закрепил за понятием «информатика» области, связанные с разработкой, созданием, использованием и материально-техническим обслуживанием систем обработки информации, включая компьютеры и их программное обеспечение, а также организационные, коммерческие, административные и социально-политические аспекты компьютеризации – массового внедрения компьютерной техники во все области жизни людей.
1.2 Информация
Информацией в простейшем смысле называют сведения об объектах, процессах и явлениях окружающего нас мира. Термин «информация» имеет много определений. В широком смысле информация – отражение реального мира. В обиходе информацией называют любые данные или сведения, которые кого-либо интересуют. Сведения могут поступать к человеку из различных источников: книги, газеты, картины, музыкальные произведения, в процессе общения и т.д.
Информация – категория нематериальная, следовательно, для существования и распространения в материальном мире она должна быть связана с какой – либо материальной основой. Без материальной основы информация не может проявиться, передаваться и сохраняться. Определим материальный носитель как материальный объект или среду, которые служат для представления или передачи информации. Например, бумага, лазерный диск, воздух – материальные носители информации. При этом хранение информации связано с некоторой характеристикой носителя, которая не меняется с течением времени, а передача информации связана с характеристикой, которая изменяется с течением времени. Однако не с любым процессом можно связать информацию. Возможны процессы с неизменными в течение времени характеристиками (стационарные). Стационарные процессы информацию не переносят, например, постоянный электрический ток, равномерный гул. Эти процессы содержат лишь информацию о своём функционировании. Для передачи необходим нестационарный процесс, т.е. процесс, характеристики которого могут изменяться, при этом информация связывается не с существованием процесса, а именно с изменением какой – либо его характеристики. Будем называть изменение характеристики носителя, которое используется для представления информации – сигналом, а значение этой характеристики, отнесённое к некоторой шкале измерений параметром сигнала.
Рассмотрим пример:
Пусть способом передачи является звук, в том случае процесс – это звуковые волны, параметры сигнала – высота и громкость звука.
Последовательность сигналов будем называть сообщением.
Различают источники информации, средства ее передачи и приемники информации.
Субъект или объект, порождающий информацию и представляющий её в виде сообщения, является источником информации. Субъект или объект, принимающий сообщение и способный правильно его интерпретировать является преемником информации.
При этом необходимо иметь в виду, что при передаче информации по каналам связи возможны помехи, которые вызывают искажение и потерю информации.
Свойства информации.
- Важность (ценность, полезность); - Достоверность (истинность, правильность): - полноту;Формула Хартли
I=log2N.
Рассмотрим пример: допустим, нужно угадать число из набора целых чисел от нуля до 63. В соответствии с формулой Хартли количество информации в… Формула Хартли определяет длину двоичного слова (I), которое требуется для… Такой подход для определения количества информации назвали вероятностным. Рассмотрим с этой точки зрения формулу…I=log2N=log2(1/p)=-log2p.
Следует учесть, что не все события могут быть равновероятны. Для такого рода задач американский ученый Клод Шеннон в 1948г. предложил формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе.
Формула Шеннона.
где рi – вероятность того, что именно i-е сообщение выделено в наборе из N сообщений. К. Шеннон назвал полученную величину энтропией.Обозначают, как правило, буквой… Энтропия обладает следующими свойствами: энтропия всегда неотрицательна, так как значения вероятностей…Источник – кодирующее устройство – кодер канала – канал связи – декодер канала – декодирующее устройство – приёмник.
Если избыточность источника сообщений мала и помехи в канале связи практически отсутствуют, то введение как кодера источника, так и кодера канала… 1.6. Передача информации Современные вычислительные средства (персональные ЭВМ, микро-, мини- и макси ЭВМ) часто используются в составе…Глава 2. Общие принципы организации и работы компьютеров
2.1 Принцип построения компьютера, структура компьютера
При рассмотрении вычислительных устройств(компьютеров) принято различать их архитектуру и структуру.
Структура компьютера – это совокупность его функциональных элементов и связей между ними. Элементами могут быть самые различные устройства – от основных логических узлов компьютера до простейших схем. Структура компьютера графически представляется в виде структурных схем, с помощью которых можно дать описание компьютера на любом уровне детализации.
В основу построения подавляющего большинства компьютеров положены общие принципы сформулированные в 1945г. Американским учёным Джоном фон Нейманом.
Принципы фон Неймана
По сути, Нейману удалось обобщить научные разработки и открытия многих других ученых и сформулировать на их основе принципиально новое. Принцип программного управления: программа состоит из набора команд,… Принцип однородности памяти:программы и данные хранятся в одной и той же памяти .ЭВМ — программно-управляемый цифровой автомат.
· ЭВМ управляется специальной программой, которая может либо вводиться в ЭВМ, либо храниться в её памяти. Следует подчеркнуть очень важные функции… Далее более подробно охарактеризуем каждый функциональный блок ЭВМ. · Память (запоминающее устройство) — функциональная часть ЭВМ предназначенная для хранения входной информации,…Архитектура с параллельными процессорами.
Архитектура с параллельными процессорами предполагает наличие нескольких АЛУ, которые работают под управлением одного УУ.
Многомашинные вычислительные системы.
Многомашинные вычислительные системы состоят из нескольких процессоров, не имеющих общей оперативной памяти. Каждый компьютер в многомашинной вычислительной системе имеет собственную (локальную) память и классическую архитектуру.
Многопроцессорная архитектура.
Многопроцессорная архитектура предусматривает наличие в компьютере нескольких процессоров, что позволяет параллельно обрабатывать несколько потоков данных и несколько команд.
Открытая архитектура.
- наличие общей информационной шины, к которой подключаются дополнительные устройства через разъёмы расширения; - модульное построение компьютера; - совместимость всех новых устройств и программных средств с предыдущими версиями.Краткая история развития ЭВМ
1614 г. -шотландец Джон Непер изобрёл логарифмы. Вскоре после этого Р. Биссакар создал логарифмическую линейку. 1642 г. -французский ученый Блез Паскаль приступил к созданию арифметической… 1804 г. -французский инженер Жаккар изобрёл перфокарты для управления автоматическим ткацким станком, способным…Первое поколение
Электронная лампа Компьютер "Эниак".Второе поколение
БЭСМ—6. ТранзисторТретье поколение
Интегральная схемаЧетвертое поколение
Наиболее важный в концептуальном отношении критерий, по которому эти компьютеры можно отделить от машин третьего поколения, состоит в том, что… В аппаратурном отношении для них характерно широкое использование интегральных… C точки зрения структуры машины этого поколения представляют собой многопроцессорные и многомашинные комплексы,…Глава 3. Алгоритмы. Алгоритмизация
3.1 Абстрактные автоматы и понятие алгоритма
Классические примеры абстрактных автоматов -— машина Тьюринга или алгоритмическая система Поста( Пост в отличие от Тьюринга не пользовался термином машина). Чтобы подчеркнуть единство подходов обоих авторов будем употреблять термин «машина». Машина Поста состоит из бесконечной ленты, разделенной на отдельные секции (ячейки), в которые можно либо заносить метку, либо считывать метку с помощью записывающей или считывающей головки (рис. 3.1). Лента (или головка) может передвигаться в левую или правую стороны на один шаг в зависимости от команды. Лента всегда останавливается так, чтобы напротив головки находилась секция (ячейка). Команды абстрактного автомата обычно включают в себя одно из следующих действий (на примере машины Поста); движение головки вправо, движение головки влево, запись метки, стирание метки, передача управления, остановка (стоп).
Каждая команда имеет свой номер i. Стрелка указывает направление движения. Второе число j, стоящее в конце команды, называется отсылкой.
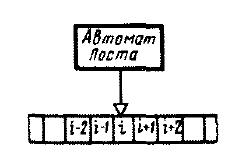
Рис. 3.1.
У команды передачи управления могут быть две отсылки. Поэтому программа абстрактного автомата должна обладать двумя свойствами:
- на первом месте в списке всегда стоит команда с номером 1, на втором месте — с номером 2 и т. д.;
- отсылка любой из команд всегда находится в списке команд программы.
После передвижения ленты влево или вправо головка считывает состояние секции (пустая или записана метка). Информация о том, какие секции пусты, а какие отмечены, образует состояние ленты или состояние автомата. Таким образом, обладая указанным выше набором команд, автомат может осуществлять определенные действия, которые будут задаваться программой. Программой абстрактного автомата будем называть конечный непустой список команд.
Для «работы» абстрактного автомата необходимо задать программу и начальное состояние, т. е, положение головки и состояние ячеек ленты. После этого автомат приступает к выполнению команды номер 1. Все секции (ячейки) ленты нумеруются в определенном порядке. Порядок нумерации ячеек может совпадать с порядком, в котором расположены натуральные целые числа.
Каждая команда выполняется за один шаг, после чего начинается выполнение команды, номер которой указан в отсылке. Если эта команда имеет две отсылки, то команда с номером верхней отсылки выполняется, если под головкой находится пустая ячейка. Если же под головкой находится ячейка с меткой, то выполняется команда с номером нижней отсылки. Выполнение команды передачи управления не изменяет состояния автомата (ни одна из меток не уничтожается и не ставится, и лента остается неподвижной). При запуске автомата может возникнуть одна из следующих ситуаций:
автомат дошел до выполнения невыполнимой команды (запись метки в занятую ячейку, стирание метки в пустой ячейке); выполнение программы прекращается, автомат останавливается (назовем это состояние поломкой автомата), происходит безрезультатная остановка;
автомат дошел до команды стоп, программа считается выполненной, происходит результатная остановка;
автомат не доходит ни до результатной, ни до безрезультатной остановки, происходит бесконечная работа (автомат «завис»).
На таких элементарных автоматах, как машина Поста или машина Тьюринга, можно проводить различные действия над числами. Для этого необходимо представлять числа в абстрактном автомате.
Назовем последовательность секций (ячеек), содержащих метку, массивом, а число секций в нем — длиной массива. Условимся число n представлять на ленте массивом длины n + 1. Тогда этот массив будем называть автоматным изображением числа. Например, числа 6, 3 и 2 представлены соответственно на рис. 3.2. автоматными изображениями.

Рис. 3.2.автоматные изображения чисел
Представим себе, что на машине Поста надо прибавить 1 к любому числу.
Для этого требуется написать программу для машины Поста, обладающую следующим свойством: для любого числа n, записанного на ленте, программа должна дать результатную остановку с записью числа n+1 в произвольном месте ленты.
Программа должна выглядеть следующим образом:

В качестве начального состояния может быть выбрано любое состояние, при котором головка находится на одной из отмеченных ячеек ленты(т. е. над набором числа). Если же головка будет находиться в произвольном месте ленты, то программа усложнится. С помощью абстрактного автомата можно реализовать и другие преобразования числовой информации.
Можно составить программы для сложения, умножения, деления чисел. Есть ли ограничения на вычисления, производимые на машине Поста? Ответ на этот вопрос был сформулирован самим Э. Постом в следующем виде: «Задача па составление программы, приводящей от исходного данного к результирующему числу, тогда и только тогда имеет решение, когда имеется какой-нибудь общий способ, позволяющий по произвольному и одному данному выписать результирующее число».
Формулировка постулата Поста подводит к понятию алгоритма.
Английский математик А. М. Тьюринг в работе «О вычислимых числах с приложением
к проблеме разрешения» и американский математик Э, X, Пост в работе «Финитные комбинаторные процессы» почти одновременно в 1936 г. дали уточнения понятия «алгоритм» на примере гипотетической машины с бесконечной лентой. Машина Тьюринга отличается от
машины Поста тем, что ячейки заполняются не просто меткой, а символами из заданного множества, у машины Тьюринга есть логическое устройство.
Исторически термин «алгоритм» произошёл от фамилии узбекского математика IX века Мухаммада ибн Муса ал – Хорезми, который впервые сформулировал правила четырёх арифметических действий. Поначалу именно эти правила назывались алгоритмами, но затем термин получил дальнейшее развитие в первую очередь в математике.
Существует много определений термина «алгоритм». Например, по определению акад. Л, Н. Колмогорова, алгоритм или алгорифм — это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
В инженерной практике часто используется следующее определение: алгоритм — конечная совокупность точно сформулированных правил решения какой-то задачи .
3.2 Формы записи алгоритмов.
Словесная форма записи алгоритма.
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задаётся в произвольном изложении на естественном языке.
Например, алгоритм нахождения наибольшего общего делителя( алгоритм Евклида) двух натуральных чисел можно записать следующим образом:
1) задать два числа;
2) если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
3) определить большее из чисел;
4) заменить большее из чисел разностью большего и меньшего из чисел;
5) повторить алгоритм с шага 2.
По указаниям этого алгоритма можно найти наибольший общий делитель для любой пары целых чисел.
Словесный способ не имеет широкого распространения, так как такие описания не строго формализуемы, допускают неоднозначность толкования отдельных предписаний.
Графический способ записи алгоритмов.
Псевдокод.
Псевдокод занимает промежуточное место между естественными и формальными языками. В псевдокоде не приняты строгие синтаксические правила для записи команд,… Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи…Математическая форма задания алгоритма.
Пример алгебраической формы алгоритма – любая математическая формула для нахождения какой – то величины.
3.3 Характеристики алгоритма
Характеристиками алгоритма являются:
- детерминированность, определяющая однозначность результата решения задачи при заданных исходных данных;
- дискретность определяемого алгоритмом процесса, означающая разделение алгоритма на отдельные элементарные шаги, причём выполнение очередного шага возможно только после завершения всех операций на предыдущем шаге;
- массовость, позволяющая применять один и тот же алгоритм для некоторого множества однотипных задач;
- элементарность шагов: закон получения последующей системы величин из предыдущей должен быть простым и локальным;
Эти характеристики не дают точного описания алгоритма, а лишь объясняют смысл этого термина в математике.
Детерминированный алгоритм — алгоритм, имеющий место при четкой и ясной системе правил и указаний и однозначных действиях.
Случайный алгоритм — алгоритм, предусматривающий возможность случайного выбора тех или иных правил.
Алгоритм должен обеспечивать получение результата через конечное число шагов для любой задачи определенного класса. В противном случае задача неразрешима. Нахождение алгоритма решения задачи называется алгоритмизацией.
Процесс выполнения алгоритма называется алгоритмическим процессом. Для некоторых исходных данных он заканчивается получением искомого результата после конечного числа шагов. Однако возможны случаи, когда искомый результат не достигается или безрезультатно обрывается. Тогда говорят, что к таким исходным данным алгоритм неприменим.
Процесс решения задачи на ЭВМ прежде всего должен быть выражен каким-то алгоритмом. Разработка алгоритмов решения задач — задача программиста, а разработка алгоритмов функционирования цифрового автомата для решения поставленных задач — задача инженера-разработчика.
3.4 Исполнители алгоритма
Исполнитель алгоритма – это субъект или устройство, способные правильно интерпретировать описание алгоритма и выполнить содержащийся в нем перечень действий.
Указания по выполнению действий для каждого исполнителя формулируются посредством некоторого языка, включающего набор служебных слов, обозначающих действия (команды), а также синтаксические правила их объединения. Совокупность допустимых команд образует систему команд исполнителя.
Исполнителя характеризуют:
• среда;
• элементарные действия;
• система команд;
• отказы.
Среда ( или обстановка) — это " место обитания" исполнителя.
Система команд. Каждый исполнитель может выполнять команды только из
некотоpого стpого заданного списка — системы команд исполнителя. Для каждой
команды должны быть заданы условия пpименимости (в каких состояниях сpеды может
быть выполнена команда) и описаны pезультаты выполнения команды.
После вызова команды исполнитель совеpшает соответствующее элементаpное
Действие.
Отказы исполнителя возникают, если команда вызывается пpи недопустимом для
нее состоянии сpеды.
Обычно исполнитель ничего не знает о цели алгоpитма. Он выполняет все полученные
команды, не задавая вопросов "почему" и "зачем".
В информатике универсальным исполнителем алгоритмов является компьютер.
Глава 4. Арифметические основы ЭВМ.
4.1 Системы счисления
Информация, обрабатывая ЭВМ и находящаяся внутри вычислительной машины, всегда представлена в виде чисел, записанных в той или иной системе счисления. Вопрос о выборе системы счисления для цифрового автомата - один из важнейших вопросов проектирования как алгоритмов функционирования отдельных устройств, так и расчёта технических характеристик автомата.
Можно считать, что любое число имеет значение (содержание) и форму представления( т. е. запись числа). Значение числа задает порядок расположения чисел на числовой оси, или другими словами его отношение к значениям других чисел («больше», «меньше», «равно»). Форма представления определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа не зависит от способа его представления. Это означает также, что число с одним и тем же значением может быть записано по-разному, т.е. отсутствует взаимно однозначное соответствие между представлением числа и его значением. Например, число пять в римской системе счисления представляется как символ «V», в двоичной системе счисления как набор символов – цифр «101», в десятичной системе счисления как символ – цифра «5» и т.д., этот ряд можно продолжать бесконечно. В связи с этим возникают вопросы, во-первых, о формах представления чисел, и, во-вторых, о возможности и способах перехода от одной формы к другой.
Способ представления числа определяется системой счисления.
Система счисления – совокупность приёмов и правил для записи числа символами(цифровыми знаками).
Любая предназначенная для практического применения система счисления должна обеспечивать единственность представления числа и простоту оперирования числами.
Способы записи чисел можно объединить в две группы: непозиционные и позиционные. В свою очередь позиционные системы счисления подразделяются на традиционные системы счисления и нетрадиционные системы счисления.
Непозиционные системы счисления.
Системы счисления, в которых каждой цифре соответствует величина, независящая от местоположения этой цифры в записи числа, называются непозиционными.
Принципы построения таких систем не сложны. Для их образования используют в основном операции сложения и вычитания.
К непозиционным системам счисления можно отнести унарную систему. Система с одним символом(палочкой) встречалась у многих народов.
Наиболее известная непозиционная система счисления - римская. В римской системе счисления для изображения чисел используются символы I, V, X, L(50), C(100), D(500),М(1000). Десятичное число 27 представляется следующим образом: XXVII=10+10+5+1+1. В непозиционных системах счисления не представляются дробные и отрицательные числа. Арифметические операции выполнять в непозиционной системе счисления очень сложно, так как отсутствуют правила для выполнения действий.
Позиционные системы счисления.
Системы счисления, в которых вклад каждой цифры в величину числа зависит от ее положения (позиции) в последовательности цифр, изображающей число, называются позиционными. Для позиционных систем счисления характерным и определяющим является наличие основания системы, которое показывает, во-первых, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию(влево или вправо) и, во-вторых, какое количество различных цифр входит в ограниченный набор, называемый алфавитом системы, используемый для записи любого числа.
Под алфавитом позиционной системы счисления понимают совокупность различных цифр (символов), используемых для записи чисел.
Для записи чисел в конкретной системе счисления используется некоторый конечный алфавит, состоящий из цифр - символов.
При этом основанием традиционной системы счисления может быть любое натуральное число р³2. Наименование системы счисления соответствует ее основанию. Количество цифр, используемых в р-ичных системах счислениях для записи алфавита равно основанию системы счисления Например, алфавит двоичной системы счисления состоит из двух цифр 0 и 1. Алфавит двенадцатеричной системы счисления состоит из 12 цифр-символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Традиционных цифр-символов для записи алфавита этой системы счисления оказалось недостаточно, поэтому были введены в качестве цифр заглавные буквы латинского алфавита.
В теории чисел рассматриваются системы счисления, основаниями которых могут быть любые натуральные числа>1, а также доказывается, что в любой позиционной системе счисления можно записать любое число и притом единственным образом.
Запишем алфавиты систем счисления, используемых в информатике:
- двоичная система счисления 0,1;
- четверичная система счисления 0,1,2,3;
- восьмеричная система счисления 0,1,2,3,4,5,6,7;
- шестнадцатеричная система счисления 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F.
Любое число А в позиционной системе счисления можно представить суммой произведений целых однозначных коэффициентов ai, взятых из алфавита системы на последовательные целые степени основания p (так называемая развернутая форма записи числа):
 , (4.1)
, (4.1)
где m — количество цифр в целой части числа или Аq=
 ×qk, для целой части числа и Аq=
×qk, для целой части числа и Аq=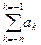 ×qk (4.2)
×qk (4.2)
где ак-любая цифра из алфавита системы с основанием равным q, m, n-число позиций соответственно для целой и дробной частей числа.
Степенной ряд для целой и дробной частей числа можно представить эквивалентными выражениями по схеме Горнера:
для целой части: Аq= ak×qk=(…((am-1q+am-2q)q+am-3)q+…+a1)q+a0; (4.3)
ak×qk=(…((am-1q+am-2q)q+am-3)q+…+a1)q+a0; (4.3)
для дробной части Aq=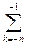 akqk=q-1(a-1+q-1(a-2+…q-1 (a-k+1+a-kq-1)…)). (4.4)
akqk=q-1(a-1+q-1(a-2+…q-1 (a-k+1+a-kq-1)…)). (4.4)
4.2 Перевод чисел из одной системы счисления в другую.
1) Перевод целых чисел из одной системы счисления в другую.
Целое число в системе счисления q может быть представлено эквивалентным числом в системе счисления р по формуле (1.3)
Аq=Ар=(…((bm-1p+bm-2p)q+bm-3)p+…+b1)p+b0. (4.5)
Задача перевода числа из одной системы счисления(q) в другую систему счисления (р) заключается в отыскании значений цифр bk числа в новой системе счисления.
Разделив обе части равенства (4.5) на основание новой системы р, выраженное цифрами системы счисления q, получим:
 (4.6)
(4.6)
или Аq=Ap=(Aq)1+b0, где (Аq)1 – целое частное, b0 – остаток, являющийся первой младшей цифрой числа в новой системе счисления, остаток выражен цифрами исходной системы счисления.
При следующем делении частного на основание системы счисления р будут получены новое частное и новый остаток: (Аq)1=(Aq)2+b1, где b1 – вторая младшая цифра числа. Продолжая деление целых целых частных до нулевого значения частного, находим все цифры числа в новой системе счисления.
Правило перевода целого числа из одной системы счисления в другую.
1) последовательно делить данное число и получаемые целые частные на основание новой системы счисления , выраженные цифрами исходной системы, до тех пор, пока частное не станет равным нулю.
2)Полученные остатки, являющиеся цифрами числа в новой системе счисления, выразить цифрами алфавита этой системы счисления.
3)Записать число в новой системе, начиная с последнего остатка.
2) Перевод дробных чисел.
Рассуждая по аналогии с переводом для целых чисел, но используя операцию умножения, сформулируем правило перевода дробных чисел.
Правило перевода дробных чисел из одной системы счисления в другую.
1) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы , выраженное цифрами исходной системы, до тех пор, пока либо дробная часть произведения не станет равной нулю, либо не появится период, либо не будет достигнуто заданное количество разрядов искомой дроби.
2) Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, выразить цифрами алфавита этой системы.
3) Записать дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
4.3 Перевод из 10-ной системы счисления в р-ную.
1.) Используем изложенный способ перевода числа из одной системы счисления в другую при р=10 и q=2.
Пусть десятичное число равно 13. Чтобы перевести его в двоичную систему счисления необходимо проделать следующие арифметические операции:
  1 1
| ||||||
Число 13 делим на 2, полученный остаток будет младшим разрядом искомого двоичного числа.
Каждое очередное частное делится на 2 до тех пор, пока частное от деления не станет не станет равным 0.
Последнее частное является старшим разрядом двоичного числа. Запишем полученное последнее частное и все остатки по порядку справа—налево — 1101, это и есть число 13 в двоичной системе счисления, 1310=11012.
Сущность вычислений заключается в многократном делении целых чисел на 2.
Рассмотрим перевод дробного десятичного числа в двоичную форму. Для этого мы должны проделать арифметическую операцию умножения до первого полученного нуля в дробной части, либо до определенного количества значащих цифр.
Поясним на примерах.
1) переведем число 0,5 (десятичное) в двоичную систему счисления. Для наглядности будем приводить умножение «столбиком».
 0 0
| |
2) 0,7510 переводим в двоичную систему счисления.
 |
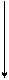 0 0
| 75 2 |
| 50 2 | |
Выписываем разряды «сверху—вниз».
3) 0,3310 переводим в двоичную систему.
 0 0
| 33 2 |
| 66 2 | |
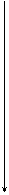 1 1
| 32 2 |
| 64 2 | |
| 28 2 | |
| 56 2 | |
| 12 2 | |
| 24 2 | |
| 48 2 | |
| 96 2 | |
| 92 ... |
4) Перевести 10,2510 в двоичную систему счисления.
| 0, | 25 2 |
| 50 2 | |
| 0 |
10,2510=1010,012.
2.) Выполнить перевод числа из одной системы счисления в другую можно подбором соответствующих показателей основания системы счисления и коэффициентов при этих степенях, т. е. записать развернутую форму числа, но уже в другой системе счисления. Наиболее легко этот способ реализуется для двоичной системы счисления, так как коэффициенты при степенях могут принимать значения либо 0, либо 1. Например, переведем число 123 в двоичную систему счисления подбором показателей степеней и коэффициентов при них. Составим таблицу степеней числа 2 и посмотрим, какие из этих степеней могут в сумме составить число 123.
Таблица степеней числа 2.
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 210 |
123=64+32+16+8+2+1=1×26+1×25+1×24+1×23+0×22+1×21+1×20=11110112.
Рассмотрим перевод целых и дробных чисел из десятичной системы счисления в восьмеричную систему счисления.
В восьмеричной системе счисления для представления числа используются цифры от 0 до 7. Правила перевода естественно остаются прежними.
Пример
21,2510 переведем в восьмеричную систему счисления.
| 2110=258 0,2510=0,28 21,2510=25,28 |
| 25 8 | |
При переводе из десятичной системы счисления в шестнадцатеричную , необходимо помнить о том, что количество символов алфавита шестнадцатеричной системы счисления превышает количество символов алфавита десятичной системы счисления и двузначные числа 11,12,13,14,15 десятичной системы счисления являются однозначными в системе счисления по основанию 16.
В шестнадцатеричной системе счисления для записи любого числа необходимо 16 цифр, для изображения недостающих цифр используются заглавные буквы латинского алфавита.
Алфавит шестнадцатеричной системы счисления:
| A | B | C | D | E | F | ||||||||||
Пример.
Перевести десятичное число 142,25 в шестнадцатеричную систему счисления.
| 14210=8E8 0,2510=0,416 142,2510=8E,416 |
| (E) |
| 0, | 25 16 |
4.4 Перевод чисел из р-ичной системы счисления в десятичную.
Для того, чтобы перевести р-ичное число в десятичную систему счисления, запишем его в развернутой форме, а затем, выполнив необходимые вычисления, получим соответствующее десятичное число.
Пример 1.
Перевести из восьмеричной системы счисления в десятичную следующие числа:
-13.48; 27.518; 14.28; 127.038
Запишем развернутую форму записи числа в восьмеричной системе счисления, основание системы счисления108, выразим цифрой десятичной системы счисления 108=810
Выполним перевод для первого числа:
-13.48= -(138+0.48)
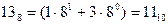
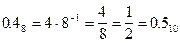
-13.48= -11.510.
Остальные примеры решите самостоятельно.
Пример 2.
Перевести следующие числа: 1110011.012, -456.078, 1АС.1516.
1110011.01=1×26+1×25+1×24+0×23+0×22+1×21+1×20+
0×2-1=64+32+16+2+1+0.25=115.25; остальные примеры выполните самостоятельно.
4.5 Системы счисления с основаниями, являющимися степенью 2.
При решении примеров по переводу чисел из одной системы счисления в другую (при этом обе системы имеют в качестве основания степени числа 2) может понадобиться таблица переводов.
Таблица переводов.
| Система счисления с основанием 10 | Система счисления с основанием 2 | Система счисления с основанием 8 | Система счисления с основанием 16 |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Двоично-восьмеричная система счисления.
1001101.10112 Для того, чтобы представить исходное число в восьмеричной системе счисления… 001 001 101.101 100 =115.548Двоично-шестнадцатеричная система счисления.
Запишем некоторое число в двоичной системе счисления:
1001101.10112
Для того, чтобы представить исходное число в шестнадцатеричной системе счисления разобьем его на тетрады. Целую часть от десятичной точки влево, добавляя впереди стоящие нули, если не хватает цифр, и дробную часть вправо от десятичной точки, добавляя сзади стоящие нули, если не хватает разряда.
D.B
 |  | 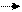 |
Каждая двоичная тетрада заменяется соответствующим шестнадцатеричным числом.
Обратный перевод из восьмеричной или шестнадцатеричной системы счисления в двоичную систему счисления.
При выполнении перевода следует помнить о том, что для восьмеричной системы счисления каждая цифра заменяется двоичной триадой, а для шестнадцатеричной системы счисления каждая цифра заменяется двоичной тетрадой.
Пример 1.
Перевести восьмеричное число 4501 в двоичную систему счисления.
45018=100 101 000 0012.
Пример 2.
Перевести шестнадцатеричное число 4А9С05 в двоичную систему счисления.
4А9С0516=100 1010 1001 1100 0000 01012.
Задачи.
- Перевести обыкновенную дробь
 , представленную в десятичной системе счисления , в восьмеричную систему счисления.
, представленную в десятичной системе счисления , в восьмеричную систему счисления.
Решение.
Применим правило перевода дробных чисел из одной системы счисления в другую.
 ×8=
×8=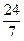 =3
=3 целая часть результата является первым разрядом искомой дроби, дробная часть результата равна
целая часть результата является первым разрядом искомой дроби, дробная часть результата равна  , следовательно мы вышли на период. Первый найденный разряд выражен в алфавите восьмеричной системы счисления.
, следовательно мы вышли на период. Первый найденный разряд выражен в алфавите восьмеричной системы счисления.
Ответ:  =0.(3)8.
=0.(3)8.
- Перевести обыкновенную дробь
 представленную в десятичной системе счисления в шестнадцатеричную систему счисления.
представленную в десятичной системе счисления в шестнадцатеричную систему счисления.
Решение.
 ×16=
×16=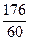 =2
=2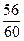
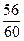 ×16=
×16=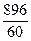 =14
=14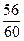 .
.
Процесс умножения прекращается, так как найден период результирующей дроби. Теперь необходимо полученные целые числа выразить в алфавите шестнадцатеричной системы счисления. Первый разряд искомой дроби выражен в алфавите шестнадцатеричной системы счисления, выразим второй разряд искомой дроби в алфавите шестнадцатеричной системы счисления: 1410=Е16.
Ответ:  10=0.2(Е)16.
10=0.2(Е)16.
- Периодическую дробь 0.(23), представленную в десятичной системе счисления, перевести троичную систему счисления.
Решение.
Заменим периодическую дробь0.(23)10 обыкновенной дробью.
Для этого проделаем следующие действия:
1) Обозначим исходную дробь через х, тогда
х = 0.(23) (а)
2) Умножим левую и правую части уравнения (а) на 102 (показатель степени равен количеству нулей в периоде), получаем
100х = 23.(23) (б)
3) Вычтем из уравнения (б) уравнение (а), получаем
100х-х = 23 (в)
4) Найдем из уравнения (в) х:
х = 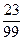 .
.
Применяя правило перевода дробей, переведем полученную обыкновенную дробь в троичную систему счисления.
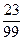 ×3=
×3= =0
=0
 ×3=
×3= =2
=2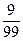
Глава 5. Представление данных в памяти ЭВМ.
5.1 Проблемы представления данных
Для физического представления чисел необходимы элементы, способные находиться в одном из нескольких устойчивых состояний.
Если для построения ЭВМ выбрана десятичная система счисления, то таких состояний должно быть десять. Для восьмеричной системы счисления таких состояний должно быть 8, для шестнадцатеричной — 16 и т.д. Число состояний всегда должно быть равно основанию системы счисления.
Естественно, такое количество состояний вызывает трудности при их реализации.
В середине сороковых годов прошлого столетия группа математиков, в которую входил и фон Нейман, предложила использовать для представления информации в ЭВМ двоичную систему счисления.
Для двоичной системы счисления устойчивых состояний должно быть два (грубо говоря — выключатель включен (этому состоянию логически соответствует 1) и выключатель выключен (этому состоянию логически соответствует 0).
Совершенно очевидно, что наиболее простыми с точки зрения технической реализации являются так называемые двухпозиционные элементы, способные находиться в одном из двух устойчивых состояний, например: электромагнитное реле замкнуто или разомкнуто, ферромагнитная поверхность намагничена или размагничена и т.д.
Простота технической реализации двухпозиционных элементов обеспечила наибольшее распространение в ЭВМ двоичной системы счисления.
Кроме того, в информатике используется также восьмеричная и шестнадцатеричная системы счисления. Основания этих систем соответствуют целым степеням 2, поэтому для них исключительно просты правила перевода в двоичную систему счисления и наоборот.
Любая информация представляется в ЭВМ в виде двоичных кодов. Отдельные элементы двоичного кода, принимающие значение 0 или 1 называются разрядами или битами.
| n |
Хранит информацию блок машины называемой памятью. Условно блок памяти изобразим прямоугольником. Память делится на байты. Наименьшей неделимой единицей информации, которой можно присвоить адрес является байт( в современных ЭВМ под байт отводят 8 разрядов). Номера начинаются с нуля и заканчиваются некоторым числом «n». Значение n зависит от типа ЭВМ.
Память хранит:
n данные (так называемая область данных)
n программы (область программ)
n служебную информацию (она называется системной, и область также называется системной, таких областей в памяти две).
Память «начинается» системной областью и «заканчивается» системной областью.
Итак, память подразделяется на ячейки(разрядные сетки) обратиться к которым можно по их адресам.
Каждый байт памяти подразделяется на разряды или биты.
Условно разрядную сетку можно изобразить в виде узкого прямоугольника с делениями для разрядов (битов).
| M | |||||||
| .............. |
Разрядная сетка
Каждому разряду (биту) соответствует один физический элемент. Логически это 1, либо 0.
Представление числовой информации в памяти ЭВМ неразрывно связано с таким понятием современных проблемно – ориентированных языков, как тип данных. Современные языки достаточно строго отслеживают тип переменных, которые используются в программе. Тип переменной определяет возможный набор значений данной переменной, размер её внутреннего представления и множество операций, которые могут выполняться над переменной. Для числовых значений существенным моментом является диапазон допустимых значений.
Понятие типа данных носит двойственный характер. С точки зрения размерности микропроцессор аппаратно поддерживает следующие основные типы данных:
Байт — восемь последовательно расположенных битов, пронумерованных от 0 до 7, при этом бит 0 является самым младшим значащим битом.
Двойной байт (слово в 16/32-битной архитектуре) — последовательность из двух байт, имеющих последовательные адреса. Размер слова — 16 бит; биты в слове нумеруются от 0 до 15. Байт, содержащий нулевой бит, называется младшим байтом, а байт, содержащий 15‑й бит — старшим байтом. Микропроцессоры Intel имеют важную особенность — младший байт всегда хранится по меньшему адресу. Адресом двойного байта считается адрес его младшего байта. Адрес старшего байта может быть использован для доступа к старшей половине двойного байта.
Полуслово — последовательность из четырех байт (32 бита), расположенных по последовательным адресам. Нумерация этих бит производится от 0 до 31. Двойной байт, содержащий нулевой бит, называется младшим двойным байтом, а двойной байт, содержащий 31-й бит — старшим двойным байтом. Младший двойной байт хранится по меньшему адресу. Адресом полуслова считается адрес его младшего байта. Адрес старшего двойного байта может быть использован для доступа к старшей половине полуслова.
Слово (тип, резрядность которого соответствует разрядности архитектуры) — последовательность из восьми байт, имеющих последовательные адреса. Размер слова — 64 бита; биты в слове нумеруются от 0 до 63. Полуслово, содержащее нулевой бит, называется младшим полусловом, а полуслово, содержащее 63-й бит — старшим полусловом. Микропроцессоры Intel имеют важную особенность — младшее полуслово всегда хранится по меньшему адресу. Адресом слова считается адрес его младшего байта. Адрес старшего полуслова может быть использован для доступа к старшей половине слова.
Двойное слово — последовательность из шестнадцати байт (128 бита), расположенных по последовательным адресам. Нумерация этих бит производится от 0 до 127. Слово, содержащее нулевой бит, называется младшим словом, а слово, содержащее 127-й бит, — старшим словом. Младшее слово хранится по меньшему адресу. Адресом двойного слова считается адрес его младшего слова. Адрес старшего слова может быть использован для доступа к старшей половине двойного слова.
Кроме трактовки типов данных с точки зрения их разрядности, микропроцессор на уровне команд поддерживает логическую интерпретацию этих типов.
Целый тип без знака — двоичное значение без знака, размером 8, 16, 32, 64 или 128бит.
- байт — от 0 до 255;
- два байта — от 0 до 65 535;
- полуслово — от 0 до 232–1;
- слово — от 0 до 264–1;
- двойное слово — от 0 до 2128–1.
Целый тип со знаком — двоичное значение со знаком, размером 8, 16, 32, 64 или 128бит. Знак в этом двоичном числе содержится в старшем бите.
Числовые диапазоны для этого типа данных следующие:
- 8-разрядное целое — от -128 до +127;
- 16-разрядное целое — от -32 768 до +32 767;
- 32-разрядное целое — от -231 до +231 – 1;
- 64-разрядное целое — от -263 до +263 – 1;
- 128-разрядное целое — от -2127 до +2127 – 1.
Действительный тип кодирует действительное число в экспоненциальной форме:
Закодированное число вычисляется по формуле:
N = мантиса · 2 порядок;
- 32-разрядное действительное — от 3,4·10-38 до 3,4·1038;
- 64-разрядное действительное — от 1,7·10-308 до 1,7·10308;
- 80-разрядное действительное — от 3,4·10-4932 до 1,1·104932.
Следует отметить, что помимо разрядности, определённой типом процессора необходимо учитывать и язык программирования ( конкретно возможности компилятора). Например, язык программирования Турбо Паскаль поддерживает тип данных real, для этого типа данных отведено 48 разрядов.
Повторим, что минимальной адресуемой единицей информации, обрабатываемой в ЭВМ, является байт. Байт состоит из восьми двоичных разрядов.
Рассмотрим подробно представление чисел в памяти ЭВМ.
5.2 Формы представления чисел в ЭВМ.
Для представления чисел в ЭВМ применяются две различные формы: с фиксированной точкой (запятой) - для целых чисел и с плавающей точкой (запятой) для действительных чисел.
Целые числа могут быть представлены со знаком и без знака.
Возьмем разрядную сетку из 8 бит (т.е. байт) и попробуем разобраться, как представляются целые числа без знака. Самое маленькое число, которое можно поместить в один байт без знака — это ноль.
Число 0 без знака.
Самое большое число, которое можно представить в одном байте без знака — это (в двоичном виде) 111111112
Переведем это число в десятичную систему счисления (для простоты счета переведем сначала в 8-ную).
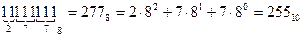
Итак, в один байт без знака можно поместить максимальное десятичное число 255.
Аналогично можно вычислить максимальное число, которое можно поместить в два байта (т.е. 16 бит).
11111111111111112=6553510.
Для чисел со знаком самый левый разряд отводится под знак. Для положительного числа этот разряд равен 0, для отрицательного — 1.
Число +12 в 8-битной разрядной сетке будет записано следующим образом: 1210=11002.

Знак ‘+’
Обратите внимание на расположение чисел в разрядной сетке: между знаковым разрядом и первым значащим разрядом числа располагаются нули.
Вычислим максимальное положительное число, которое помещается в 8 бит со знаком, т.е. под число отводится 7 бит.
знак
11111112=1778=1.82+7.81+1.80=64+56=127.
Теперь вычислим максимальное положительное число, которое помещается в 16-ти разрядную сетку со знаком.
знак
1111111111111112=7FFF16=716.163+F16.161+F16.161+F16.160=7.163+15.162+15.161+15.1=32767.
Представление отрицательных чисел существенно отличается от представления положительных чисел. Предварительно рассмотрим некоторые понятия, а именно введем определение прямого, обратного и дополнительного кодов.
5.3 Прямой, обратный и дополнительный коды.
1) Положительные числа.
Для положительных чисел прямой код равен обратному коду и равен дополнительному коду.
Прямой код Xпр двоичного числа X содержит двоичные цифровые разряды, слева записывается знак числа.
Пример.
Разместить в разрядной сетке из восьми разрядов положительное число 97.
9710=11000012.
Это же число разместим в разрядной сетке из 16 разрядов.
2) Отрицательные числа.
Отрицательные числа хранятся в памяти ЭВМ либо в обратном, либо в дополнительном кодах.
Обратный код Xобр двоичного отрицательного числа X получается следующим образом: в знаковый разряд числа записывается единица, в цифровых разрядах нули заменяются единицами, а единицы — нулями.
Запишем число -4 в обратном коде в 8-ми разрядной сетке. Двоичный код модуля исходного числа равен 1002. Обратный код получается инверсией каждого разряда двоичного кода модуля исходного числа, записанного в 8-ми разрядную сетку.
Двоичный код модуля исходного числа равен 00000100. Выполним инверсию каждого разряда .
Обратный код числа -4 записывается следующим образом:

Знаковый разряд
Дополнительный код Xдоп отрицательного числа X получается из обратного кода Xобр путем прибавления единицы к самому правому разряду (он называется младшим).
Итак, Xдоп=Xобр + 00000001, т.е.
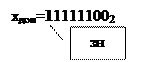 1 1
| |||||||
| (знак.разряд) | |||||||
(сложение производим в двоичной системе счисления 12+12=102)
1 1 1 1 1 1 0 0
2726252423222120
Теперь приведем полученное число в десятичную систему счисления
128+64+32+16+8+4=252
Мы получили, что дополнительный код числа –4 в десятичной системе счисления равен 252. Сложим ê-4ê+252=256. 256=28. Количество разрядов сетки было равно 8. Число 252 «дополнило» число ç–4ç до 28 = 1000000010.
Теперь сложим два двоичных числа – двоичный код числа ç-4ç в 8-разрядной сетке и дополнительный код числа –4:
 11111100
11111100
 1 000000002 мы получили 28
1 000000002 мы получили 28
Запишем общее правило получения дополнительного кода некоторого целого числа х.
 x, x>=0
x, x>=0
Xдоп =
2k - |x|, x<0, где k – количество разрядов сетки.
Есть еще одно очень простое правило получения дополнительного кода некоторого отрицательного числа.
Для получения дополнительного кода, необходимо инвертировать все разряды прямого кода модуля исходного числа начиная с самого левого разряда исключая последнюю единицу и стоящие за ней нули.
00000 100 прямой код ç-4ç
11111 100
инверсия разрядов
Определим наименьшее отрицательное число, которое можно положить в один байт со знаком. Прямой код такого числа равен -1111111. Самый левый разряд отведён под знак числа. Найдём дополнительный код числа А. Адоп = 10000000 .
Следовательно, самое маленькое отрицательное число, которое можно записать в 8-ми разрядной сетке — 27 = -128. Рассуждая таким же образом, получим, что для 16-ти разрядной сетки самое маленькое отрицательное число равно 215 или-32768.
Прямой, обратный и дополнительный коды введены для упрощения операции вычитания(или алгебраического сложения). При помощи обратного и дополнительного кодов операция вычитания сводится к операции арифметического сложения. При этом операнды представляются либо в обратном, либо в дополнительном коде. Рассмотрим конкретные примеры. Для упрощения будем рассматривать четырехразрядную сетку.
а) Вычислить х-у, где х=+6,у=-3, при этом результат является положительным числом.
Х-у=6+(-3)
хпр=хобр=хдоп=0.110; уобр=1.100; удоп=1.101
Сложение в обратных кодах:
хпр=0.110
+
уобр=1.100
10.010
+
_____1
0.011
В данном случае единица, не поместившаяся в разрядную сетку (единица переноса из знакового разряда), циклически прибавляется к правому разряду суммы кодов. Ответом является положительное двоичное число 0.0112=310.
Сложение в дополнительных кодах:
Хпр=0.100
+
удоп=1.101
10.011
¿
__________
0.011
При сложении в дополнительных кодах левая единица, вышедшая за границы разрядной сетки отбрасывается. Результатом является положительное число 310.
б) Рассмотрим второй случай: числа имеют разные знаки, но в результате получаем отрицательное число.
х=-610=-1102 и у=+310=+0112.
Хобр=1.001, хдоп=1.010, упр=уобр=удоп=0.011.
Сложение в обратных кодах:
хобр=1.001
+
упр= 0.011
1.100
В данном случае получен обратный код алгебраической суммы, необходимо перейти от обратного кода к прямому:
(х+у)обр=1.100, следовательно, (х+у)пр=-0112=-310( единица в знаковом разряде дает минус, все остальные разряды инвертируются).
Сложение в дополнительных кодах:
Хдоп=1.010
+
упр=0.011
1.101
Ответ представлен в дополнительном коде, необходимо получить прямой код алгебраической суммы.
(1.101)доп ® (1.100)обр ® -0112=-310.
в) Третий случай: оба числа отрицательные.
Х=-6=-1102, у=-3=-0112.
Хобр=1.001, хдоп=1.010,
Уобр=1.100, удоп=1.101.
Рассмотрим алгебраическое сложение в дополнительных кодах:
1.010
+
1.101
10.111
В данном случае имеет место так называемое отрицательное переполнение, так как возник перенос только из знакового разряда суммы. Следовательно, результат получился отрицательный и превышающий предельно допустимое значение для данной разрядной сетки. Сдвинем полученный результат на 1 разряд вправо, тогда(х+у)доп=(1.0111)доп. Перейдем от дополнительного кода к прямому:
(1.0111)доп ® (1.0110)обр ® (1.1001)пр = -910.
Следует отметить, что в процессе выполнения расчетов на ЭВМ может образоваться как «положительный», так и «отрицательный» ноль, причем только в дополнительном коде он имеет единственное представление. Действительно,
(+0)пр=0.00…00; (-0)пр = 1.00…00,
в обратном коде
(+0)обр=0.00…00; (-0)обр = 1.11…11,
в дополнительном коде
(+0)доп=0.00…00; (-0)доп = 0.00…00.
Следует также иметь в виду, для разрядной сетки данной длины дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных.
По этим причинам в ЭВМ для представления отрицательных чисел чаще используется дополнительный код.
И последнее очень существенное замечание:
При сложении может возникнуть ситуация, когда старший разряд суммы не помещается в отведенной под результат разрядной сетке и он «захватывает» знаковый разряд, естественно значение суммы искажается.
Пример. Пусть дана 4-х разрядная сетка со знаком, в которой должен разместиться результат от суммирования двух положительных чисел х=5 и у=7.
хпр = 0.101, упр = 0.111
0.101
+
0.111
1.100
Так как знаковый разряд равен единице, то результат воспринимается как дополнительный код и, если попробовать вывести значение суммы, допустим на экран, процессор перейдет к прямому коду:
(1.100)доп ® (1.011)обр ® -1002=-410.
Посмотрим, что получится, если под результат отвести шесть разрядов:
0.00101
+
0.00111
0.01100
(х+у)пр=(0.01100)пр=+12.
Сумма двух чисел вычислена верно.
Выполнить самостоятельно:
1. Найти дополнительные коды для чисел:-45, 123, -98, -А516, -111, -778. Формат представления данных один байт со знаком.
2. Найти дополнительные коды для чисел: -11100018, 234, -456, -АС0916, -32324, СС7816, -110012,. Формат представления данных два байта со знаком.
5.4 Представление чисел с плавающей точкой.
Математическая запись числа две целых четыре сотых выглядит так 2,04 но возможна и такая запись 0,204×10, или такая 20,4×10-1, или такая 0,0204×102... Этот ряд можно продолжать сколь угодно долго. На что вы обратили внимание? - запятая перемещается («плавает») влево или вправо, и, чтобы не изменить значение числа, мы умножаем его на 10 в отрицательной или положительной степени.
Для представления вещественных чисел в памяти ЭВМ используется формат с плавающей точкой. При этом необходимо помнить, что система вещественных чисел представимых в ЭВМ является дискретной и конечной.
В общем случае любое число N, представляемое в форме с плавающей точкой, является произведением двух сомножителей: 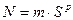 .
.
m — будем называть мантиссой числа (модуль целой части мантиссы изменяется в диапазоне от 1 до S-1 (включая эти числа), где S- основание системы счисления),
p — целочисленный порядок,
S ¾ основание системы счисления.
Различают нормализованную и экспоненциальную формы записи числа. Если мантисса является правильной дробью, у которой первая цифра после точки отлична от нуля , то число называется нормализованным.
При представлении числа в экспоненциальной форме обязательно присутствует целая часть, содержащая не более одной цифры отличной от нуля, фактически эта форма представления совпадает со стандартной математической формой записи числа.
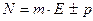
Вещественное число в ПЭВМ представлено в экспоненциальной форме.
Следовательно, при представлении чисел с плавающей точкой необходимо записать в разрядной сетке ЭВМ со своими знаками мантиссу 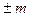 и порядок
и порядок 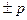 . Знак числа при этом совпадает со знаком мантиссы. Запишем число 314.6789 в экспоненциальной форме:314.6789= 3.1467890000E+2. Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в ЭВМ чисел с плавающей точкой.
. Знак числа при этом совпадает со знаком мантиссы. Запишем число 314.6789 в экспоненциальной форме:314.6789= 3.1467890000E+2. Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в ЭВМ чисел с плавающей точкой.
Кроме того, этот диапазон зависит также от основания S принятой системы счисления.
Значение произвольного числа вещественного типа представляется в ПЭВМ лишь с некоторой конечной точностью, которая зависит от внутреннего формата вещественного числа, точность представления чисел повышается с увеличением числа разрядов мантиссы.
Для того, чтобы упростить операции над порядками их сводят к действиям над целыми положительными числами путем использования так называемого смещенного порядка, который всегда положителен. смещенный порядок получается путем прибавления к порядку р некоторого целого положительного числа, значение которого зависит от конкретного формата данных.
Десятичная точка подразумевается перед левым (старшим) разрядом мантиссы, но при действиях с числом ее положение смещается влево или вправо в зависимости от двоичного порядка.
Рассмотрим представление чисел в разрядной сетке длиной 4 байта ( так называемая одинарная точность) для ПЭВМ типа РС. Изобразим разрядную сетку, состоящую из 32 разрядов и посмотрим, как эти разряды распределены.
0 1 2 3 4 5 6 7 8 … 31
    
| … |






знак мантиссы порядок мантисса
Пусть необходимо представить число –13,75 в разрядной сетке с одинарной точностью. Для этого необходимо выполнить следующие действия:
1. перевести число в двоичную систему счисления;
2. представить его в экспоненциальной форме;
3. получить исходный порядок и мантиссу;
4. получить смещенный порядок.
1) 13.7510=1101.112
75/100=3/4=3/22=0.112
2) Представим двоичное число 1101.11 в экспоненциальной форме 1101.11=1.10111E+3.
3) Исходный порядок равен 3.
Следует отметить, что целая часть двоичного числа представленного в экспоненциальной форме, всегда равна 1, поэтому в целях экономии разрядов (а следовательно увеличения диапазона представления чисел)целая часть числа не записывается в разрядную сетку.
4) Вычислим смещенный порядок (в формате с одинарной точностью к исходному порядку добавляется число 127)
Pсм=3+127=130=128+2=27+2=100000002+102=1000 00102
Рсм=100000102
Мантисса=.101112
Знак числа положительный, следовательно, самый левый разряд равен 0.
0 10000010 10111000000000000000000
знак порядок мантисса
представим полученное число в шестнадцатеричной системе счисления
0100 0001 0101 1100 0000 0000 0000 0000
Итак, мы получили шестнадцатеричное число 415С0000.
Решим обратную задачу.
Значение переменной А Представлено в формате с плавающей точкой в шестнадцатеричной системе счисления А=ВЕ200000. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.
Для решения обратной задачи необходимо выполнить следующие действия:
1) Перевести шестнадцатеричное число в двоичную систему счисления.
2) Выделить знак мантиссы(знак мантиссы совпадает со знаком числа).
3) Выделить смещенный порядок.
4) Вычислить исходный порядок.
5) Записать число, не забыв указать его целую часть, в экспоненциальной форме.
6) Перевести число из экспоненциальной формы в обычную форму записи.
7) Перевести число из двоичной системы счисления в десятичную.
Выполним перечисленные действия.
ВЕ200000=1011 1110 0010 0…0000
1 01111100 0100…0
знак порядок мантисса
Число отрицательное так как левый разряд равен 1.
Вычислим исходный порядок:
Р=Р-127=1111100-127=124-127=-3.
Запишем искомое число в экспоненциальной форме в двоичной системе счисления:
А=-1.01Е-3. Не забывайте указывать целую часть.
Представим искомое число в обычной форме записи в двоичной системе счисления:
А=-1.01Е-3=-0.001012=-0.2816=-0.15625.
Операция алгебраического сложения чисел, представленных в форме с плавающей точкой , производится несколько сложнее, чем для чисел, представленных в форме с фиксированной точкой. При выполнении ее сначала выравниваются порядки слагаемых, В результате сравнения порядков порядок меньшего по модулю числа принимается равным порядку большего, а его мантисса сдвигается вправо на число шестнадцатеричных разрядов, равное разности порядков.
В процессе сдвига мантиссы меньшего слагаемого происходит потеря младших разрядов, что вносит определенную погрешность в результат выполнения данной операции.
После выравнивания порядков производится алгебраическое сложение мантисс.
Подведём некоторые итоги по представлению числовой информации в памяти ЭВМ.
Представление числовой информации в цифровом автомате , как правило, влечёт за собой появление погрешностей, величина которых зависит от формы представления чисел и от длины разрядной сетки автомата.
Необходимо помнить о том, что для записи числа в любой форме представления отводится конечное число разрядов. Для целых чисел это обстоятельство привело к понятию наибольшего и наименьшего целого числа. Однако для каждого целого числа, не превышающего по модулю наибольшего, имеется ровно одно представление в машинном коде и, если не происходит переполнения, результат выполнения операции над целыми числами будет точным., так как дискретные множества исходных чисел однозначно отображаются на дискретное множество результатов.
Другое дело – вещественные числа. Вещественные числа образуют непрерывное множество. В памяти ЭВМ вещественные числа заменяются их кодами, которые образуют конечное дискретное множество, поэтому:
· строгие отношения между числами непрерывного множества превращаются в нестрогие для их компьютерных кодов;
· результаты вычислений содержат неизбежную погрешность, так как код вещественного числа в памяти ЭВМ является приблизительным представителем многих чисел из интервала , оценка погрешности самостоятельная и далеко не тривиальная задача;
· наряду с понятием наибольшего вещественного числа появляется понятие наименьшего числа или машинного нуля. Конкретное значение числа, которое воспринимается в вычислительной машине как машинный ноль, зависит от типа данных используемых в том или ином языке программирования.
Выполнить самостоятельно:
1) Найти представление десятичного числа А в шестнадцатеричной системе счисления в формате с плавающей точкой. Тип числа single.
А=-357.2265626; А=-0.203125; А=998.46875;
А=–657.4375; А=998.8125; А=-905,34375; А=897.5625
А=637.65625; А=56.53125; А=-4.78125.
2) Значение переменной А представлено в формате с плавающей точкой в шестнадцатеричной системе счисления. Тип переменной А-single для языка Паскаль. Найти десятичное значение переменной А.
А=C455C200; A=43D09400; A=443F9000; A=C2FF8000;
А=44071С00; A=435D2000; А=C401F000; А= С403ЕС00;
A=C3D87400; A=C3D40000; A=C411FA00; A=3F700000.
5.5 Кодирование текстовой и графической информации .
Теория кодирования информации является одним из разделов теоретической информатики. В задачи данного курса не входят вопросы теории кодирования. Коротко и упрощённо рассмотрим кодирование текстовой и графической информации.
Кодирование текстовой информации.
Кодирование текстовой информации заключается в том, что каждому текстовому символу ставится в соответствие код - целое положительное число. В зависимости от числа разрядов, отведённых под кодирование символов, все виды кодировок делятся на две группы: 8 – разрядные и 16 – разрядные. Для каждого вида кодировки символы вместе с их кодами образуют кодировочную таблицу. В кодировочной таблице первая половина кодов отводится под кодирование управляющих символов, а также цифр и букв английского алфавита. Оставшаяся часть под кодирование символов национального алфавита.
К 8 – разрядным кодировкам, включающим в себя кодировку символов русского алфавита, относятся: ASCII, ДКОИ-8, Win 1251.
16 – разрядная кодировка Unicode позволяет представить 216 различных символов. В кодовой таблице Unicode присутствуют символы всех современных национальных языков. Символы первых 128 кодов совпадают с таблицей кодов ASCII.
Кодирование изображений.
Рассмотрим растровое кодирование изображений.
Введём обозначения:
К – количество разных цветов, используемых при кодировании изображения;
n – количество битов, необходимое для кодирования цвета одной точки изображения. К и n связаны следующим образом:
К = 2n.
Пользуясь этой формулой, можно рассчитать, сколько битов необходимо для кодирования цвета одной точки, если известно количество разных цветов, с помощью которых может быть представлено изображение:
n = log2K
Количество битов, необходимое для хранения одной точки изображения, называется глубиной цвета.
Окраска одной точки экрана формируется с помощью трёх базовых цветов: красного, зелёного, синего. Эти три цвета являются основой модели RGB. С их помощью можно получить 23 разных цветов. В данном случае для кодирования каждого из трёх базовых цветов достаточно одного бита. Однако каждый базовый цвет характеризуется не только его наличием, но и интенсивностью. Яркость каждого цвета кодируется восьмиразрядным двоичным числом, т.е. глубина цвета равна 8. Следовательно, число оттенков одного базового цвета равно 28. Это означает, что из трёх базовых цветов можно получить (256)3 =
16 777 216 цветов и их оттенков. Информация о каждом пикселе в видеопамяти займёт
n = 8 × 3 = 24 бита = 3 байта.
Таким образом, для хранения одного образа экрана потребуется объём памяти, равный произведению ширины экрана на высоту экрана и на глубину цвета. Ширина и высота задаются в пикселах.
В общем случае объём памяти, необходимый для хранения растрового изображения, рассчитывается по формуле:
V = W × H×n (битов),
где W – ширина изображения в точках;
H - высота изображения в точках;
V – объём памяти, необходимый для хранения растрового изображения.
Глава 6. Логические основы ЭВМ
6.1 Основные понятия алгебры логики.
Алгебра логики (или алгебра высказываний) – это раздел математической логики, разработанный в 19 веке в трудах английского математика Джорджа Буля. В алгебре логики используют алгебраические методы для решения логических задач.
Объектами алгебры логики являются высказывания.
Высказывание – это повествовательное предложение, содержание которого можно определить как истинное или ложное. Например, высказывание «Земля – планета Солнечной системы» истинно , а о высказывании «а>b» можно сказать истинно оно или ложно , если указаны значения переменных a b. Алгебра логики отвлекается от смыслового содержания высказываний. Её интересует только один факт – истинно или ложно данное высказывание.
Истинному значению высказывания ставится в соответствие 1(TRUE), ложному 0(FALSE).
Для обращения к высказываниям им назначают имена. Например, А – это высказывание «Ласточки летают низко перед дождём», х1 – « В коробке лежит красный карандаш», х2 – «эта ручка зелёного цвета».
Высказывание абсолютно истинно, если соответствующая ей логическая величина принимает значение 1 при любых условиях Такое высказывание называется тавтологией (логическая константа 1).
Высказывание абсолютно ложно, если соответствующая ей логическая величина принимает значение 0 при любых условиях (логическая константа 0). Такое высказывание называется противоречием.
6.2 Основные логические операции.
- Инверсия – логическое отрицание. Обозначается:
 или ¬х. Читается «не х».
или ¬х. Читается «не х».
Высказывание  истинно при ложном х и ложно при истинном х.
истинно при ложном х и ложно при истинном х.
- Конъюнкция – логическое умножение. Обозначается символами:
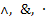 (или знак операции может быть вообще опущен), х1 их2.
(или знак операции может быть вообще опущен), х1 их2. - Дизъюнкция – логическое сложение. Обозначается: х1 ٧х2, х1 + х2, х1 или х2.
Эти три операции являются основными.
Остальные операции выражаются через первые три операции: инверсию, конъюнкцию, дизъюнкцию.
- Импликация – логическое следование. Обозначается: х1
 х2. Высказывание х1 -> x2 истинно только тогда, когда правый операнд является истинным, а левый операнд ложным.
х2. Высказывание х1 -> x2 истинно только тогда, когда правый операнд является истинным, а левый операнд ложным. - Эквивалентность(равносильность, необходимо и достаточно). Обозначается: символами
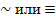 . Высказывание х1~х2 истинно тогда и только тогда, когда операнды равны.
. Высказывание х1~х2 истинно тогда и только тогда, когда операнды равны. - Сложение по модулю 2(исключающее или). Обозначается символом
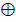 .
.
Высказывание истинно тогда и только тогда, когда операнды не равны.
Порядок выполнения операций задаётся круглыми скобками. При отсутствии скобок порядок выполнения операций следующий: инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность.
Составное высказывание (формула алгебры логики, логическое выражение) состоит из нескольких высказываний, соединённых логическими операциями. Исходные высказывания могут быть логическими переменными или логическими константами.
6.3 Основные законы и соотношения алгебры логики.
В алгебре логики имеется четыре основных закона: коммутативный (переместительный), ассоциативный (сочетательный), дистрибутивный (распределительный).
1. Переместительный закон:
· для логического сложения
х1+ х2 = х2 + х1
· для логического умножения
х1 ∙ х2 = х2 ∙ х1
2. Сочетательный закон:
· для логического закона
х1 + (х2 + х3) = (х1 + х2) + х3
· для логического умножения
х1 (х2 х3) = (х1 х2) х3
3. Распределительный закон:
· для логического сложения
х1 (х2 + х3) = х1 х2 + х1 х3
· для логического умножения
х1 + х2 х3 = (х1 + х2) (х1 + х3)
4. Закон общей инверсии (де Моргана):
· для логического сложения
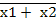 =
=  1 ∙
1 ∙  2
2
· для логического умножения
 =
=  1 +
1 +  2
2
Справедливость этих законов можно доказать табличным способом, вычисляя значения левой и правой частей доказываемого выражения для всех возможных наборов входных переменных.
Используя основные положения алгебры логики, нетрудно убедиться в справедливости следующих аксиом:
1. х + х + х + х + … + х = х (в алгебре логики нет коэффициентов)
2. х ∙ х ∙ х ∙ … ∙ х (в алгебре логики нет степеней)
3. х + 0 = х
4. х + 1 = 1
5. х ∙ 0 = 0
6. х ∙ 1 = х
7. х ∙  = 0 (закон противоречия)
= 0 (закон противоречия)
8. х +  = 1(закон исключения третьего)
= 1(закон исключения третьего)
Из распределительного закона для логического сложения и умножения вытекают следующие формулы:
· формула склеивания
х1 х2 + х1  2 = х1, т.к. х1(х2 +
2 = х1, т.к. х1(х2 + 2 ) = х1
2 ) = х1
· формулы поглощения
х1 + х1 х2 = х1, т.к. х1 (1 + х2) = х1
х1 +  1 х2 = х1 + х2
1 х2 = х1 + х2
 1 + х1 х2 =
1 + х1 х2 =  1 + х2
1 + х2
· формула свёртки
х1х2 +  1 х3+ х2х3 = х1х2 +
1 х3+ х2х3 = х1х2 +  1 х3
1 х3
6.4 Логические функции двух переменных.
Логическая функция (функция алгебры логики ФАЛ) - функция f(x1, x2, … , xn), принимающая значение , равное нулю или единице на наборе логических переменных x1, x2, … , xn.
Логическую функцию можно задать двумя способами: логической формулой или таблицей истинности. Таблица истинности задаёт значения функции на всех возможных наборах её переменных.
В алгебре логики строго доказывается, что для n переменных количество различных наборов равно2n ,а количество логических функций для n переменных равно 2 в степени 2n Рассмотрим все возможные наборы для одной переменной, для двух и трёх переменных.
Для одной переменной таких наборов два:0,1.
Для двух переменных наборов четыре:
0 0
0 1
1 0
1 1
Для трёх переменных наборов восемь:
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
В таблице 6.1. представлены различные логические функции двух переменных.
Таблица 6.1. Логические функции двух переменных
| X1 | X2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
1. Конъюнкция (логическое умножение, союз и) – функция f1(x1,x2). Принимает значение истина тогда и только тогда, когда обе переменные истинны. Во всех остальных случаях принимает значение ложь. Обозначается символами: 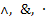 (или знак операции может быть вообще опущен). В общем случае функцию конъюнкция можно определить для n аргументов, т.е. x1, x2, … , xn.
(или знак операции может быть вообще опущен). В общем случае функцию конъюнкция можно определить для n аргументов, т.е. x1, x2, … , xn.
2. Дизъюнкция (логическое сложение, функция ИЛИ) – функция f7(x1, x2). Принимает значение ноль тогда и только тогда, когда оба аргумента равны нулю и принимает значение 1, если хотя бы один аргумент равен 1. Обозначается символом +. В общем случае функцию можно определить для n аргументов.
3. Импликация (следование) х1 в х2 функция f13 . Обращается в ноль только в том случае, когда переменная х1 равна единице, а переменная х2 равна нулю. Обозначается х1 х2.
х2.
4. Импликация х2 в х1 – функция f11(x1, x2). Обращается в ноль тогда и только тогда, когда х2 равен 1, а х1 равен 0.
5. Эквиваленция (разнозначность) – функция f9 (x1, x2). Обращается в 1 тогда и только тогда, когда обе переменные одновременно принимают одинаковые значения. Обозначается символами 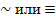 .
.
6. Исключающее или (сложение по модулю 2), функция f6 (x1, x2). Принимает значение истина в том и только в том случае, когда только один из аргументов равен 1. Обозначается символом 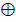 .
.
7. Штрих Шеффера – функция f14 (x1, x2). Принимает значение 0 тогда и только тогда, когда оба аргумента одновременно равны 1. Во всех остальных случаях функция равна 1. Обозначается символом /. F14 (x1, x2) = x1 / x2. Немецкий математик Д. Шеффер на основе этой функции создал алгебру, названную алгеброй Шеффера.
8. Стрелка Пирса (элемент Вебба) – функция f8 (x1, x2). Обозначается символом ↓: f8 (x1, x2) = x1 ↓ x2. Математики Ч. Пирс и Д. Вебб независимо друг от друга изучавшие свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).
9. Отрицание импликации (коимпликация) х1 в х2, функция f2 (x1, x2). Принимает значение 1 тогда и только тогда, когда х1 равен 1, а х2 равен 0. Обозначается 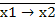 , или х1
, или х1 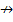 х2. Данную функцию можно рассматривать как функцию запрета со стороны переменной х2.
х2. Данную функцию можно рассматривать как функцию запрета со стороны переменной х2.
10. Отрицание импликации (коимпликация) х2 в х1, функция f4 (x1, x2). Принимает значение 1 тогда и только тогда, когда х2 равен 1, а х1 равен 0. Во всех остальных случаях значение функции 0. Функцию f4 (x1, x2) можно рассматривать как функцию запрета со стороны переменной х1.
Оставшиеся шесть логических функций f0, f3, f5, f10, f12, f15 являются либо константами, либо функциями существенным образом зависящие только от одной из переменных х1 или х2.
f0 (x1, x2) ≡ 0;
f15 (x1, x2) ≡ 1;
f3 (x1, x2) = x1;
f5 (x1, x2) = x2;
f12 (x1, x2) =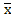 1;
1;
f10 (x1, x2) =  2.
2.
Все перечисленные логические функции являются элементарными. Приведем некоторые определения:
Определение 1. Две функции равносильны друг другу, если на всех возможных наборах переменных принимают одни и те же значения.
Определение 2. Функция [f( x1, x2, … , xn )]*, равная 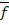 (
( 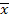 1,
1, 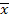 2, … ,
2, … , 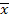 n) называется двойственной функцией к функции f(x1, x2, … , xn).
n) называется двойственной функцией к функции f(x1, x2, … , xn).
6.5 Свойства функций алгебры логики
1. Функция штрих Шеффера { / }.
Свойства функции штрих Шеффера х1 / х2 = 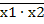 =
=  1 +
1 +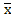 2
2
· х / х =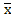 ( т.к. х / х =
( т.к. х / х =  =
=  )
)
· х / 1 = 
· х / 0 = 1
·  / 1 = х
/ 1 = х
·  / 0 = 1
/ 0 = 1
· х /  = 1
= 1
· Для функции штрих Шеффера справедливо свойство коммутативности для двух переменных, т.е. х1 / х2 = х2 / х1
Очередность операций для функции штрих Шеффера с n переменными устанавливается с помощью скобок.
Свойства ассоциативности и дистрибутивности для функции штрих Шеффера не справедливы.
2. Функция стрелка Пирса 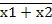 =
=  1 +
1 +  2 = х1 ↓ х2
2 = х1 ↓ х2
· х ↓ х =  (т.к. х ↓ х =
(т.к. х ↓ х =  =
=  )
)
· х ↓ 0 = 
· х ↓ 1 = 0
· х ↓  = 0
= 0
·  ↓ 1 = 0
↓ 1 = 0
·  ↓ 0 = х
↓ 0 = х
· х1 ↓ х2 = х2 ↓ х1 свойство коммутативности выполняется только для двух переменных.
Для установления приоритетов выполнения операции стрелка Пирса, обязательно должны использоваться скобки.
Для функции стрелка Пирса свойства ассоциативности и дистрибутивности несправедливы.
3. Функция сложение по модулю 2 (х1 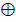 х2).
х2).
Через отрицание, конъюнкцию и дизъюнкцию функция сложения по модулю 2 выражается следующим образом:
| х1 | х2 | х1 ⊕ х2 | СДНФ |
 1 х2 1 х2
| |||
х1  2 2
| |||
х1 ⊕ х2 = х1  2 +
2 +  1 х2;
1 х2;
Функция сложения по модулю 2 обладает следующими свойствами:
· коммутативности х1 ⊕ х2 = х2 ⊕ х1
· ассоциативности х1 ⊕ (х2 ⊕ х1) = (х1 ⊕ х2) ⊕ х3
· дистрибутивности х1 (х2 ⊕ х3) = х1 х2 ⊕ х1 х3
Для этой функции справедливы аксиомы:
х ⊕ х = 0
х ⊕ 1 = 
х ⊕  = 1
= 1
х ⊕ 0 = х
х1 ⊕ х2 =  1 ⊕
1 ⊕  2
2
х1 ⊕  2 = х1~ х2
2 = х1~ х2
 1 ⊕ х2 = х1 ~ х2
1 ⊕ х2 = х1 ~ х2
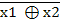 = х1 ~ х2
= х1 ~ х2
На основании аксиом и свойств можно вывести правила перевода функций отрицание, конъюнкция, дизъюнкция через функцию сложения по модулю 2 и наоборот.
 1 = х1 ⊕ 1;
1 = х1 ⊕ 1;
х1 + х2 = х1 ⊕ х2 ⊕ х1 х2
х1 х2 = (х1 ⊕ х2) ⊕ (х1 + х2)
4. Функция равнозначности (х1 ~ х2) выражается через отрицание, конъюнкцию и дизъюнкцию следующим образом:
| х1 | х2 | х1 ~ х2 | СДНФ |
 1 1  2 2
| |||
| х1 х2 |
х1 ~ х2 = х1 х2 +  1
1 2
2
Свойства функции равнозначности:
· х ~ х = 1
· х ~ 0 = 
· х ~ 1 = х
· х ~  = 0
= 0
· х1 ~ х2 =  1 ~
1 ~  2
2
· х1 ~  2 = х1 ⊕ х2
2 = х1 ⊕ х2
·  1 ~ х2 = х1
1 ~ х2 = х1 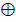 х2
х2
· 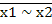 = х1 ⊕ х2
= х1 ⊕ х2
· Для двух переменных выполняется свойство коммутативности
х1 ~ х2 = х2 ~ х1
Свойства ассоциативности и дистрибутивности для этой функции не выполняются.
Функция импликация (х1 → х2) выражается через отрицание и дизъюнкцию следующим образом:
| х1 | х2 | х1 → х2 | СКНФ |
 1 + х2 1 + х2
| |||
х1 → х2 =  1 + х2
1 + х2
Для функции импликации справедливы аксиомы:
х → х = 1
х → 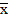 =
= 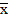
х → 1 = 1
0 → х = 1
х → 0 = 
1 →  =
= 
х1 → х2 =  2 →
2 →  1
1
х1 ∙ х2 = 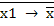 2
2
х1 + х2 =  1 → х2 =
1 → х2 =  2 → х1
2 → х1
Свойства коммутативности, ассоциативности и дистрибутивности для этой функции не справедливы.
5. Функция коимпликация (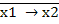 ) выражается через отрицание и конъюнкцию следующим образом:
) выражается через отрицание и конъюнкцию следующим образом:
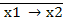 = х1
= х1  2
2
Для функции коимпликации справедливы аксиомы:
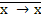 = 0
= 0
 = х
= х
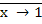 = 0
= 0
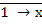 =
= 
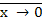 = х
= х
 = 0
= 0
х1 + х2 = 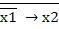
х1 х2 = 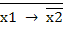
6.6 Аналитическое представление логических функций.
Рассмотренное выше представление логических функций наглядно и может быть применено для функций от любого количества переменных, однако такая запись не является компактной при анализе свойств функций алгебры логики . Проще выглядит аналитическая запись в виде формул. Но наиболее рациональным является представление логических функций в так называемых нормальных формах. Основу этих формул составляют понятия элементарных конъюнкций и дизъюнкций.
Элементарная конъюнкция (минтерм) образуется конъюнкцией конечного множества логических переменных и их инверсий, например:
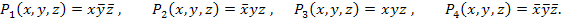
Элементарная дизъюнкция (макстерм) образуется дизъюнкцией конечного множества логических переменных и их инверсий, например:
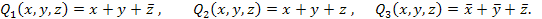
Элементарная конъюнкция принимает единичное значение только при одном из всех возможных наборов входных переменных, а элементарная дизъюнкция принимает нулевое значение только при одном из возможных наборов аргументов и единичное значение при всех других.
Следовательно, минтерм алгебраически представляет собой конъюнкцию аргументов и их инверсий, а макстерм – дизъюнкцию аргументов и их инверсий.
Количество минтермов и макстермов совпадает с количеством возможных наборов аргументов. В таблице 6.2. приведены значения элементарных конъюнкций и дизъюнкций для двух аргументов.
Таблица 6.2. Элементарные конъюнкции и дизъюнкции двух переменных
| Значения аргументов | Значения элементарных конъюнкций | Значения элементарных дизъюнкций | |||||||
| X | Y | 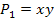
| 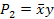
| 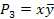
| 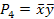
| 
| 
| 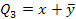
| 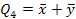
|
Количество аргументов, образующих элементарную конъюнкцию или дизъюнкцию называется ее рангом. Например, ранг минтерма 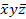 равен 3.
равен 3.
Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.
Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.
Т.е. нормальная форма – это объединение термов, включающее минтермы переменного ранга.
Количество всех термов, входящих в состав ДНФ равно количеству единичных строк таблицы истинности заданной функции.
Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции (макстермы), связанные между собой операцией конъюнкции.
1. Совершенные нормальные формы.
Одну и ту же логическую функцию можно представить различными ДНФ и КНФ. Из всей совокупности нормальных форм выделяют одну ДНФ и одну КНФ, а именно такие формы, которые являются инверсными по отношению друг к другу, т.е. если одна из них равна «1», то другая при этом равна «0», и наоборот. Эти формы называются совершенными нормальными формами.
Дизъюнктивная совершенная нормальная форма (СДНФ) отвечает следующим требованиям:
- в ней нет двух одинаковых элементарных конъюнкций;
- ни одна конъюнкция в ней не содержит одинаковых переменных;
- ни одна конъюнкция не содержит двоичную переменную с ее инверсией;
- все конъюнкции являются элементарными;
- все конъюнкции имеют одинаковый ранг.
Для представления функции в СДНФ может быть использована также операция Å.
Сформулируем требования, которые предъявляются к операции связывающей элементарные минтермы:
1) Если какой-либо терм 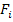 = 1, то функция должна быть равна 1.
= 1, то функция должна быть равна 1.
2) Если какой-либо терм 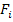 = 0, то функция может быть равна 1.
= 0, то функция может быть равна 1.
3) Необходимо, чтобы при значениях термов 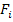 = 0 функция была равна нулю.
= 0 функция была равна нулю.
Табличное представление операций отвечающих требованиям имеет вид, представленный в таблицах 6.3. и 6.4.3:
Таблица 6.3. Таблица6.4.

| 
| D=+ |

| 
| D=Å |
Любая таблично заданная ФАЛ может быть представлена в следующей аналитической форме:
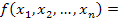
 , где
, где
 - элементарный минтерм; знак D обозначает операции +, Å;
- элементарный минтерм; знак D обозначает операции +, Å;
k – количество наборов, на которых функция равна 1.
Конъюнктивная совершенная нормальная форма (КСНФ) отвечает следующим требованиям:
- в ней нет двух одинаковых элементарных дизъюнкций;
- ни одна дизъюнкция в ней не содержит двух одинаковых переменных;
- ни одна дизъюнкция не содержит переменную вместе с ее инверсией;
- все дизъюнкции имеют один и тот же ранг.
Чтобы определить, какие операции могут связывать элементарные дизъюнкции, изложим следующие требования:
1) Если какой-либо терм 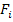 = 0, то функция должна быть равна 0.
= 0, то функция должна быть равна 0.
2) Если все термы 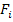 = 0, то функция равна 1.
= 0, то функция равна 1.
Выполняя эти требования можно привести к операциям конъюнкции и равнозначности (таблица 6.5. и 6.6):
Таблица 6.5. Таблица 6.6.

| 
| & |

| 
| º |
Вывод: любая таблично заданная ФАЛ может быть задана в аналитической форме:
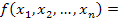
 , где
, где
знак D обозначает операции & и º, k – количество двоичных наборов, для которых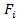 =0.
=0.
В алгебре логики строго доказывается, что любая логическая функция, кроме 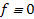 , представима в ДСНФ, любая функция, кроме
, представима в ДСНФ, любая функция, кроме 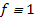 , представима в КСНФ.
, представима в КСНФ.
Формулы в ДСНФ или КСНФ можно получить по табличному представлению логической функции.
Для образования ДСНФ необходимо выполнить следующие действия:
1) по каждому набору двоичных переменных, при котором логическая функция принимает значение 1, составить элементарные конъюнкции;
2) в элементарные конъюнкции записать без инверсии переменные, заданные единицей в соответствующем наборе, и с инверсией – переменные заданные нулем;
3) соединить элементарные конъюнкции знаком операции дизъюнкции или операции сложение по модулю 2.
Для образования КСНФ необходимо выполнить аналогичную последовательность действий:
1) по каждому набору двоичных переменных, при котором логическая функция принимает значение 0, составить элементарные дизъюнкции;
2) в элементарные дизъюнкции записать без изменения переменные, заданные нулем в соответствующем наборе, и с инверсией – переменные заданные единицей;
3) соединить элементарные дизъюнкции знаком конъюнкции.
Пример.
Пусть задана некоторая функция 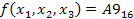 (см таблицу 6)
(см таблицу 6)
Получим для заданной функции СДНФ и СКНФ.
Функция  принимает значение 1 для четырех наборов и значение 0 для других четырех наборов.
принимает значение 1 для четырех наборов и значение 0 для других четырех наборов.
| Значения аргументов | Значения функции | ДСНФ | КСНФ | ||
| X | Y | z | 
| ||
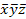
| - | ||||
| - | 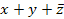
| ||||
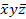
| - | ||||
| - | 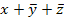
| ||||
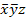
| - | ||||
| - | 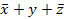
| ||||
| - | 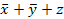
| ||||
| xyz | - |
Функция в СДНФ состоит из логической суммы четырех элементарных конъюнкций третьего ранга:

Функция в СКНФ является логическим произведением четырех элементарных дизъюнкций третьего ранга:
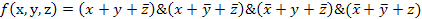
Совершенная нормальная форма отличается от нормальной формы тем, что всегда содержит термы только максимального ранга и дает однозначное представление функции.
Произвольная нормальная дизъюнктивная форма переводится в СДНФ следующим образом:
пусть 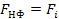 , тогда
, тогда
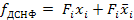 , где
, где 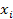 - переменная, которая не входит в данный терм
- переменная, которая не входит в данный терм  .
.
Пример.
Логическую функцию, заданную в ДНФ преобразовать в СДНФ.
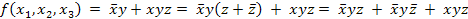 .
.
Произвольная КНФ переводится в СКНФ логическим умножением дизъюнкции младшего ранга на конъюнкцию 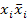 , где
, где 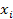 – переменная, которая не входит в данный терм.
– переменная, которая не входит в данный терм.
Пусть  , тогда
, тогда

Пример.

При использовании аналитических форм представления обычно стремятся к упрощению логических функций.
6.7 Системы функций алгебры логики.
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики.
Теорема Жегалкина. Любая булева функция может быть представлена многочленом вида 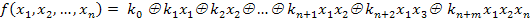 , где
, где  – коэффициент, принимающий значения 0 или 1.
– коэффициент, принимающий значения 0 или 1.
Теорема Жегалкина дает возможность представить любую логическую функцию в виде полиномов разной степени, существует несколько классов ФАЛ, которые также важны для логического анализа.
Класс линейных функций (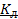 ). Булева функция называется линейной, если она представляется полиномом первой степени:
). Булева функция называется линейной, если она представляется полиномом первой степени:
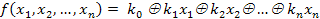 .
.
Количество линейных функций равно 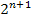 .
.
Например, при n=2 количество линейных функций равно 8.
1) 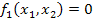 ;
;
2) 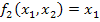 ;
;
3) 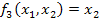 ;
;
4) 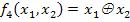 ;
;
5)  ;
;
6) 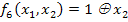 ;
;
7) 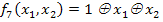 ;
;
8) 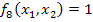 .
.
Класс функций, сохраняющих 0 (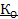 ).
).
Если функция на нулевом наборе переменных равна нулю, то говорят, что функция сохраняет ноль:
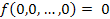 .
.
Класс функций, сохраняющих 1 (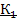 ).
).
Если функция на единичном наборе переменных равна 1, то говорят, что функция сохраняет единицу:
 .
.
Класс монотонных функций ( ).
).
Функция алгебры логики называется монотонной, если при любом возрастании набора значения этой функции не убывают.
Класс самодвойственных функций ( ).
).
Функция алгебры логики является самодвойственной, если на каждой паре противоположных наборов она принимает противоположные значения, т.е.:
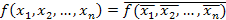 .
.
Все названные функции обладают существенным свойством: любая функция алгебры логики, полученная с помощью операции суперпозиции и подстановки из функций одного класса, обязательно будет принадлежать этому же классу. При этом система логических функций называется функционально полной, если любую логическую функцию можно представить в аналитической форме через функции, взятые в любом конечном числе экземпляров каждая.
Базисом называется полная система ФАЛ, с помощью которой любая ФАЛ может быть представлена суперпозицией исходных функций.
Теорема Поста-Яблонского. Для того, чтобы система ФАЛ была полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию:
не сохраняющую ноль,
не сохраняющую единицу,
не являющуюся линейной,
не являющуюся монотонной,
не являющуюся самодвойственной.
Проблема простейшего представления логических функций сводится не только к выбору не только базиса, но и формы наиболее экономного представления этих функций.
Перечень базисов.
2. - базис Шеффера; 3. - коипликация, эквиваленция; 4. - импликативный базис;Пример.
Пусть задана логическая функция с помощью таблицы истинности:F(a,b,c) = A916.
Представить её в базисе Жегалкина, используя не более 4 - х элементов.
Решение.
| A | B | c | F | |
| * | ||||
| * | ||||
| * | ||||
| * |
Построим СДНФ для заданной функции.
Так как задан базис Жегалкина, целесообразно элементарные минтермы соединить операцией сложение по модулю 2.
СДНФ: ¬a ¬b ¬c ⊕ ¬ab ¬c ⊕ a ¬b ¬c ⊕ abc.
Упростим полученную формулу:
¬a ¬b ¬c ⊕ ¬ab ¬c ⊕ a ¬b ¬c ⊕ abc = ¬a ¬c(¬b ⊕ b) ⊕ a (¬b ¬c ⊕ bc) = ¬a ¬c ⊕ a(b~c) = ¬a ¬c ⊕ a(b ⊕ ¬c) = ¬a ¬c ⊕ ab ⊕ a ¬c = ¬c(¬a⊕ a) ⊕ ab = ¬c ⊕ ab =
c ⊕ ab⊕1.
Рассмотрим практическое применение изложенного материала.
Задача 1. На вопрос, кто из трех студентов изучал логику, был получен следующий ответ: если изучал первый, то изучал и второй, но неверно, что если… Решение. Обозначим через В1, В2, В3 высказывания, состоящие в том, что соответственно первый, второй, третий студенты изучали…Решение логических задач с помощью таблиц истинности.
Задача.
А, В и С подозреваются в ограблении банка. Есть три версии:
- либо С ограбил банк, либо B или А ограбили банк;
- если С участвовал в ограблении, то А и B тоже участвовали;
- участие А в ограблении равносильно тому, что В участвовал, а С не участвовал.
Все версия оказались ложными. Кто ограбил банк?
РЕШЕНИЕ:
Обозначим
A=1  А ограбил банк.
А ограбил банк.
В=1  В ограбил банк.
В ограбил банк.
С=1  С ограбил банк.
С ограбил банк.
Составим формулы (версии):
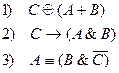
Построим таблицы истинности для каждой из формул и найдем строку, в которой все логические формулы принимают значение 0.
| A | B | С | С ⊕ (А+В) | С→(А&В) | А≡(В&¬C) |
Такая строка в таблице единственная – при значениях А = 1, В = 0, С = 1.
ОТВЕТ: А и С ограбили банк.
Задачи для самостоятельного решения.
1. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом стоит… 2. В соревнованиях по гимнастике участвуют Алла, Валя, Сима и Даша.… 1) Сима будет первой, Валя – второй;Регистры.
Регистр процессора — встроенная сверхбыстрая оперативная память (СОЗУ) процессора, предназначенная для хранения промежуточных результатов вычисления… Большая часть регистров процессора используется для внутренных целей и… Пользовательские регистры. Эти регистры позволяют программисту сократить число обращений к основной памяти,…Счётчики.
Дешифраторы. Комбинационная логическая схема, преобразующая поступающий на входы код в…Глава 7. Контроль работы цифрового автомата
7.1 Кодирование информации как средство обеспечения контроля работы автомата
Коды как средство тайнописи появились в глубокой древности. Кодирование (шифрование ) появилось около четырех тысяч лет тому назад. Первым известным примером шифра считается египетский текст, созданный примерно в 1900 г. до н. э., в котором вместо обычных для египтян иероглифов ,использовались не совпадающие с ними символы.
Одним из самых известных методов кодирования (шифрования) является метод Цезаря, который римский император если и не изобрел, то, по крайней мере, активно им пользовался. Не имея доверия к своим посыльным, он шифровал письма элементарной заменой А на D, В на Е и так далее по латинскому алфавиту. К примеру, при таком кодировании последовательность ABC была бы записана как DEF. Известно, что еще древнегреческий историк Геродот в V в. до н. э., приводил примеры писем, понятных лишь адресату. Над созданием различных секретных шифров работали такие известные ученые средневековья, как Ф. Бэкон, Д. Кардано и др. Появлялись очень хитрые шифры и коды, которые, однако, с течением времени расшифровывались и переставали быть секретом. Первым кодом, предназначенным для передачи сообщений по каналам связи, был код С. Морзе, содержащий разное количество символов для кодирования букв и цифр. Затем появился код Ж. Бодо, используемый в телеграфии, в котором все буквы или цифры содержат одинаковое количество символов. В качестве символов может выступать наличие или отсутствие (пробел) импульса в электрической цепи в данный момент. Коды, использующие два различных элементарных сигнала, называются двоичными. Эти сигналы удобно обозначать символами 0 и 1. Тогда кодовое слово будет состоять из последовательностей нулей и единиц. Двоичное кодирование тесно связано с принципом дихотомии, который реализуется в графическом методе представления двоичной информации в виде графов. В предыдущих главах были рассмотрены общие и конкретные вопросы кодирования информации в цифровом автомате. Однако эти методы сами по себе еще не обеспечивают правильность выполнения того или иного алгоритма. Рассмотренные ранее алгоритмы выполнения арифметических операций обеспечат правильный результат только в случае, если машина работает без нарушений. При возникновении какого-либо нарушения нормального функционирования результат будет неверным, однако пользователь об этом не узнает, если не будут предусмотрены меры, сигнализирующие о появлении ошибки. Следовательно, с одной стороны, разработчиками машины должны быть предусмотрены меры для создания системы обнаружения возможной ошибки, а с другой стороны, должны быть проработаны меры, позволяющие исправить ошибки. Эти функции следует возложить на систему контроля работы цифрового автомата.
Введём следующее определение.
Система контроля — совокупность методов и средств, обеспечивающих определение правильности работы автомата в целом или его отдельных узлов, а также автоматическое исправление ошибки.
Ошибки в работе цифрового автомата могут быть вызваны либо выходом из строя какой-либо детали, либо отклонением от нормы параметров, например изменением напряжения питания или воздействием внешних помех. Вызванные этими нарушениями ошибки могут принять постоянный или случайный характер. Постоянные ошибки легче обнаружить и выявить. Случайные ошибки, обусловленные кратковременными изменениями параметров, наиболее опасны, и их труднее обнаружить.
Поэтому система контроля должна строиться с таким расчетом, чтобы она позволяла обнаружить и по возможности исправить любые нарушения.
При этом надо различать следующие виды ошибок результата:
1) возникающие из-за погрешностей в исходных данных;
2) обусловленные методическими погрешностями;
3) появляющиеся из-за возникновения неисправностей в работе машины.
Первые два вида ошибок не являются объектом для работы системы контроля. Погрешности перевода или представления числовой информации в разрядной сетке автомата приведут к возникновению погрешности в результате решения задачи. Эту погрешность можно заранее рассчитать и, зная ее максимальную величину, правильно выбрать длину разрядной сетки машины. Методические погрешности также учитываются предварительно.
Проверка правильности функционирования отдельных устройств машины и выявление неисправностей может осуществляться по двум направлениям:
· профилактический контроль, задача которого — предупреждение появления возможных ошибок в работе;
· оперативный контроль, задача которого — проверка правильности выполнения машиной всех операций.
Решение всех задач контроля становится возможным только при наличии определенной избыточности информации. Избыточность может быть создана либо аппаратными (схемными) средствами, либо логическими или информационными средствами.
К методам логического контроля, например, можно отнести следующие приемы. В ЭВМ первого и второго поколения отсутствие системы оперативного контроля приводило к необходимости осуществления «двойного счета», когда каждая задача решалась дважды и в случае совпадения ответов, принималось решение о правильности функционирования ЭВМ.
Если в процессе решения какой-то задачи вычисляются тригонометрические функции, то для контроля можно использовать известные соотношения между этими функциями, например sin2 α+ cos2 α = 1 . Если это соотношение выполняется с заданной точностью на каждом шаге вычислений, то можно с уверенностью считать, что ЭВМ работает правильно.
Вычисление определенного интеграла с заданным шагом интегрирования можно контролировать сравнением полученных при этом результатов с теми результатами, которые соответствуют более крупному шагу. Такой «сокращенный» алгоритм даст, видимо, более грубые оценки и по существу требует дополнительных затрат машинного времени.
Все рассмотренные примеры свидетельствуют о том, что такие методы контроля позволяют лишь зафиксировать факт появления ошибки, но не определяют место, где произошла эта ошибка. Для оперативного контроля работы ЭВМ определение места, где произошла ошибка, т. е. решение задачи поиска неисправности, является весьма существенным вопросом.
Задача кодирования информации представляется как некоторое преобразование числовых данных в заданной системе счисления. В частном случае эта операция может быть сведена к группированию символов (представление в виде триад или тетрад) или представлению в виде символов (цифр) позиционной системы счисления. Так как любая позиционная система не несет в себе избыточности информации и все кодовые комбинации являются разрешенными, использовать такие системы для контроля не представляется возможным.
Систематический код — код, содержащий в себе кроме информационных контрольные разряды.
В контрольные разряды записывается некоторая информация об исходном числе. Поэтому можно говорить, что систематический код обладает избыточностью. При этом абсолютная избыточность будет выражаться количеством контрольных разрядов k, а относительная избыточность — отношением k/n , где n = m + k — общее количество разрядов в кодовом слове (m — количество информационных разрядов).
Понятие корректирующей способности кода обычно связывают с возможностью обнаружения и исправления ошибки. Количественно корректирующая способность кода определяется вероятностью обнаружения или исправления ошибки.
Корректирующая способность кода связана также с понятием кодового расстояния.
Кодовое расстояние d(A, В) для кодовых комбинаций А и В определяется как вес третьей кодовой комбинации, которая получается поразрядным сложением исходных комбинаций по модулю 2.
Вес кодовой комбинации V(A) — количество единиц, содержащихся в кодовой комбинации.
Пример 7.1. Найти вес и кодовое расстояние для комбинаций A = 011011100,
B = 100111001
Решение. Вес для кодовых комбинаций V(A) = 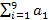 = 5; V(B) =
= 5; V(B) = 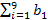 = 5 .
= 5 .
Находим кодовую комбинацию С= A ⊕ B = 111100101, для которой определяется вес,
равный кодовому расстоянию для A и В: V(C) = d(A,B) =  = 6
= 6
Ответ d(A.B) = 6.
Коды можно рассматривать и как некоторые геометрические (пространственные) фигуры. Например, триаду можно представить в виде единичного куба, имеющего координаты вершин, которые отвечают двоичным символам (рис. 8.1). В этом случае кодовое расстояние воспринимается как сумма длин ребер между соответствующими вершинами куба (принято, что длина одного ребра равна 1). Оказывается, что любая позиционная система отличается тем свойством, что минимальное кодовое расстояние равно 1 (рис. 8.2, а).
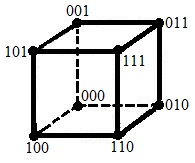
Рис. 7.1. Геометрическое представление кодов
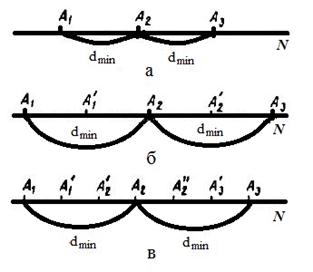
Рис. 7.2. Кодовые расстояния
В теории кодирования показано, что систематический код способен обнаружить ошибки только тогда, когда минимальное кодовое расстояние для него больше или равно 2t, т.е.

где t — кратность обнаруживаемых ошибок (в случае одиночных ошибок t = 1 и т. д.).
Это означает, что между соседними разрешенными кодовыми словами должно существовать по крайней мере одно кодовое слово (рис. 8.2, б, в).
В тех случаях, когда необходимо не только обнаружить ошибку, но и исправить ее (т.е. указать место ошибки), минимальное кодовое расстояние должно быть
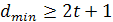
Существуют коды, в которых невозможно выделить абсолютную избыточность. Пример таких кодов — Д-коды, где количество разрешенных комбинаций меньше количества возможных комбинаций. Неявная избыточность характерна также для кодов типа «k из n». Примером является код «2 из 5», который часто используется для представления информации. Суть его в том, что в слове из пяти разрядов только два разряда имеют единичное значение.
7.2 Методы эффективного кодирования информации
Информационную избыточность можно ввести разными путями. Рассмотрим один из путей эффективного кодирования.
В ряде случаев буквы сообщений преобразуются в последовательности двоичных символов. Учитывая статистические свойства источника сообщения, можно минимизировать среднее число двоичных символов, требующихся для выражения одной буквы сообщения, что при отсутствии шума позволит уменьшить время передачи.
Такое эффективное кодирование базируется на основной теореме Шеннона для каналов без шума, в которой доказано, что сообщения, составленные из букв некоторого алфавита, можно закодировать так, что среднее число двоичных символов на букву будет сколь угодно близко к энтропии источника этих сообщений, но не меньше этой величины.
Теорема не указывает конкретного способа кодирования, но из нее следует, что при выборе каждого символа кодовой комбинации необходимо стараться, чтобы он нес максимальную информацию. Следовательно, каждый символ должен принимать значения 0 и 1 по возможности с равными вероятностями и каждый выбор должен быть независим от значений предыдущих символов.
При отсутствии статистической взаимосвязи между буквами конструктивные методы построения эффективных кодов были даны впервые К. Шенноном и И. Фано. Их методики существенно не различаются, поэтому соответствующий код получил название кода Шеннона-Фано.
Следует отметить, что вторая теорема Шеннона относится к реальным каналам связи и гласит следующее:
При передаче информации по каналу с шумом всегда имеется способ кодирования, при котором сообщение будет передаваться со сколь угодно высокой достоверностью, если скорость передачи не превышает пропускной способности канала.
7.3 Кодирование по методу четности-нечетности
Если в математическом коде выделен один контрольный разряд (k = 1), то к каждому двоичному числу добавляется один избыточный разряд и в него записывается 1 или 0 с таким условием, чтобы сумма цифр в каждом числе была по модулю 2 равна 0 для случая четности или 1 для случая нечетности. Появление ошибки в кодировании обнаружится по нарушению четности (нечетности). При таком кодировании допускается, что может возникнуть только одна ошибка. В самом деле, для случая четности правильной будет только половина возможных комбинаций. Чтобы одна допустимая комбинация превратилась в другую, должно возникнуть по крайней мере два нарушения или четное число нарушений. Пример реализации метода четности представлен в таблице 7.1.
Таблица 7.1
| Число | Контрол.ьный разряд | Проверка |
| 1 - нарушение |
Такое кодирование имеет минимальное кодовое расстояние, равное 2.
Можно представить и несколько видоизмененный способ контроля по методу четности — нечетности. Длинное число разбивается на группы, каждая из которых содержит l разрядов. Контрольные разряды выделяются всем группам по строкам и по столбцам согласно следующей схеме:
| A1 | A2 | A3 | A4 | A5 | K1 |
| A6 | A7 | A8 | A9 | A10 | K2 |
| A11 | A12 | A13 | A14 | A15 | K3 |
| A16 | A17 | A18 | A19 | A20 | K4 |
| A21 | A22 | A23 | A24 | A25 | K5 |
| K6 | K7 | K8 | K9 | K10 |
Увеличение избыточности информации приводит к тому, что появляется возможность не только обнаружить ошибку, но и исправить ее. Пусть произошла неисправность в каком-то из разрядов этого числа (представим, что разряд a18 изменил состояние, т. е. a18 = 1). Это приведет к тому, что при проверке на четность сумма 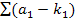 по соответствующим строкам и столбцам изменится для значений, которые содержат элемент a18, т. е. это будет четвертая сверху строка и третий слева столбец. Следовательно, нарушение четности по этой строке и столбцу можно зафиксировать, что в конечном счете означает обнаружение не только самой ошибки, но и места, где возникла ошибка. Изменив содержимое отмеченного разряда (в данном случае a18) на противоположное, можно исправить ошибку.
по соответствующим строкам и столбцам изменится для значений, которые содержат элемент a18, т. е. это будет четвертая сверху строка и третий слева столбец. Следовательно, нарушение четности по этой строке и столбцу можно зафиксировать, что в конечном счете означает обнаружение не только самой ошибки, но и места, где возникла ошибка. Изменив содержимое отмеченного разряда (в данном случае a18) на противоположное, можно исправить ошибку.
Контроль по методу чётности – нечётности широко используют в ЭВМ для контроля записи, считывания информации в запоминающих устройствах на магнитных носителях, а также при выполнении арифметических операций.
7.3 Коды Хэминга
Коды, предложенные американским ученым Р. Хэмингом, способны не только обнаружить, но и исправить одиночные ошибки. Эти коды — систематические.
Основная идея состоит в добавлении к информационным битам несколько битов чётности, каждый из которых контролирует определённые информационные биты. Если пронумеровать все передаваемые биты, начиная с первого слева направо ( напомним, что информационные биты нумеруются с нуля и справа налево), то контрольными оказываются биты, номера которых равны степеням числа 2, а все остальные являются информационными. Например, для 8 – разрядного информационного кода контрольными окажутся разряды с номерами 1,2,4,8.
Номера контролируемых битов для каждого проверочного приведены в табл. 7.2.
Таблица 7.2.
| Проверочные биты | Контролируемые биты |
| 1,3,5,7,9,11,13,15, 17, 19, 21,… | |
| 2,3,6,7,10,11,14,15,18,19,22,… | |
| 4,5,6,7,12,13,14,15,20,21,22, 23,… | |
| 8,9,10,11,12,13,14,15,24,25, 26,… | |
| 16, 17, 18, 19,20, 21, 22, 23, 24, 25, 26,… | |
| 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, … |
Легко усматривается принцип выделения контролируемых разрядов: для любого номера проверочного разряда (n), начиная с него, n разрядов подряд оказываются проверяемыми, затем группа n непроверяемых разрядов,далее происходит чередование групп.
Пример 7.2.Пусть вместо последовательности 0 0 0 1 1 1 0 1 1 1 0 1 пришла следующая:
0 0 0 1 0 1 0 1 1 1 0 1
1 2 3 4 5 6 7 8 9 10 11 12
Анализируем состояния контрольных битов в соответствии с табл. 7.2.
Бит 1 – неверно, т.е. ошибка находится в каком – либо бите с нечётным номером.
Бит 2 – верно, следовательно, биты с нечётными номерами 3, 7, 11 – верны (т.е. – ошибка в 5 или 9).
Бит 4 – неверно, значит ошибка может содержаться только в 5- м бите.
Таким образом, однозначно устанавливается, что ошибочным является 5 –й разряд, остаётся исправить его значение на противоположное и, тем самым, восстановить правильную последовательность.
На основании сказанного можно сформулировать простой алгоритм проверки и исправления передаваемой последовательности бит в представлении Хемминга:
1. произвести проверку всех битов чётности;
2. если все биты чётности верны, то перейти к п.5;
3. вычислить сумму номеров всех неправильных битов чётности;
4. инвертировать содержимое бита, номер которого равен сумме, найденной в п.3;
5. исключить биты чётности, передать правильный информационный код.
Избыточность кодов Хемминга для различных длин передаваемых последовательностей приведена в табл. 7.3.
Таблица 7.3.
| Число информационных битов | Число контрольных битов | Избыточность |
| 1.50 | ||
| 1.31 | ||
| 1.06 |
Из сопоставления видно, что выгоднее передавать и хранить более длинные последовательности битов. Безусловно, данный способ кодирования требует увеличения объёма памяти компьютера приблизительно на одну треть при 16 – битной длине машинного слова, однако, использование кодов Хемминга позволяет автоматически исправлять одиночные ошибки.
Глава 8. Прикладное программное обеспечение
К прикладному программному обеспечению (application software) относятся компьютерные программы, написанные для пользователей или самими пользователями, для задания компьютеру конкретной работы.
Из-за огромного разнообразия прикладного программного обеспечения (ППО) существует множество вариантов его классификации. Наиболее общая классификация предполагает разделение ППО на два основных класса:
1. Прикладные программы общего назначения. К таким относятся программы, обеспечивающие выполнение наиболее часто используемых, универсальных задач (текстовые редакторы, табличные процессоры, графические редакторы, Интернет-клиенты и т.п.).
2. Прикладные программы специального (профессионального) назначения. Программы этого класса ориентированы на достаточно узкую предметную область, (издательские системы; САПР - системы автоматизированного проектирования; банковские, бухгалтерские программы; программы 3D-графики; программы видеомонтажа; нотные редакторы и т.д.).
9.1 Текстовые редакторы
Все многообразие современных текстовых редакторов условно можно разбить на три основные группы:
1. К первой относятся простейшие текстовые редакторы, обладающие минимумом возможностей и способные работать с документами в обычном текстовом формате .txt, который, как известно, при всей своей простоте и всеобщей поддержке совершенно не позволяет более или менее прилично форматировать текст. К этой группе редакторов можно отнести как входящие в комплект поставки ОС семейства Windows редакторы WordPad и совсем малофункциональный NotePad (Блокнот), и множество аналогичных продуктов других производителей (Atlantis, EditPad, Aditor Pro, Gedit и т.д.).
2. Промежуточный класс текстовых редакторов включает в себя достаточно широкие возможности по части оформления документов. Они работают со всеми стандартными текстовыми файлами(TXT, RTF, DOC). К таким программам можно отнести Microsoft Works, Лексикон.
3. К третьей группе относятся мощные текстовые процессоры, такие, как Microsoft Word или StarOffice Writer. Они выполняют практически все операции с текстом. Большинство пользователей использует именно эти редакторы в повседневной работе.
Основными функциями текстовых редакторов и процессоров являются:
- ввод и редактирование символов текста;
- возможность использования различных шрифтов символов;
- копирование и перенос части текста с одного места на другое или из одного документа в другой;
- контекстный поиск и замена частей текста;
- задание произвольных параметров абзацев и шрифтов;
- автоматический перенос слов на новую строку;
- автоматическую нумерацию страниц;
- обработка и нумерация сносок;
- создание таблиц и построение диаграмм;
- проверка правописания слов и подбор синонимов;
- построение оглавлений и предметных указателей;
- распечатка подготовленного текста на принтере и т.п.
Также практически все текстовые процессоры обладают следующими функциями:
- поддержка различных форматов документов;
- многооконность, т.е. возможность работы с несколькими документами одновременно;
- вставка и редактирование формул;
- автоматическое сохранение редактируемого документа;
- работа с многоколоночным текстом;
- возможность работы с различными стилями форматирования;
- создание шаблонов документов;
- анализ статистической информации.
Сегодня практически все мощные текстовые редакторы входят в состав интегрированных программных пакетов, предназначенных для нужд современного офиса. Так, например, Microsoft Word входит в состав самого популярного офисного пакета Microsoft Office.
9.2 Электронные таблицы
Электронные таблицы предоставляют комплексные средства для хранения различных типов данных и их обработки. В некоторой степени они аналогичны системам управления базами данных, но основной акцент смещен не на хранение массивов данных и обеспечение к ним доступа, а на преобразование данных, причем в соответствии с их внутренним содержанием. В отличие от баз данных, которые обычно содержат широкий спектр типов данных (от числовых и текстовых до мультимедийных), для электронных таблиц характерна повышенная сосредоточенность на числовых данных. Зато электронные таблицы предоставляют более широкий спектр методов для работы с данными числового типа.
Основное свойство электронных таблиц состоит в том, что при изменении содержания любых ячеек таблицы может происходить автоматическое изменение содержания во всех прочих ячейках, связанных с измененными соотношением, заданным математическими или логическими выражениями (формулами). Простота и удобство работы с электронными таблицами снискали им широкое применение в сфере бухгалтерского учета, в качестве универсальных инструментов анализа финансовых, сырьевых и товарных рынков, доступных средств обработки результатов технических испытаний, то есть всюду, где необходимо
9.3 Система управления базами данных (СУБД)
Основные функции СУБД
Классификации СУБД
По модели данных
Примеры:
- Иерархические
- Сетевые
- Реляционные
- Объектно-ориентированные
По степени распределённости
- Локальные СУБД (все части локальной СУБД размещаются на одном компьютере)
- Распределённые СУБД (части СУБД могут размещаться на двух и более компьютерах).
По способу доступа к БД
На данный момент файл-серверная технология считается устаревшей. Клиент-серверные Клиент-серверная СУБД располагается на сервере вместе с БД и осуществляет… Встраиваемая СУБД — СУБД, которая может поставляться как составная часть некоторого программного продукта, не требуя…Глава 9. Методические рекомендации по решению задач в курсе информатики
В данной главе рассмотрим решение типовых задач курса информатики.
9.1 Измерение информации. Вероятностный подход.
Количество информации, содержащееся в сообщении о том, что произошло одно из N равновероятных событий равно
I = log2N. (формула Хартли)
Задача 1. В корзине лежат 8 клубов ниток различных цветов. Сколько бит информации несёт сообщение о том, что из корзины вынули клубок красного цвета?
Решение. Результат вытаскивания из коробки любого из 8 клубков – событие равновероятное, поэтому используем формулу Хартли: I = log2N, где N = 8, следовательно I = 3.
Ответ: 3 бита.
Задача 2. Кодовый замок сейфа должен допускать не менее 15 000 уникальных комбинаций. Код устанавливается с помощью трехпозиционных переключателей. Сколько таких переключателей необходимо использовать в конструкции замка?
Более общая формула выглядит следующим образом:x = logaN,
Где N – количество уникальных комбинаций;
х – требуемое количество переключателей;
а – число состояний, в которых может находится каждый переключатель.
Решение. х = log315000. Результат округляется до ближайшего целого.
Ответ: х = 9.
9.2 Арифметические основы ЭВМ.
Задача 1. Вычислить сумму двух чисел А+В, где
А =420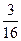 представлено в десятичной системе счисления,
представлено в десятичной системе счисления,
В=77.37 представлено в восьмеричной системе счисления.
Ответ представить в четверичной системе счисления.
РЕШЕНИЕ:
Переведем число А в 16-ую, а затем в 2-ую систему счисления:
420=1∙162+10∙161+4∙160=1А416
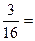 3∙16-1=0,316
3∙16-1=0,316
Итак, A=1A4,316=1 1010 0100,00112.
Переведем число B в 2-ую систему счисления:
B=77,378=111 111,011 1112
Вычислим сумму А+В=1 11 10 00 11,10 10 112=13203,2234.
ОТВЕТ: 13203,223
Образцы заданий к теме «Арифметические основы ЭВМ».
2. Представить в виде обыкновенной дроби в десятичной системе счисления…Представление целых чисел. Формат с фиксированной точкой.
Образец задания:Представление действительных чисел в памяти ЭВМ. Формат с плавающей точкой.
2.Найти десятичное значение числа A= 42E3C000 , представленного в шестнадцатеричной системе счисления в формате с плавающей точкой. Тип числа - single для basic или pascal и float - для c.Таблица КС
| Наименование элемента | Условное обозначение | Название и логическая запись функции | ||||||||
| И | 
| Конъюнкция: y=x1&x2 y=x1x2 | ||||||||
| ИЛИ | 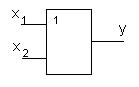
| Дизъюнкция: y=x1Vx2 y=x1+x2 | ||||||||
| НЕ | 
| Инверсия: y=x y = ¬x | ||||||||
| ИЛИ-НЕ | 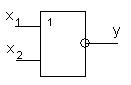
| Стрелка Пирса: ______ y=x1Vx2 y=x1↑x2 | ||||||||
| И-НЕ | 
| Штрих Шеффера: ____ y=x1x2 y=x1/x2 | ||||||||
| Элемент реализует функцию импликация | 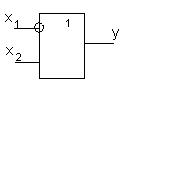
|
 y=x1→x2=x1+x2
y=x1→x2=x1+x2
| ||||||||
| Элемент реализует функцию компликация | 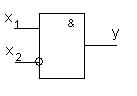
|
y= x1→x2=x1x2 | ||||||||
| Элемент реализует функцию эквиваленция | 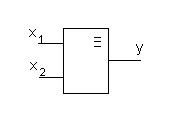
| y=x1~x2 | ||||||||
| Элемент реализует функцию сложение по модулю 2 | 
|
 y=x1 + x2 y=x1 + x2
| ||||||||
| Константа 0 | 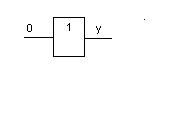
| y=0 | ||||||||
| Константа 1 | 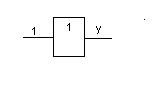
| y=1 |
Задание 5. Заданы логические функции: F1=∙ 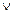 x2 ∙ x3 и
x2 ∙ x3 и
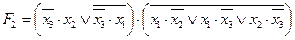 .
.
Требуется: a) получить кратчайшую форму записи функции F1 и F2;
б) проверить, являются ли они тождественными.
РЕШЕНИЕ
а) Функцию F1 упростить нельзя.
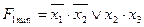
 =
= 
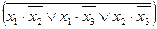 =
=
= 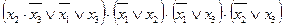 =
=
= 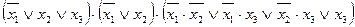 =
=
=  =
=
= 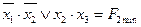
б) Функции F1 и F2 имеют одинаковую форму записи и тождественны.
Решить самостоятельно:
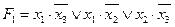
- Заданы логические функции: и
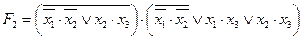
Путем тождественных преобразований получить минимальную форму записи функций и проверить, является ли функция F2 тождественной функции F1.
2. Заданы логические функции: F1=1 на наборах 2, 3, 5 и
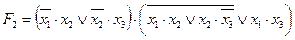 .
.
Путем тождественных преобразований получить минимальную форму записи функции F2 и проверить, является ли она тождественной функции F1.
3.Заданы логические функции: F1=0 на наборах 2, 3, 5 и
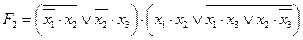 .
.
Путем тождественных преобразований получить минимальную форму записи функции F2 и проверить, является ли она тождественной функции F1.
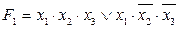
4. Заданы логические функции: и
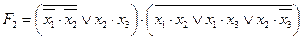 .
.
Путем тождественных преобразований получить минимальную форму записи функций и проверить, является ли функция F2 тождественной функции F1.
Задание 5. Логическая функция F(A,B,C) задана следующей таблицей истинности: F(A,B,C) = 9016
Построить ее функциональную схему, используя 4 элемента следующего базиса: константа 1, дизъюнкция, сложение по модулю 2.
9.5 Алгоритмизация
Задача.
Найти значение переменной S, вычисляемое в программе, написанной на алгоритмическом языке при следующих значениях исходных данных:
A=8769;
N=3;
Del=(1000,100,10,1);
| АлгСумма(арг цел A,арг целN,арг цел табdel[0:N],рез цел S) нач цел I,K,цел таб М[0:N], цел табR[0:N] нц дляIот 0 доN M[I]:=A/del[I]; A:=A-(A/del[I])*del[I]; кц нц дляKот 0 доN R[K]:=M[3-K]; кц S:=R[1]+R[3]; выводS кон | При выполнении задания учесть: операция / означает целочисленное частное, если делимое и делитель – целые числа. |
РЕШЕНИЕ:
Составим трассировочную таблицу.
Выполнение первого цикла со счетчиком I
| A | I | M[0] | M{1] | M[2] | M[3] |
| 8769/1000=8 | |||||
| 8769-8*1000=769 | |||||
| 769/100=7 | |||||
| 769-7*100=69 | |||||
| 69/10=6 | |||||
| 69-6*10=9 | |||||
| 9/1=9 | |||||
| 9-9*1=0 |
Итак, M=(8,7,6,9)
Выполнение второго цикла со счетчиком K
| K | R[0] | R{1] | R[2] | R[3] |
| M[3]=9 | ||||
| M[2]=6 | ||||
| M[1]=7 | ||||
| M[0]=8 |
Итак, R=(9,6,7,8).
Тогда S=R[1]+R[3]=6+8=14.
ОТВЕТ: S=14.
Задача 2. Найти значение переменной S, вычисляемое в программе, написанной на алгоритмическом языке при следующих значениях исходных данных:
M=(2,3,5,7);
N=3;
A=231;
| алгСумма(арг таб целM[0:N], арг целN,A, рез цел S) нач цел K S:=0; нц дляKот 0 доN если A mod M[K]<>0 тоS:=S+M[K]; кц выводS кон | При выполнении задания учесть: операция mod – остаток от деления, если делимое и делитель – целые числа. |
РЕШЕНИЕ:
Исполнение алгоритма.
Обозначим (1) проверяемое условие (A mod M[k]<>0)
| A | K | M[K] | (1) | S |
| нет | ||||
| да | S=0+3=3 | |||
| нет | ||||
| да | S=3+7=10 | |||
| -КЦ |
ОТВЕТ: S=10.
Выполнить самостоятельно.
1.Найти значение переменной S, вычисляемое в программе, написанной на алгоритмическом языке при следующих значениях исходных данных:
N=3;
Т=(( 6 6 6 5),( 2 5 3 3),( 7 5 3 2),( 7 5 7 1))
| алгСумма(арг целN,арг цел таб Т[0:3,0:3],рез целS) нач цел I, цел j, целтаб М[0:N] нц для I от 0до N S:=0; нц для J от 0 до I S:=S+T[I,J]; кц еслиS mod T[I,0]=0 тоM[I]:=S div T[I,0] иначе M[I]:=S mod T[I,0]; все кц S:=0; нц для I от 0 до N если T[I,I]>M[I] то S:=S+M[I] иначе S:=S-M[I]; все кц Кон | При выполнении задания учесть: · операция div означает целочисленное частное, а операция mod – остаток от деления, если делимое и делитель – целые числа. |
OTBET s=-3
2. Найти значение переменной S, вычисляемое в программе, написанной на алгоритмическом языке при следующих значениях исходных данных:
N = 3
U0 = 0
U1 = 1
| алгСумма(арг цел N, рез цел S) нач цел I,K,U, цел таб М[0:N] нц дляI от 0 до N U:=U0+U1; M[I]:=2*U; U0:=U1; U1:=U; кц S:=0; нц дляK от 0 доN S:=S+M[K]mod U; кц выводS кон | При выполнении задания учесть: операция mod – остаток от деления, если делимое и делитель – целые числа. |
Список литературы
I. Основная литература:
1. Соболь Б.В. и др. Информатика. (Учебник)., 2007, 3-е изд., 446с.;
2. Информатика и информационные технологии. (Учебное пособие) Под ред. Романовой Ю.Д., 2008, 3-е изд., 592с.;
3. Меняев М.Ф. Информатика и основы программирования. (Учебное пособие), 2007, 458с.;
4. Информационные технологии. (Учебник) Корнеев И.К., Ксандопуло Г.Н., Машурцев В.А. , 2007, 224с..
5. Савельев А. Я. Основы информатики. – Москва, «Издательство МГТУ имени Н.Э. Баумана», 2001
6. Малинин Л.А., Лысенко В.В. Основы информатики (учебник для вузов), М., изд-во «Феникс»,2006
7. Акулов О..П. , Медведев Н.А. Информатика. Базовый курс (учебник для вузов), М., изд-во «Омега», 2006
II. Дополнительная литература:
1. Архитектура компьютера. Таненбаум Э.С., 2007, 844с.;
2. Компьютерные сети. Принципы, технологии, протоколы. (Учебник) Олифер В.Г., Олифер Н.А. , 2006, 3-е изд., 958с.;
3. Организация ЭВМ. К. Хамахер, З. Вранешич, С. Заки, 2003, 5-е изд., 848с.;
4. Основы операционных систем. Курс лекций. Карпов В.Е., Коньков К.А., 2005, 536с.;
5. Языки программирования. (Учебное пособие) Голицына О.Л., Партыка Т.Л., Попов И.И. , 2008, 400с..
6. Р.Л. Хартли "Передача информации", в сб."Теория информации и ее приложения", М. Физматгиз, 1959.
7. А. Дегай "Сожмите свои данные", " Hard"n"Soft", № 4, апрель 1995.
8. И.В. Кузьмин, В.А. Кедрус " Основы теории информации и кодирования", Киев, В.Ш., 1997.
9. Тарасенко Ф.П. "Введение в курс теории информации", изд-во Томского университета, Томск, 1998.
– Конец работы –
Используемые теги: информатика0.031
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ИНФОРМАТИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?









Новости и инфо для студентов