Интегрируемость непрерывных и монотонных функций.

Th: Если f ограничена и монотонна на [a,b], то f Î L[a,b]:

Доказательство:

P = {a = x₀ < x₁< x₂ <...< x_n-1 < x_n = b}; h = b-a / n

M_K - sup f(x); m_K - inf f(x), где x Î [x+(k-1)h,x+kh]

x_K = a + kh D(x_K) = a + kh - (a + (k-1)h) = h

C(P)-c(P) = S_1...N(M_K-m_K)D(x_K) = S_1...N f(x_K)-f(x_K-1)D(x_K) = h[-f(a)+f(x₁)-f(x₁)+f(x₂)-...-f(x_K-1)+f(b)] = h(f(b)-f(a)) = b-a/n * [f(b)-f(a)] < E, так как b-a/n * [f(b)-f(a)]®0 при n®¥

Th:Если а непрерывна на [a,b], то f Î L[a,b]:

Доказательство:Wf(h) - supremum множества колебаний функции на каждом промежутке разбиения C(P)-c(P)=S_1...N (M_K-m_K)D(x_K) = h*S_1...N (M_K-m_K) £ h * n Wf(h) = (b-a) Wf(h) < E, так как при n®¥ Wf(h)®0.

 

14.Аддитивность интеграла. Замкнутость класса интегрируемых функций относительно арифметических действий и взятия модуля.

Th: Пусть a<b<c и fÎL[a,b]È[b,c], тогда fÎL[a,c] и=+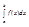

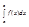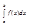
Доказательство:

P1 = {a = x₀ < x₁< x₂ <...< x_n-1 < x_n = b}; P2 = {b = y₀ < y₁< y₂ <...< y_n-1 < y_n = c}

C(P1) - c(P1) < E/2; C(P2) - c(P2) < E/2

P = P1ÈP2 = {a = x₀ < x₁< x_N-1 < b < y₁ <...< y_n-1 < y_n = c}

C(P) = C(P1) + C(P2), c(P) = c(P1) + c(P2) => C(P) - c(P) < E/2 + E/2 = E

Th: Пусть f, g Î L[a,b] A,B Î R тогда:

1) Af + Bg Î L[a,b]

2) fg Î L[a,b]

3) Если $ d>0 |g| ³ d, то f/g Î L[a,b]

4) |f| Î L[a,b] и || £ |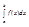

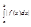
Доказательство:

2) C_FG(P) - c_FG(P) = S_1...N w_K(fg)D(x_K)

w_K(fg) = sup (f(x’)g(x’) - f(x’’)g(x’’), где x’, x’’ Î [x_K-1,x_K]

|f(x’)g(x’) - f(x’’)g(x’’)| = |f(x’)g(x’) - f(x’)g(x’’) - f(x’’)g(x’’) + f(x’)g(x’’)| =

= |f(x’)[g(x’) - g(x’’)] + g(x’’)[f(x’) - f(x’’)]| £ |f(x’)|w_Kg + |g(x'')|w_Kf £ Mfw_Kg + Mgw_Kf, где Mf - sup |f(x)|, Mg - sup |g(x)| - на [a,b]; w_Kg и w_Kf - колебания функций g(x) и f(x) на отрезке [x_K-1,x_K] соответственно;

Получили: S_1...N w_K(fg)D(x_K) £ S_1...N Mfw_KgD(x_K) + S_1...N Mgw_KfD(x_K)

Из интегр. f(x): $ такое P1: S_1...N w_KfD(x_K)<E/2*Mg, т.е. MgS_1...N w_KfD(x_K) =

= S_1...N Mgw_KfD(x_K) < E/2

Из интегрируемости g(x): $ такое P2: S_1...N w_KgD(x_K) < E/2 * Mf, т.е. MfS_1...Nw_KgD(x_K) = S_1...N Mfw_KgD(x_K) < E/2

Получили: $ P = P1ÈP2: S_1...NMfw_KgD(x_K) + S_1...NMgw_KfD(x_K) < E/2 +E/2 = E => S_1...N w_K(fg)D(x_K) < E => fg Î L[a,b]

1) Af Î L[a,b]

==

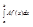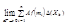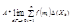
Из интегр. функции f следует lim S_1...Nf(m_I)D(x_K) = I => lim S_1...N Af(m_I)D(x_K) - $ и равен A*I => что Af тоже интегрируется на [a,b], так как это верно " A и " f (интегрируемой) => Bg - тоже интегрируется на [a,b]

Докажем что f+g также интегрируется на [a,b]:

h = dP = b-a / n

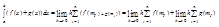
Оба предела в сумме сущ-ют так как функции f и g интегрируемы на [a,b], f сл-но сущ-ет lim hS_1...N (f(m_I) + g(m_I)) равный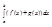=> f+g - интегрируема на [a,b] => сумма функций Af и Bg интегрируемых на [a,b] также интегрируется на [a,b].

4) |f(x’)| - |f(x’’)| £ |f(x’) - f(x’’)| £ w_K(f) => w_K(|f|) £ n_K(f)

Cf(P)-cf(P) < E (так как f интегрируется на [a,b]) и C|f|(P)-c|f|(P) £ Cf(P)-cf(P) => C|f|(P)-c|f|(P) < E => |f| также интегрируется на [a,b]

Pn, dP_N®0, M_N ПР midP_N

|sf(P_N,M_N)| = |S_1...N f(m_I)D(x_I)| £ |S_1...N| f(m_I)| D(x_I)| = |s| f|(Pn,Mn)| => lim |s f(Pn,Mn)| £

lim |s| f|(Pn,Mn)| => || £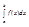

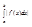
3) Докажем сначала что из интегрируемости g следует интегрируемость 1/g на том же промежутке при условии, что $ d>0: |g|³d:

|1/g(x’)-1/g(x’’)|=|g(x’)-g(x’’)|/|g(x’)g(x’’)|=w_K/(|g(x’)|*|g(x’’)|)£w_K/d²=>w_K(1/g)£w_K(g)/d²

Так как g интегрируема, то S_1...N w_K(g)D(x_K) < Ed² => 1/d² * S_1...N w_K(g)D(x_K) < E

S_1...N w_K(1/g)D(x_K) £ S_1...N w_K(g)/d²D(x_K) = 1/d²*S_1...N w_K(g)D(x_K) < E =>

lim S_1...N w_K(1/g)D(x_K)) £ 0

Так как w_K(1/g) > 0 lim S_1...N w_K(1/g)D(x_K) = 0 => 1/g - интегрируема на [a,b].