рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Понятие функции нескольких переменных
Реферат Курсовая Конспект
Понятие функции нескольких переменных
Понятие функции нескольких переменных - раздел Математика, МАТЕМАТИКА Функции Двух Переменных Пусть На Плоскости Хоу Имеется Некото...
Функции двух переменных
Пусть на плоскости ХОУ имеется некоторое множество точек D и каждой точке 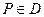 поставлено в соответствие по некоторому правилу число
поставлено в соответствие по некоторому правилу число 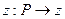 . Тогда говорят, что на множестве D задана функция
. Тогда говорят, что на множестве D задана функция 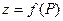 . Аргументом этой функции служит точка Р, пробегающая множество D, а значением – величина (переменная) z. Положение каждой точки Р определяется парой ее координат
. Аргументом этой функции служит точка Р, пробегающая множество D, а значением – величина (переменная) z. Положение каждой точки Р определяется парой ее координат 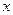 и
и 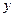 :
: 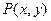 . Координаты этой точки независимы друг от друга и поэтому можно сказать, что задана функция
. Координаты этой точки независимы друг от друга и поэтому можно сказать, что задана функция 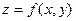 .
.
Определение. Переменная величина 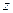 называется функцией двух независимых переменных
называется функцией двух независимых переменных 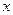 и
и 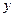 , заданной на некотором множестве D, если по некоторому закону или правилу каждой паре
, заданной на некотором множестве D, если по некоторому закону или правилу каждой паре 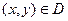 соответствует определенное значение
соответствует определенное значение 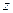 .
.
Пример. Пусть 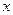 и
и 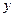 - длины сторон прямоугольника,
- длины сторон прямоугольника, 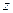 - его площадь. Тогда
- его площадь. Тогда 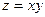 - функция двух независимых переменных
- функция двух независимых переменных 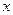 и
и 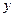 , заданная на множестве
, заданная на множестве 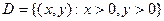 .
.
Пусть функция 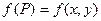 определена в некоторой области D, а точка
определена в некоторой области D, а точка 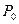 - либо точка этой области, либо граничная для D, в самой точке
- либо точка этой области, либо граничная для D, в самой точке 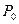 функция может быть не определена.
функция может быть не определена.
Определение. Число 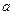 есть предел функции
есть предел функции 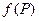 при
при 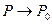 , если для любого
, если для любого  найдется
найдется 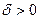 такое, что во всех точках Р области D, попавших в
такое, что во всех точках Р области D, попавших в  - окрестность точки
- окрестность точки 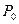 , выполняется неравенство:
, выполняется неравенство:
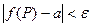 .
.
Пусть 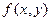 задана в области D и
задана в области D и 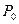 - внутренняя точка области D. Дадим аргументам
- внутренняя точка области D. Дадим аргументам 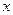 и
и 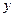 приращения
приращения  и
и  . Тогда
. Тогда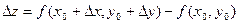 - полное приращение функции в точке
- полное приращение функции в точке 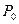 .
.
Условие непрерывности 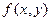 в точке
в точке 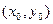 можно записать так:
можно записать так:
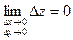 .
.
Функции трех переменных
Пусть D – некоторое множество точек в трехмерном пространстве 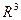 . Если каждой точке
. Если каждой точке 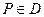 поставлено в соответствие по некоторому правилу число
поставлено в соответствие по некоторому правилу число 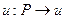 , то на множестве D задана функция
, то на множестве D задана функция 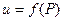 . Поскольку каждая точка Р определяется тремя координатами
. Поскольку каждая точка Р определяется тремя координатами 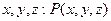 , то
, то 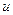 есть функция трех независимых переменных, заданная на множестве D:
есть функция трех независимых переменных, заданная на множестве D:
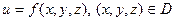 ,
,
где D – область определения функции 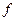 .
.
Пример. 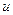 - объем параллелепипеда со сторонами
- объем параллелепипеда со сторонами 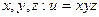 .
.
пусть задана функция 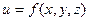 , тогда множество точек, в которых она принимает одно и то же значение С, называется поверхностью уровня. Ее уравнение :
, тогда множество точек, в которых она принимает одно и то же значение С, называется поверхностью уровня. Ее уравнение :
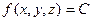 .
.
– Конец работы –
Эта тема принадлежит разделу:
МАТЕМАТИКА
бюджетного образовательного учреждения высшего... профессионального образования Московский государственный... университет экономики статистики и информатики МЭСИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Понятие функции нескольких переменных
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов