рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Приборостроение
- /
- Приборостроения и информатики
Реферат Курсовая Конспект
Приборостроения и информатики
Приборостроения и информатики - раздел Приборостроение, Министерство Образования Рф ...
Министерство образования РФ
Московская государственная академия
Приборостроения и информатики
Беланов А. С.
Физика
Часть IV
«Молекулярная физика и термодинамика»
«Элементы физики твердого тела, физики
атомного ядра и элементарных частиц»
Методическое пособие
Москва, 2003
УДК 53
Утверждено Ученым советом МГАПИ
28.10.2002г., протокол №10 в качестве учебного пособия
Рецензент – доцент, к.ф.-м.н. Попова Т. В.
Учебное пособие предназначено для студентов МГАПИ,
изучающих физику в течении 4-х семестров
Издательство МГАПИ
Физика, часть IV
В заключительной, четвертой части курса физики будет изучаться молекулярная физика и термодинамика, физика твердого тела и физика атомного ядра и элементарных частиц.
I. Молекулярная физика и термодинамика
Молекулярная физика и термодинамика изучают один и тот же круг явлений, а именно макроскопическиепроцессы в телах, т.е. такие явления, которые связаны с колоссальным количеством содержащихся в телах атомов и молекул. Но эти разделы физики, взаимно дополняя друг друга, отличаются различными подходами к изучаемым явлениям.
Последующее изучение молекулярной физики и термодинамики продемонстрирует эти подходы.
Лекция 1,2. Молекулярно-кинетическая теория
Основные положения молекулярно-кинетической теории
Число атомов и молекул в любом теле огромно. Например, в 1 м3 газа при обычных условиях содержится 1025 молекул, а в жидких и твердых телах 1028… Физические свойства макроскопических систем, состоящих из большого числа… Статистическийметод основан на использовании теории вероятностей и определенных моделей строения изучаемых систем. В…Уравнение состояния идеального газа
Идеальным называется газ, молекулы которого имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии. Оказывается при нормальных условиях, т.е. давлении Р0=1.013×105Па (что… Таким образом, многие газы можно считать с хорошим приближением идеальными.Следовательно, уравнение состояния для моля идеального газа имеет вид
Для произвольной массы m газа можно переписать уравнение (4) в виде РV=(m/M)RT или РV=nRT, (5) где n=m/M - число молей. Очевидно, чтоОсновное уравнение молекулярно-кинетической теории идеального газа
вернется в исходное состояние ( в центр куба) спустя время dt=(0.5l+0.5l)/v=l/v. В итоге получаем выражение для силы давления, оказываемого на… . (10) Если число молекул в сосуде N, то к cтенке А движетсяБарометрическая формула. Распределение Больцмана
Рассмотрим газ в сосуде (см. рис. 3). Если атмосферное давление на высоте h равно Р, то на высоте h+dh оно равно Р+dP (при dh>0 dP<0, т.к.… dP= -rgdh. (19) Воспользовавшись уравнением Клапейрона-Менделеева РV=RT , находим, что . Подставив это выражение в (19), получимЗакон Максвелла о распределении молекул идеального газа по скоростям
При выводе этого закона Максвелл предполагал, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии… Закон Максвелла описывается некоторой функцией f(v), называемой функцией… 1.6.1. Распределение Максвелла по модулю скорости молекулРаспределение Максвелла-Больцмана
(33) где - импульс частицы, в частности молекулы газа, - радиус-вектор,… Распределение (33) можно записать в виде распределения по полной энергии Е частицСреднее число столкновений и средняя длина свободного пробега молекул
Между двумя последовательными столкновениями молекулы проходят некоторое расстояние l, которое называется длиной свободного пробега молекул. Эти расстояния могут быть самыми разными. Поэтому в кинетической теории… При вычислении <l> необходимо принять определенную модель газа. Будем считать, что молекулы представляют собой…Тогда средняя длина свободного пробега молекул
<l>=<v>Dt/<z>=1/(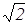 pd2n), (37)
pd2n), (37)
т.е. обратно пропорциональна концентрации молекул (или давлению P т. к., Р=nkT). Можно показать, что при нормальных условиях < l > ≈ 10-7 м и число столкновений за 1 секунду < z> /Dt≈1010 c-1.
Лекция 3. Явления переноса
Однако, беспорядочность теплового движения молекул газа, непрерывные столкновения между ними приводят к постоянному перемешиванию частиц и изменению… Эти потоки, характерные для неравновесных состояний газа, являются физической…Диффузия
Фик (1855 г) установил, что перенесенная масса dm через расположенную перпендикулярно направлению переноса вещества площадку dS^за время dt dm= - D(dr/dx) dS^dt,(1) где dr/dx характеризует скорость изменения плотности r на единицу длины x,Теплопроводность
dQ= -c(dT/dx) dS^dt, (3) где характеризует скорость изменения температуры Т на единицу длинны х, (греч.… (4)Внутреннее трение (вязкость)
Согласно закону Ньютона (1687 г) сила внутреннего трения между слоями газа (жидкости) , (5) где (du/dx) характеризует быстроту изменения скорости u на единицу длины x , S… Можно показать, что (6)Лекция 4,5. Физические основы термодинамики
Задачей термодинамического метода изучения состояний макроскопических систем является установление связей между непосредственно наблюдаемыми… Термодинамический метод, не связанный с модельными представлениями, обладает… Однако при термодинамическом рассмотрении остается нераскрытым внутренний (атомно-молекулярный) механизм явлений. По…Термодинамические системы. Равновесные состояния и равновесные процессы
Состояния любой термодинамической системы могут быть заданы с помощью ряда параметров, например, для газа P, V, T , для жидкости - a (коэффициент… Следует заметить, что не в любом состоянии системы все ее параметры имеют… Можно, например, представить себе систему, температура которой меняется от точки к точке, или газ, в разных точках…Внутренняя энергия идеального газа. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы
К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях. В курсе физики уже встречалось понятие числа степеней свободы i: это число… С учетом этого для одноатомных молекул газа (He, Ne, Ar …) i=3, для двухатомных молекул газа (H2, O2, N2 …) с жесткой…Работа и теплота
1. Путем совершения работы внешними телами над системой, например, при сжатии газа температура его повышается и, следовательно, изменяется… 2. Путем теплообмена, т.е. процесса обмена внутренними энергиями при контакте… Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия…Первое начало термодинамики (ПНТ)
Q=DU+A. (4) Уравнение (4) выражает ПНТ: теплота, сообщаемая системе, расходуется на… Для бесконечно малых процессов выражение (4) записывают в дифференциальной форме dQ=dU+dA или в более корректной…Работа газа при изменении его объема
РТеплоемкость
, Дж/(кгК). (9) Молярная теплоемкость – величина, равная количеству теплоты, необходимому для… , Дж/(мольК). (10)Применение ПНТ к изопроцессам
Изохорический процесс
Таким образом, . (14)Изобарический процесс
. (15) Молярная теплоемкость при постоянном давлении . (16)Изотермический процесс
совершение им работы против внешних сил: , (19) где n=m/M – число молей.Адиабатический процесс
Из ПНТ () для адиабатического процесса следует, что , (20) т.е. внешняя работа совершается за счет уменьшения внутренней энергии системы. Учитывая, что , найдем работу…Круговые процессы (циклы)
охватываемой замкнутой кривой. Если за цикл совершается положительная работа (цикл протекает по ходу часовой… Прямой цикл используется в тепловых двигателях – периодически действующих двигателях, совершающих работу за счет…Цикл Карно
Цикл Карно изображен на рис.8, где изотермическое расширение и сжатие заданы соответственно кривыми 1-2 и 3-4, адиабатическое расширение и сжатие –… Обратный цикл Карно положен в основу действия тепловых насосов. Тепловые…Энтропия
При изучении ПНТ () отмечалось , что dU является полным дифференциалом (из математики известно, что дифференциал dU называется полным, если интеграл… Из математики также известно, что величина, на которую надо умножать некоторое… Определенную таким образом функцию состояния S термодинамической системы называют энтропией, измеряется она в Дж/К. Из…Второе начало термодинамики (ВНТ)
Обобщение огромного экспериментального материала привело к необходимости формулирования второго, третьего и нулевого начал термодинамики. ВНТ в отличие от ПНТ не является всеобщим законом природы. Оно справедливо… 1. Невозможен процесс, единственным результатом которого является передача теплоты от холодного тела к горячему…Лекция 6. Реальные газы. Фазовые переходы
Силы и потенциальная энергия межмолекулярных взаимодействий
При r>>r0 они практически не взаимодействуют друг с другом. Введем понятие радиуса взаимодействия rВЗ, который определяют приближенно как… Известно, что существуют три основных агрегатных состояния вещества: газ, жидкость и твердое тело.Уравнение Ван-дер-Ваальса (ВдВ)
Остановимся на уравнении ВдВ (1873 г). Он внес в уравнение Клапейрона-Менделеева PV=RT две поправки. Первая поправка связана с действием сил отталкивания между молекулами. Она… P=RT/(V-b). (1)Изотермы Ван-дер-Ваальса
Левая, круто спадающая часть ее АВ соответствует жидкому состоянию, правая пологая часть FG – газообразному. Переход из жидкого состояния в… Ветви ВС и EF изображают метастабильные состояния вещества (т.е. относительно… С ростом температуры область горбов и впадин на изотерме ВдВ уменьшается и при температуре ТКР – критической…Фазы и фазовые переходы
Фазовый переход (фазовое превращение), в широком смысле – переход вещества из одной фазы в другую при изменении внешних условий (Т, Р, магнитных и… Различают фазовые переходы I рода и II рода. Фазовый переход I рода – широко… Фазовый переход II рода не сопровождается выделением или поглощением теплоты, плотность изменяется непрерывно, а…Фазовые диаграммы. Тройная точка
2) кривая плавления (КП) определяет условия равновесия между твердой и жидкой фазами (например, между льдом и водой); 3) кривая сублимации (КС)… Уравнение Клапейрона-Клаузиуса выражает связь наклона кривой равновесия двух… . (6)II. Элементы квантовых статистик и квантовой физики твердого тела
В последующих 4 лекциях будут изучаться тепловые и электрические свойства твердых кристаллических тел с использованием квантовой механики и квантовой статистики.
Лекция 7. Строение кристаллов. Элементы квантовой статистики
Кристаллическая решетка. Виды связей между частицами решетки
В зависимости от рода частиц, расположенных в узлах кристаллической решетки, и от характера сил взаимодействия между частицами различают 4… 1. Ионные кристаллы, например, NaCl. В узлах кристаллической решетки находятся… 2. Атомные кристаллы, например, С (алмаз), Ge, Si. В узлах решетки находятся нейтральные атомы, удерживающиеся там…Элементы квантовой статистики
Поведение этих частиц и квазичастиц описывается с использованием статистических методов, аналогично тому, как описывалось поведение молекул… Напоминаем, что задача статистики - указать распределение частиц по энергии Е,…Фермионы и бозоны. Распределение Ферми-Дирака и Бозе-Эйнштейна
К фермионам относятся электроны, протоны, нейтроны и все другие частицы, имеющие полуцелые проекции спина, т.е. LSZ=±(2n+1)/2 , где n=0, 1, 2 ... -… К бозонам относятся фотоны, некоторые ядра атомов, квазичастицы: фононы,… 7.3.1. ФермионыПонятие о вырождении системы частиц
, (6) где А=- параметр вырождения. (7) При А<<1 и ±1 в (6) можно пренебречь. В итоге получаемЛекция 8. Тепловые свойства твердых тел (кристаллов)
Классическая теория теплоемкости кристаллов. Закон Дюлонга и Пти
Простейшей моделью кристалла является правильно построенная кристаллическая решетка, в узлах которой помещаются атомы (или ионы, молекулы), принимаемые за материальные точки. Атом совершает тепловые колебания около положения равновесия. Если колебания малы, то они будут гармоническими. Энергия каждого атома слагается из потенциальной Wп и кинетической Wк. Известно [ cм. конспект лекций Физика, ч. I, лекции 11, 12 формулы (7), (8)], что в случае гармонических колебаний
Wп=(1/2) kA2cos2(wt+q)=(1/4) kA2[1+cos2(wt+q)], (1)
Wк=(1/2) kA2sin2(wt+q)=(1/4) kA2[1-сos2(wt+q)].
|
 Так как cos2(wt+q) c равной вероятностью принимают как положительные так и отрицательные значения и поэтому при усреднении обращается в нуль, то <WK>=<Wn>=(1/4)kA2.
Так как cos2(wt+q) c равной вероятностью принимают как положительные так и отрицательные значения и поэтому при усреднении обращается в нуль, то <WK>=<Wn>=(1/4)kA2.
В лекции 4 показано, что на каждую степень свободы приходиться в среднем кинетическая энергия (1/2)kT. Атом имеет 3 степени свободы, поэтому <WK>=<Wn>=(3/2)kT. Таким образом средняя энергия атома <Е>=<WK>+<Wn>=3kT. Умножив эту величину на постоянную Авогадро NA (число атомов в моле вещества), найдем внутреннюю энергию моля твердого тела
U=3kTNA=3RT, (2)
где R=kNA=8.31 Дж/мольК - универсальная газовая постоянная. Отсюда молярная теплоемкость твердого тела
C=dU/dT=3R»25 Дж/(моль×К). (3)
Этот закон был эмпирически (опытным путем) установлен в 1919 г. Дюлонгом и Пти. Он утверждает:
Молярная теплоемкость для всех простых твердых тел равна 3R, т.е.
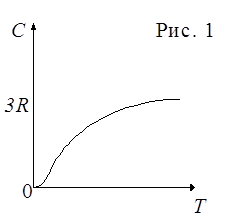 C=3R. (4)
C=3R. (4)
Для многих веществ этот закон хорошо выполняется, хотя некоторые вещества (алмаз С, Ве, В) имеют значительные отклонения от вычисленных теплоёмкостей. Опыт также показал, что С зависит от температуры и вблизи нуля кельвин для всех веществ С~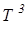 . На рис. 1 представлена характерная экспериментально полученная зависимость С от Т. Расхождение опытных и теоретических значений теплоёмкостей объяснили, исходя из квантовой теории теплоёмкости, Эйнштейн и Дебай.
. На рис. 1 представлена характерная экспериментально полученная зависимость С от Т. Расхождение опытных и теоретических значений теплоёмкостей объяснили, исходя из квантовой теории теплоёмкости, Эйнштейн и Дебай.
8.2 Понятие о квантовой теории теплоёмкости Эйнштейна и Дебая
Эйнштейн рассматривал кристалл как систему из N атомов, каждый из которых является квантовым гармоническим осциллятором (осциллятор - это физическая система, совершающая колебания). Колебания всех атомов происходят независимо друг от друга с одинаковой частотой n. Средняя энергия áЕñ, приходящая на одну степень свободы атома - гармонического квантового осциллятора:
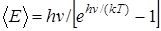 . (5)
. (5)
Внутренняя энергия моля твёрдого тела U = 3NAáEñ = 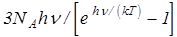 ,
,
отсюда молярная теплоёмкость твёрдого тела
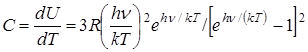 . (6)
. (6)
Этот результат качественно описывает зависимость С от Т, однако в области низких температур возникают расхождения с экспериментально полученными зависимостями С от Т.
Дебай развил теорию Эйнштейна. Он учёл, что:
1) колебания атомов в кристаллической решётке не являются независимыми и
2) основной вклад в энергию тепловых колебаний кристалла при низких температурах вносят колебания низких частот.
Таким образом, тепловое возбуждение твёрдого тела Дебай описал в виде упругих (звуковых) волн, распространяющихся в кристалле. Упругие волны в кристалле имеют квантовые свойства, проявляющиеся в том, что существует наименьшая порция - квант энергии волны с данной частотой n. Упругим волнам в кристалле сопоставляют фононы, обладающие энергией Е = hn. Фонон есть квант энергии звуковой (упругой) волны. Фононы являются квазичастицами, ведущими себя подобно микрочастицам. Заметим, что квазичастицы, в частности, фононы, не могут возникать и распространяться в вакууме, они существуют только в среде. Таким образом, квантование упругих волн привело к представлениям о фононах подобно тому, как ранее квантование электромагнитного излучения привело к представлению о фотонах.
Как указывалось в предыдущей лекции, фононы относятся к классу бозонов. Система бозонов описывается распределением Бозе-Эйнштейна (7.5). Для фононов m = 0 и ánñ =  , поэтому эта функция входила в формулы (5) и (6) данной лекции, с учётом того, что Е = hn.
, поэтому эта функция входила в формулы (5) и (6) данной лекции, с учётом того, что Е = hn.
Обозначим через dn число фононов с частотой в интервале от n до n+dn, тогда внутренняя энергия кристалла (вывод опускается)
 , (7)
, (7)
где nмакс = 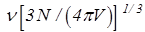 - максимальная частота фононов, N - число атомов в кристалле с объёмом V, v - скорость звука в кристалле, h, k - постоянные Планка и Больцмана.
- максимальная частота фононов, N - число атомов в кристалле с объёмом V, v - скорость звука в кристалле, h, k - постоянные Планка и Больцмана.
При вычислении U вводится характеристическая температура Дебая ТD = hnмакс/k и рассматриваются 2 предельных случая:
1.Высокие температуры Т>>TD (или kT>>hnмакс). При этом 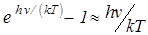 и
и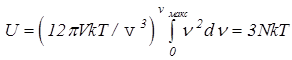 . Для одного моля N = NA и молярная
. Для одного моля N = NA и молярная
теплоёмкость С = dU/dT = 3NAk = 3R, т. е. соответствует закону Дюлонга и Пти.
2.Низкие температуры T<<TD . В этом случае при вычислении интеграла вводится новая переменная х = hn/(kT) и верхний предел заменяется на ¥:
 . (8)
. (8)
При выводе этой формулы было учтено, что интеграл равен 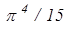 . Молярная теплоёмкость
. Молярная теплоёмкость
С = dU/dT =  , (9)
, (9)
т. е. пропорциональна 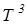 , что подтверждается на опыте. Таким образом, квантовая теория теплоёмкости Эйнштейна и Дебая объяснила теплоёмкость твёрдых тел.
, что подтверждается на опыте. Таким образом, квантовая теория теплоёмкости Эйнштейна и Дебая объяснила теплоёмкость твёрдых тел.
8.3. Теплоёмкость электронного газа в металлах
В металлах теплоёмкость складывается из теплоёмкости ионной решётки (см. параграф 8.2.) и теплоёмкости свободных электронов - электронного газа., т. е. С = Cреш + Сэл . Если бы электронный газ был невырожденный (классический), то каждый электрон обладал бы средней кинетической энергией (3/2)kT и средняя энергия электронного газа в одном моле металла была бы равна (3/2)kT×NA = (3/2)RT. Полная внутренняя энергия моля металла в этом случае была бы U = 3RT + (3/2)RT = (9/2)RT, а молярная теплоёмкость металла С = dU/dT = (9/2)R, т. е. в полтора раза больше теплоёмкости диэлектриков. Однако в действительности теплоёмкость металлов не отличается существенно от теплоёмкости неметаллических кристаллов.
Это противоречие устраняется квантовой теорией.
Средняя энергия теплового движения, равная » kT, составляет при комнатной температуре 1/40 эВ. Такая энергия может возбудить только малую часть электронов, находящихся на самых верхних энергетических уровнях, примыкающих к уровню Ферми. Энергия Ферми EF для хорошо проводящих металлов составляет » 6 эВ [см. (7.4) и комментарий этой формулы]. Действительно, расчёт показывает, что молярная теплоёмкость электронного газа
 ,
,
что примерно в 150 раз меньше теплоёмкости твёрдого тела С = 3R при Т = 300 К.
Относительный вклад теплоёмкости электронного газа в теплоёмкость металла будет увеличиваться с уменьшением Т, когда теплоёмкость С, пропорциональная 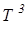 [см. (9)], уменьшается и она будет сравнима или даже будет меньше Сэл , которая пропорциональна Т.
[см. (9)], уменьшается и она будет сравнима или даже будет меньше Сэл , которая пропорциональна Т.
Таким образом, квантовая теория объяснила и теплоёмкость металлов.
Лекции 9,10. Электрические свойства кристаллов
Классическая электронная теория электропроводности металлов
Опыты, проведенные Рикке в 1901 г., Мандельштамом и Папалекси в 1913 г., Толменом и Стюартом в 1916 г. показали, что носителями тока в металлах являются электроны. Ток в металлах можно вызвать крайне малой разностью потенциалов. Это даёт основание считать, что электроны перемещаются по металлу практически свободно. Появление этих свободных электронов объясняется тем, что при образовании кристаллической решётки от атомов металлов легко отрываются слабее всего связанные валентные электроны. Можно показать, что концентрация их достигает 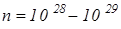 электронов в
электронов в  . При такой высокой концентрации электронов средняя сила, действующая на электрон со стороны всех остальных электронов и ионов, равна нулю и, следовательно, электроны можно считать свободными частицами и их взаимодействие с ионами можно рассматривать как ряд последовательных соударений.
. При такой высокой концентрации электронов средняя сила, действующая на электрон со стороны всех остальных электронов и ионов, равна нулю и, следовательно, электроны можно считать свободными частицами и их взаимодействие с ионами можно рассматривать как ряд последовательных соударений.
В этом приближении система электронов может анализироваться как система одноатомных молекул идеального газа. Исходя из этого, Друде и позднее Лоренц распространили результаты кинетической теории газов (см лекции 1,2) на свободные электроны - на так называемый электронный газ и получили законы Ома, Джоуля-Ленца в дифференциальной форме.
В позапрошлом семестре изучались эти законы [см. конспект лекций, ч. II, формулы (16), (38) в лекциях 6,7].
Плотность тока проводимости равна произведению удельной электрической проводимости проводника на напряжённость электрического поля в проводнике, т.е.
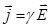 - закон Ома в дифференциальной форме. (1)
- закон Ома в дифференциальной форме. (1)
Удельная тепловая мощность тока в проводнике равна произведению его удельной электрической проводимости на квадрат напряжённости электрического поля в проводнике, т. е.
 - закон Джоуля-Ленца в дифференциальной форме, (2)
- закон Джоуля-Ленца в дифференциальной форме, (2)
где в (1) и (2) g - удельная электропроводность (g = 1/r).
Друде и Лоренц показали, что для металлических проводников
 , (3)
, (3)
где n - концентрация свободных электронов, e и m - заряд и масса электрона, álñ -средняя длина свободного пробега электрона, ávñ - средняя скорость теплового движения электрона. Согласно формуле (30) в лекции 1,2 ávñ  и при Т = 300 К, (масса электрона
и при Т = 300 К, (масса электрона  ),
), 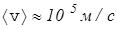 .
.
Скорость же направленного движения (скорость дрейфа электрона), возникающего благодаря электрическому полю  . Для
. Для  ,
, 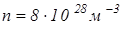 (заряд электрона
(заряд электрона  ), vдр = = 0,78 мм/с, т. е. много меньше скорости теплового движения электрона.
), vдр = = 0,78 мм/с, т. е. много меньше скорости теплового движения электрона.
Итак, классическая теория объяснила законы Ома, Джоуля-Ленца, Видемана-Франца. Вместе с тем она имеет ряд недостатков.
Строгий анализ с использованием квантовой теории показал, что не все валентные электроны свободно движутся по решётке с тепловыми скоростями, а лишь малая их часть. Подавляющее число валентных электронов в электропроводимости (как и в теплоёмкости) не участвуют. Это приводит к расхождениям между классической теорией и практикой. Например, из (3) следует, что 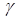 ~
~ 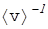 ~
~ 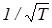 , а на практике в большом диапазоне изменения температур g ~ 1/Т.
, а на практике в большом диапазоне изменения температур g ~ 1/Т.
Эти и другие расхождения объясняет квантовая теория.
Понятие о квантовой теории электропроводности металлов
, (4) которая по внешнему виде напоминает классическую формулу (3). Здесь n -… Разгоняться в электрическом поле могут только электроны, энергия которых близка к уровню Ферми [см. лекцию 7], т. е. в…Элементы зонной теории кристаллов
По вертикали отложены значения энергии, по горизонтали ничего не отложено. Наинизший уровень или уровень с наименьшей энергией Е1 называется… Рассмотрим теперь N тождественных атомов, удалённых друг от друга настолько… Эта совокупность энергетических уровней, на которые расщепляется уровень изолированного атома, называется…Деление кристаллов на диэлектрики, металлы и полупроводники
Чтобы исключить тепловое движение будем сначала предполагать, что температура кристалла равна 0 К. По принципу Паули на каждом уровне может… Вдиэлектриках валентная зона целиком заполнена. А лежащая выше зона… Рис. 3 б) в) …Собственная проводимость полупроводников
Т.к. средние числа заполнения электронами уровней зоны проводимости малы, то можно пренебречь единицей в (7.1). Учитывая все это, получаем <ni>»exp[-DE/(2kT)].Примесные полупроводники
Введение в полупроводник примесей сильно влияет на его электрические свойства. Рассмотрим, например, что произойдет, если в решетке германия (Ge -…P-n-переход
При контакте разных полупроводников происходит диффузия носителей тока - электронов или дырок - из области, где их…III Физика атомного ядра и элементарных частиц
В двух последних лекциях курса общей физики будут изучены некоторые элементы ядерной физики. В основном будут излагаться опытные факты.
Лекция 11. Элементы ядерной физики
Строение атомных ядер
Итак, масса нейтрона mn=1,00867 аем или mn=939,6 МэВ, масса протона mp=1.00728 аем или mp=938,3 MэВ (масса электрона me=5,486×10-4 аем или… Заряд ядра Ze, где Z – порядковый номер элемента в периодической системе… Принято следующее обозначение ядер , где X – символ элемента. Например, , отсюда следует, что в ядре урана число…Дефект массы и энергия связи ядра
Dm=Zmp+(A-Z)mn-Mя. Прибавляя к первому слагаемому Zme и вычитая от последнего слагаемого Zme , где me – масса электрона, получим еще оду формулу для… Dm=ZmН+(A-Z)mn-Mа, (1) где mН – масса атома водорода, Mа- масса атома.Ядерные силы и их свойства
В настоящее время в природе известно четыре вида фундаментальных взаимодействий: сильное, электромагнитное, слабое и гравитационное. Сильное… Сильные и слабые взаимодействия – короткодействующие, т.е. они проявляются… Классическая физика полагала, что взаимодействие между телами передается с конечной скоростью посредством силовых…Радиоактивность
Ядра, подверженные радиоактивным превращениям называют радиоактивными, а не подверженные - стабильными. Большая часть радиоактивных ядер получена… Различают a - распад, b - распад и g - излучение. 1. При a - распаде из ядра вылетает a - частица (ядро атома гелия ):.Закон радиоактивного распада
N=N0exp(-lt), (2) где N0 – число нераспавшихся ядер в момент времени t=0; N – число… N0/2=N0exp(-lT1/2), отсюдаЯдерные реакции
Как правило, в ядерных реакциях участвуют два ядра и две частицы. Одна пара ядро-частица является исходной, другая пара – конечной. Символическая… Энергия ядерной реакции Q=с2[(mA+ma)-(mB+mb)]. Если (mA+ma)>(mB+mb), и… Тяжелые ядра при взаимодействии с нейтронами могут разделяться на две приблизительно равные части – осколки деления.…Лекция 12. Элементарные частицы и современная физическая картина мира
Элементарными частицами сейчас условно называют большую группу мельчайших микрочастиц, не являющихся атомами или атомными ядрами(за исключением…Взаимопревращаемость частиц
Среднее время жизни t частицы в свободном состоянии меняется в широких пределах: от 10-24с до бесконечности.Классификация элементарных частиц
Все частицы (в том числе и неэлементарные и квазичастицы) разделяются на бозоны и фермионы(об этом упоминалось уже в лекции 7).
Бозонами называются частицы или квазицастицы, обладающие нулевым или целочисленным спином. Бозоны подчиняются статистике Бозе-Эйнштейна. К бозонам относятся: гипотетический гравитон (спин=2), фотон(спин=1), промежуточные векторные бозоны (спин=1), глюоны (спин=1), мезоны и мезонные резонансы, а также античастицы всех перечисленные частиц.
Частицы или квазичастицы с полуцелым спином называются фермионами. Для них справедлив принцип Паули и они подчиняются статистике Ферми-Дирака. К фермионам относятся: лептоны (в число которых входят электроны), все барионы (в число которых входят и протоны, и нейтроны) и барионные резонансы, а также соответствующие античастицы. Для всех их спин равен ½.
По времени жизни t различают абсолютно стабильные, квазистабильные и резонансные частицы. Последние для краткости называют просто резонансами. Резонансными называют частицы, распадающиеся за счет сильного взаимодействия, с временем жизни 10-23с. Квазистабильные частицы (иногда их называют стабильные), время жизни которых превышает 10-20с, распадаются за счет электромагнитного или слабого взаимодействия. Время 10-20с, ничтожное в обыденных масштабах, считается большим, если его сравнивать с ядерным временем – временем, которое требуется свету на прохождение диаметра ядра (»10-15м), »10-23с. Абсолютно стабильными частицами являются, по-видимому, только фотон g, электрон е, протон р (в последнее время возникли сомнения в стабильности протона), электронное нейтрино nе, мюонное nm и таонное nt нейтрино и их античастицы – распад их на опыте не зарегистрирован.
Классификация частиц приводится в учебниках и с нею любознательный студент может ознакомиться самостоятельно.
Античастицы
Например первая античастица – позитрон (антиэлектрон) была обнаружена в 1935 г., его заряд равен +е. В вакууме позитрон столь же стабилен, что и… В 1955 г. были открыты антипротоны. Антипротоны отличается от протона р знаком… В 1956 г. были обнаружены антинейтроны. Антинейтрон отличается от нейтрона n знаком собственного магнитного момента.…Кварки
В 1964 г. Гелл-Манн и независимо от него Цвейг выдвинули гипотезу, подтвержденную дальнейшими исследованиями, что все элементарные частицы, участвующие в сильном взаимодействии (их относят к классу адронов) построены из трех более фундаментальных частиц, которые по предположению Гелл-Манна были названы кварками (Цвейг их назвал тузами). Три сорта кварков были обозначены буквами u (от англ. up – вверх), d(от англ.down – вниз), s(от англ. strange – странный). Предполагается, что кварки имеют дробный электрический заряд, равный е/3, т.е. меньше заряда е, который раньше считался элементарным (минимальным). Позднее были установлены еще три кварка: очарованный с, красивый или прелестный b и истинный t кварк. Этим 6 кваркам соответствует 6 антикварков.
В заключение отметим, что за последние 25-30 лет в физике элементарных частиц произошли революционные открытия, которые приближают к созданию теории Великого объединения – теории, которая объединит 4 типа взаимодействия (сильное, электромагнитное, слабое и гравитационное) в одно взаимодействие с единой природой всех сил. В настоящее время уже создана теория, в которой электромагнитное и слабое взаимодействия объединены в единое электрослабое взаимодействие. Создание теории Великого объединения является главной проблемой современной физики.
ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО ФИЗИКЕ, ЧАСТЬ IV
1. Основные положения молекулярно-кинетической теории (1.1).
2. Уравнение состояния идеального газа (1.2).
3. Основное уравнение молекулярно-кинетической теории идеального газа (1.3).
4. Молекулярно-кинетическое толкование термодинамической температуры. Средняя квадратичная скорость (1.4).
5. Барометрическая формула. Распределение Больцмана (1.5).
6. Закон Максвелла о распределении молекул идеального газа по скоростям (1.6, 1.6.1).
7. Вероятная, средняя арифметическая и средняя квадратичная скорости (1.6.1, 1.4).
8. распределение молекул по кинетическим энергиям. Распределение Максвелла-Больцмана (1.6.1, 1.7).
9. Среднее число столкновений и средняя длина свободного пробега молекул (1.8).
10. Явление переноса. Диффузия (3, 3.1).
11. Явление переноса. Теплопроводность (3, 3.2).
12. Явление переноса. Внутреннее трение (вязкость) (3, 3.2).
13. Физические основы термодинамики. Термодинамические системы. Равновесные состояния и равновесные процессы (4.1).
14. Внутренняя энергия идеального газа. Число степеней сводобы молекулы. Закон равномерного распределения энергии по степеням свободы (4.2).
15. Работа и теплота. Первое начало термодинамики (4.3, 4.4).
16. Работа газа при изменении его объема. Теплоемкость (4.5, 4.6).
17. Применение ПНТ к изохорическому и изобарическому процессам (4.7.1, 4.7.2).
18. Применение ПНТ к изотермическому и адиабатическому процессам (4.7.3, 4.7.4).
19. Круговые процессы (циклы) (4.8).
20. Цикл Карно (4.9).
21. Энтропия в термодинамике (4.10.1).
22. Энтропия с кинетической точки зрения. Третье начало термодинамики (4.10.2).
23. Энтропия в равновесной статистической физике. Второе начало термодинамики (4.10.3, 4.11).
24. Силы и потенциальная энергия межмолекулярных взаимодействий (6.1).
25. Реальные газы. Уравнение Ван-дер-Ваальса (6.2).
26. Изотермы Ван-дер-Ваальса (6.3).
27. Фазы и фазовые переходы (6.4).
28. Фазовые диаграммы. Тройная точка (6.5).
29. Кристаллическая решетка. Виды связей между частицами решетки (7.1).
30. Элементы квантовой статистики (7.2).
31. Фермионы, распределение Ферми-Дирака (7.3, 7.3.1).
32. Бозоны, распределение Бозе-Эйнштейна (7.3, 7.3.2).
33. Понятие о вырождении системы частиц (7.4).
34. Классическая теория теплоемкости кристаллов. Закон Дюлонга и Пти (8.1).
35. Понятие о квантовой теории теплоемкости Эйнштейна и Дебая (8.2).
36. Теплоемкость электронного газа в металлах (8.3).
37. Классическая электронная теория электропроводности металлов (9.1).
38. Понятие о квантовой теории электропроводности металлов (9.2).
39. Элементы зонной теории кристаллов (9.3).
40. Деление кристаллов на диэлектрики, металлы и полупроводники (9.4).
41. Собственная проводимость полупроводников (9.5).
42. Примесные полупроводники (9.6.1, 9.6.2).
43. p-n-переход (9.7).
44. Понятие о сверхпроводимости (9.8).
45. Строение атомных ядер (11.1).
46. Дефект массы и энергия связи ядра (11.2).
47. Ядерные силы и их свойства (11.3).
48. Радиоактивность (11.4).
49. Закон радиоактивного распада (11.5).
50. Ядерные реакции (11.6).
51. Элементарные частицы, взаимопревращаемость частиц (12, 12.1).
52. Классификация элементарных частиц (12.2).
53. Античастицы (12.3).
54. Кварки. Проблемы современной физики (12.4).
При написании конспекта лекций использовались известные учебники по физике, изданные в период с 1923 г. (Хвольсон О.Д. «Курс физики») до наших дней (Детлаф А.А., Яворский Б.М., Савельев И.В., Сивухин Д.В., Трофимова Т.И., Суханов А.Д., и др.)
[SK1]
[SK2]
– Конец работы –
Используемые теги: боростроения, информатики0.05
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Приборостроения и информатики
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов