Учебно-методический комплекс

Учебно-методический комплекс

Направление подготовки: «Химия»   Автор: доктор тех.наук, профессор Бубнов В.А.

Учебный план

Семестр I

План лекционных занятий

 

План лабораторных работ

   

Домашние задания

 

Домашнее задание №1

Линейная алгебра

Задание 1 Корень уравнения равен …   Варианты ответа 1. 1,5 2. 6 3. – 1,5 4. – 6

Решение:

Определитель второго порядка вычисляется следующим образом:
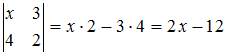. По условию задачи определитель равен нулю, то есть 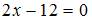. Следовательно, .

 

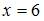Задание 2

Даны матрицы 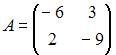и 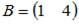. Тогда …
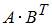Варианты ответа

1. не существует, т.к. матрицы в данном порядке умножать нельзя

2. равно

3. равно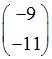

4. равно

Решение:

Умножаем первую матрицу на транспонированную вторую:
.

 

Задание 3

Матрица, обратная матрице , найденная с помощью элементарных преобразований, имеет вид …

Задание 4

Определитель 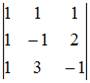после приведения к треугольному виду можно записать как …

 

Задание 5

Если 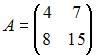, то обратная к ней матрица 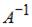равна …

 

 

Задание 6

Если выполняется равенство 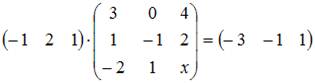, то значение х равно …

 

Задание 7

Система линейных уравнений 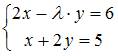не имеет решений, если 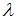равно …

 

Задание 8

Дана матрица . Тогда обратная матрица 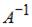равна …

 

Задание 9

Пусть клеточные матрицы А и В имеют вид: 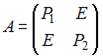, , 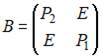где 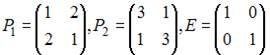. Тогда сумма матриц А и В равна…

 

Задание 10

Все значения , при которых столбцы матрицы 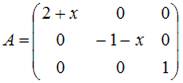линейно независимы, образуют множество …

Задание 11

Пространство есть прямая сумма подпространств…

Задание 12

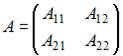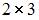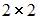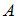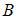Даны клеточные матрицы и . Размерность блоков – , – . Если произведение клеточных матриц и существует, то число строк в блоках 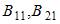равно…

 

Задание 13

Система линейных однородных уравнений 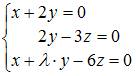имеет бесконечное число решений при 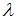, равном …

 

Задание 14

Если ранг матрицы 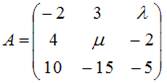равен рангу матрицы 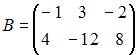, то разность 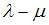равна …

 

Задание 15

Ранг матрицы равен …

 

системы линейных уравнений методом Крамера можно представить в виде …

 

Задание 16

Дана система линейных уравнений , определитель матрицы которой 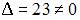. Если ее решение , , 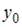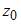найдено по формулам Крамера, где , то значение выражения 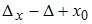равно …

Домашнее задание №2

«Теория множеств»

Задание 1. Теоретико-множественные методы обработки информации

Задача 1. Заданы множества А={f,b,c,h,g,e,n} и B={b,c,d,e,f,g,h}. Является ли одно из них подмножеством другого?

Ответ: Множества не являются подмножествами одно другого.

 

Задача 2. Заданы множества 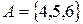и 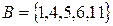. Является ли одно из них подмножеством другого?

Ответ: Множество А есть подмножество множества В.

 

Задача 3. Заданы множества А={ Все студенты г. Москвы } и B={ Все студенты МГПУ}. Является ли одно из них подмножеством другого?

Ответ: Множество В является подмножеством множества А.

 

Задача 4. Множество А=. Каким числовым множеством является множество А?

Ответ: Множеством R действительных чисел (Числовой осью).

 

Задача 5. Заданы множества A = 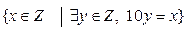и B = 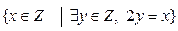.Является ли одно из них подмножеством другого?

Ответ: Множество А является подмножеством множества В.

 

Задача 6. Заданы множества А ={a, b, c, d, m, n, x} и B ={a, b, x, e, f, g, h}.Какое множество C будет являться пересечением множеств А и В?

Ответ: C = {a, b, x}.

 

Задача 7. Даны множества C={ a, b, c, d, e} и D={c, d, e, f, g, h}. Какие элементы будет содержать множество CD?

Ответ: {a, b}

 

Задача 8. Даны множества C={ a, b, c, d, e} и D={c, d, e, f, g, h}. Какие элементы будет содержать множество DC?

Ответ: {f, g, h}

 

Задача 9. Даны множества C={ a, b, c, d, e} и D={c, d, e, f, g, h}. Какие элементы будет содержать множество CD?

Ответ: {a, b, c, d, e, f, g, h}

 

Задача 10. Даны множества C={ a, b, c, d, e} и D={c, d, e, f, g, h}. Какие элементы будет содержать множество C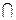D?

Ответ: {c, d, e}

 

Задача 11. Пусть 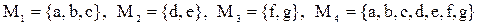. Как можно получить множество M_1, используя операции над множествами M₂, M₃, M₄ ?

Ответ: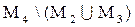

 

Задача 12. Заданы множества А ={3, 4, 5, 7, 9} и B ={1, 3, 5, 7, 11}. Какие элементы будет содержать множество C = A∩( B A) ?

Ответ: С = Ø (Множество С будет пустым множеством, т.е. не будет содержать ни одного элемента).

 

Задача 13. Заданы множества А={3, 4, 5, 7, 9} и B={1, 3, 5, 6, 7, 11}. Какое множество описывает закрашенная фигура в следующей диаграмме Венна (Рис.1)?

 

Ответ: C = {4, 9}

 

Задача 14. Заданы множества N= {1,2,3,4,5,7,8,9,11}, А={3,7,9} и B={1,3,5,7,11}.Какое множество описывает следующая диаграмма Венна:

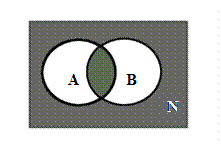· С = {1,2,3,4,5,7,8,9,11,}.

· С = {2,4,8}

· C = {2,3,4,7,8}

· C = {1,3,5,7,9,11}.

· C = {2,4,8,9}

Ответ №3

 

Задача 15. Заданы множества N= {1,2,3,4,5,6,7,8,9,11,13}, А={3,7,9} и B={1,3,5,7,11}.Какое множество описывает следующая диаграмма Венна:

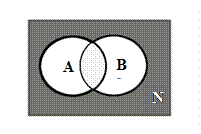· С = {1,2,3,4,5,6,7,8,9,11,13}.

· С = {2,4,6,8,13}

· C = {1,5,11}.

· C = {1,3,5,7,9,11}.

· C = {2,4,6,8,9,13}

Ответ №2

 

Задача 16. Заданы произвольные множества А, В и С. Расположите указанные справа множества так, чтобы каждое из них было подмножеством следующего за ним.

·

·

· ,

·

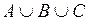
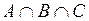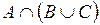
Ответ:. , , ,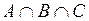

 

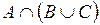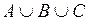
Задача 17. Отношение задано неравенством 4x+7y<0. Принадлежит ли пара чисел данному отношению принадлежит пара чисел (-1;1) данному отношению?

Ответ: Нет.

 

Задача 18. Отношение задано неравенством 4x+7y<0. Принадлежит ли пара чисел данному отношению принадлежит пара чисел (-2;1)) данному отношению?

Ответ: Да.

 

Задача 19. Отношение задано неравенством x²+y²<16. Какие пары чисел, являющиеся координатами точек плоскости, принадлежат данному отношению?

Ответ: пары чисел, являющиеся координатами точек плоскости внутри окружности с радиусом, равным 4, с центром в начале координат.

 

Задача 20. Заданы множества {1,-3} и 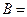{-а, в}. Какое множество является декартовым произведением множеств А´В ?

Ответ: {(1,-a), (1, в), (-3,-а), (-3, в)}.

 

Задача 21. Верно ли утверждение ?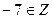

Ответ: да.

 

Задача 22. Верно ли утверждение ?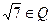

Ответ: нет.

Задача 23. Верно ли утверждение?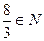

Ответ: нет.

 

Задача 24. Верно ли утверждение ?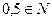

Ответ: нет.

 

Задача 25. Верно ли утверждение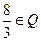

Ответ: да.

 

 

 

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

ОБЩЕИНСТИТУТСКАЯ КАФЕДРА ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН

ИНСТИТУТА МАТЕМАТИКИ И ИНФОРМАТИКИ ГОУ ВПО МГПУ

Технологическая карта

Примечание: · Каждое задание (1-10 пункты тех. карты) оценивается максимум в восемь… · Баллы по первым двум позициям выставляются лектором на зачете (экзамене).

Семестр II

План лекционных занятий

  Лекция №1 Понятие функции и особенности её поведения. Предел функции. Критерий Коши существования предела. Лекция…    

План лабораторных работ

   

Домашние задания

Домашнее задание №3

«Дифференциальное и интегральное исчисление»

 

Задача 1.Чему равна сума правой и левой производных функции 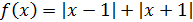в точке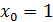

Решение.Данная функция не имеет производной в точке 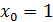. Поэтому в этом случае, вообще говоря, техника дифференцирования не может быть использована. Вычислим односторонние производные в заданной точке непосредственно, пользуясь соответствующими определениями.

Левая производная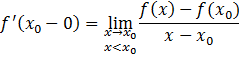

а правая производная

Вычислим значение левой производной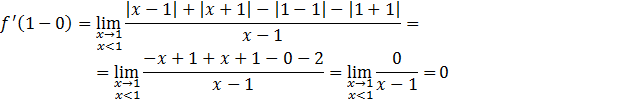

 

Вычислим значение правой производной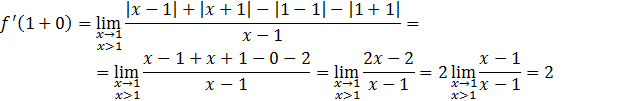

 

Таким образом, сумма односторонних производных равна .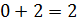

 

Задача 2.Чуму равен предел ?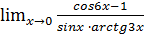

Решение.Здесь имеем неопределенность вида 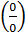. Подобного рода пределы можно вычислить с помощью первого замечательного предела и его следствий. При этом удобно применять эквивалентные бесконечно малые функции:

 

 

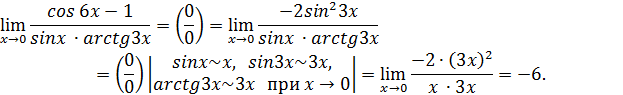
Задача 3.Чему равна производная функции ?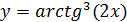

Ответ:

 

Задача 4.Чему равна производная первого порядка функции ?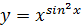

Ответ:

Ответ:

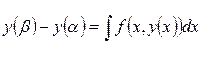Рассматриваемые методы приближенного интегрирования ДУ основаны на тождестве:

Пользуясь какой-либо квадратурной формулой для вычисления интеграла, получим различные формулы численного решения ДУ.

Метод Эйлера заключается в том, что интегральную кривую, проходящую через точку (х_оу_о), заменяют ломаной, каждое звено которой

проведено по направлению поля, определённого уравнением у' = f (х,у) в начальной точке этого звена. Иными словами, от предыдущей вершины ломаной к последующей двигаются по касательной к интегральной кривой, проведённой через начальную точку каждого звена.

Предположим, что нас интересует решение, отвечающее отрезку [х_о,b].

Разделим его на п равных частей

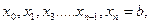
тогда ломаная Эйлера определится вершинами

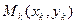(k= 0, 1, 2, ..., п),

где 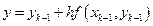, 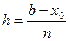- шаг деления,

 

Расчёт ведётся по следующей схеме:

k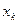
…..	…………	…………	………….	…………..
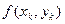
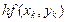
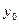
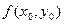
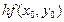
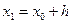
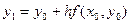
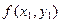
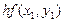
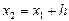
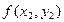
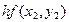
k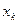
…..
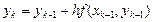
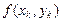
n-1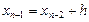
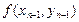
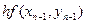
n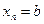

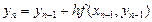
С увеличением числа делений, т.е. с уменьшением шага h, последовательность ломаных Эйлера как угодно близко приближается к искомой интегральной кривой. Но при этом увеличивается время вычислений и возрастает погрешность за счет ошибок округления. На практике задачу решают несколько раз, постепенно уменьшая шаг до тех пор, пока отклонения вычисленных значений функции для одних и тех же значений аргумента не станут пренебрежимо малы с точки зрения вычислителя.

 

Пример. Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 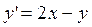, при начальном условии y(0)=0, шаг h = 0,1.

Ограничиться отысканием первых 10 значений y.

Ход работы.

1. Включите компьютер, нажмите кнопку Пуск , выберите программу Microsoft Excel.

2. В ячейку A1 введите значение 0.

3. Используя автозаполнение введите значения в ячейки А2 - А6.

 

 

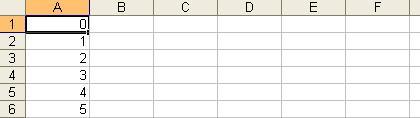
4. В ячейки В1 – Е1 введите заголовки :

5. В ячейку В2 введите значение Х_0.

6. В ячейку В3 введите формулу =B2+0,1 и далее продолжите автозаполнением до ячейки В11, заданный шаг h=0,1.

7. В ячейку С3 введите значение y_0.

8. В ячейку С3 введите формулу =C2+0,1*(2*B2-C2) и далее автозаполнением до ячейки С11.

9. В меню Формат ячейки, на вкладке Число выберите Числовой формат,и кол-во знаков после запятой 2. Щелкните ОК.

10. В ячейке D2 вводим: =2*B2-C2 и делаем автозаполнение до D10 .

 

 

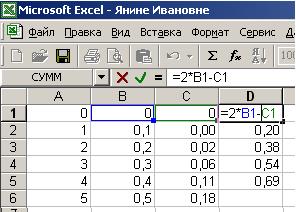
11. В ячейке E2 вводим формулу: =0,1*(2*B2-C2) и делаем автозаполнение до E10

12. Выбираем Формат - Диаграммы. Выберите тип График с накоплением и нажмите Далее.

13. Укажите диапазон от C2 до C11 и ряды в столбцах.

14. Далее выбираем вкладку Ряд. Введите в поле Подписи оси X промежуток от B2 до B11. Нажмите Далее.

15. Сделайте все необходимые подписи к диаграмме. Нажмите Далее.

16. Нажмите Готово.

 

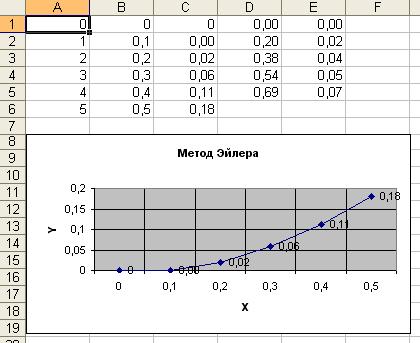
17.

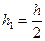Для повышения точности расчета уменьшим шаг вычислений. Выполните пп. 1-15 с заданным шагом

Вычисления проводить в ячейках, начиная с F1. Постройте график.

Найдем точное решение данного уравнения:

Данное уравнение является линейным неоднородным дифференциальным уравнением первого порядка.

Общее решение линейного однородного уравнения:

получается разделением переменных

Где С – произвольная постоянная.

Общее решение неоднородного уравнения находим, исходя из общего решения соответствующего однородного уравнения методом Лагранжа, варьируя произвольную постоянную, т.е. полагая:

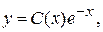где С(x) – некоторая, дифференцируемая функция от x.

Тогда искомое общее решение линейного неоднородного уравнения имеет вид:

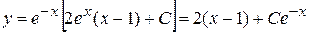
Используя начальное условие y(0) = 0, получим:

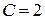
Следовательно, искомое частное решение имеет вид:

. (*)

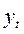График точного решения имеет вид:

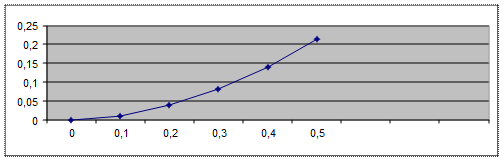Для построения графика точного решения в ячейку Е2 введите формулу (*), используйте автозаполнение. По данным столбца Е постройте график, сравните приближенное решение дифференциального уравнения с точным.

 

По таблице 1 сравните приближенное значение функции y с точным решением в зависимости от величины шага h.

 

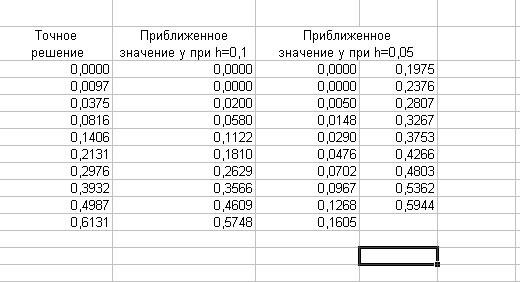
Таблица 1.

 

 

Задание

Задача 1. Используя метод Эйлера, найти значения функции y, определяемой дифференциальным уравнением 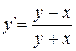, при начальном условии y(0)=1

шаг h=0,1; 0,05.

Задача 2. Методом Эйлера найти 10 значений функции y, определяемой уравнением y`=x+y, при начальном условии y(0)=1, полагая h=0,1; 0,05.

Задача 3. Методом Эйлера найти 10 значений функции y, определяемой уравнением 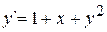, при начальном условии y(0)=1, полагая h=0,1; 0,05.

Задача 4.Методом Эйлера найти 10 значений функции y, определяемой уравнением 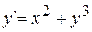, при начальном условии y(0)=0, полагая h=0,1; 0,05.

Задача 5. Методом Эйлера найти численное решение уравнения 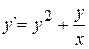при начальном условии y(2)=4, полагая h=0,1; 0,05.

Задача 6. Методом Эйлера найти численное решение уравнения на отрезке [0,1] при начальном условии y(0)=1, полагая h=0,2;0,1.

 

 

Лабораторная работа №10.