Абсолютно и условно сходящиеся ряды.

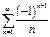Примеры. - сходится абсолютно. - сходится условно.

Рассмотрим произвольный ряд из комплексных чисел . Обозначим 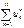- ряд, составленный из тех же чисел, взятых в другом порядке

Теорема 12.1. Если ряд - сходится абсолютно, то и - так же сходится и имеет ту же сумму.

Члены абсолютно сходящегося ряда можно переставлять.

Доказательство.

Обозначим , , .

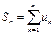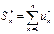Если исходный ряд сходится абсолютно, то $ - предел неубывающей последовательности частичных сумм .

Зафиксируем произвольное e>0. $ N_e:

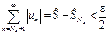Þ

Выберем такой большой номер M_e такой, что частичная сумма 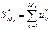содержала бы все слагаемые, что и . Для " m³M_e обозначим .

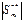не превышает суммы модулей своих слагаемых. Т.к. номера этих слагаемых больше, чем N_e, то все они содержатся в сумме Þ

.

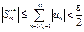Т.о. " m³M_e

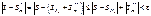
Þ$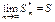т.е. .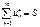

Замечание. Более того ряд 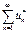сходится абсолютно.

Теорема Риммана. Если ряд 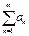, сходится условно, то " можно так переставить члены ряда, чтобы сумма его была бы равна A!!!

Доказательство.

В последовательности {a_n} есть как положительные, так и отрицательные члены. Выделим две подпоследовательности и . Обе имеют бесконечное число членов, т.к. если бы хоть одна из них состояла бы из конечного числа, это означало бы, что члены ряда 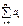не меняют знака, начиная в какого-то номера. Т.е. отбросив конечное число членов ряда 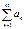, мы получим знакопостоянный ряд, сходимость которого эквивалентна абсолютной сходимости, а по условию теоремы ряд сходится условно.

Т.о. можно рассмотреть два знакоположительных ряда и . Оба они расходятся. Докажем это.

Рассмотрим частичные суммы

, , ,

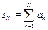Последовательность - расходится, а - сходится. Последние три последовательности состоят из положительных членов.

Пусть среди первых N членов ряда k положительных и m отрицательных, тогда

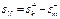
Т.к. 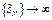, то хотя бы одно из слагаемых или так же стремится к бесконечности. Т.к. 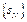- сходится, то обе и так же стремится к бесконечности, иначе бы их разность не могла бы стремиться к конечному числу.

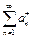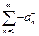Итак, оба рядаи расходятся. Тем ни менее члены обоих этих рядов стремятся к нулю, т.к. являются членами сходящегося ряда . Т.е. и .

Из членов условно сходящегося ряда составим ряд по следующему алгоритму:

Будем брать слагаемые из 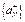до тех пор, пока частичная сумма ряда не превзойдет A. Частичные суммы рядабесконечно возрастает, поэтому рано или поздно они превысят выбранное нами A. Сразу в этот момент остановимся. Разность между частичной суммой и A при этом не превышает последнего слагаемого.

Далее будем брать слагаемые из 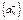до тех пор пока частичная сумма нашего ряда на станет меньше чем A. Это опять же рано или поздно произойдет, т.к. - расходится и следовательно его частичные суммы сколь угодно велики. Остановимся в тот самый момент когда сумма нашего ряда станет меньше, чем A. Разность между частичной суммой и A при этом не превышает последнего слагаемого.

Продолжая действовать подобным образом, мы получим ряд, составленный из членов исходного ряда, взятых в другом порядке. При этом частичные суммы этого ряда стремятся к A (их разность не превышает ). Т.о. наш ряд сходится к A.

Мораль.

От перемены мест слагаемых в бесконечная сумма не меняется, только если соответствующий ряд сходится абсолютно!!!